Восстановление функции по коэффициентам её ряда Фурье
Задание функции
Составляем модель для компьютерного эксперимента. В моей системе молекулы углекислого газа и плавиковой кислоты.
Связь H-F равна 0.9А, связь С=O - 1.2А.
Молекулы расположены на отрезке [0,30] (ангстремы). Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем. Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.
Для создания функции я использовала скрипт compile-func.py с параметрами
-g 9,1.1,11.1+1,0.6,12+8,1.3,16+6,1.4,17.2+8,1.3,18.4В итоге скрипт выдал текстовый файл.
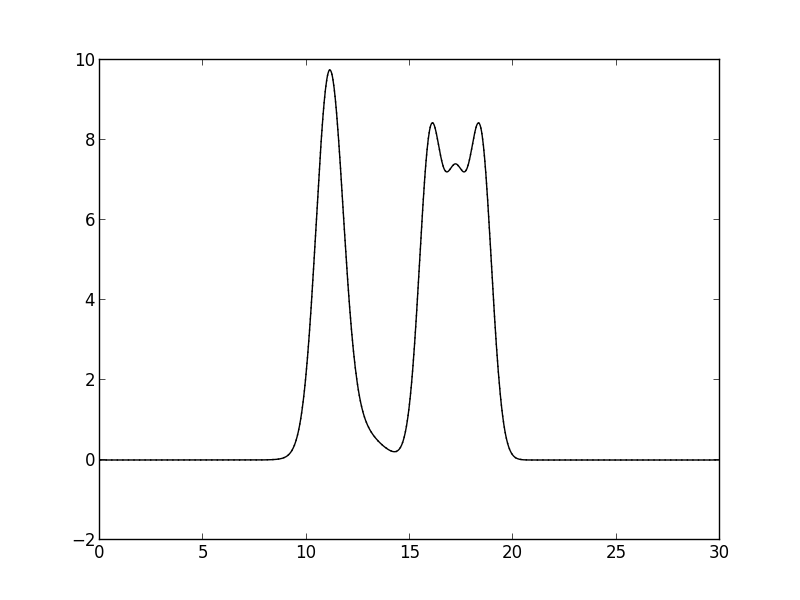
На рисунке 1 избражен график заданной функции электронной плотности. Как можно видеть, водород отдельным пиком не видно, а пик фтора искревлен.
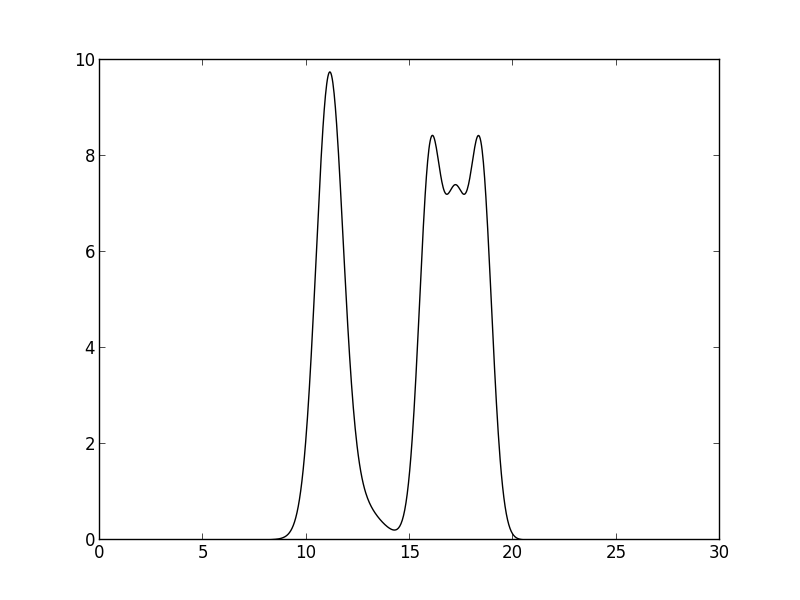
Рис. 1. График заданной функции ЭП.
Задача
Восстановить функцию ЭП по данным о амплитудах и фазах части ее гармоник Фурье. Амплитуды и фазы набора гармоник считаются полученными из экспериментов.Полные наборы гармоник
При помощи скрипта func2fourier.py я получила коэффициенты разложения функции в ряд Фурье (выходной файл, в нем приведены амплитуды и фазы гармоник, а также их номера.)Необходимо было найти n_0, при котором восстановление отличное.
Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"
Значение n_0 равно 30 (рисунок 2).
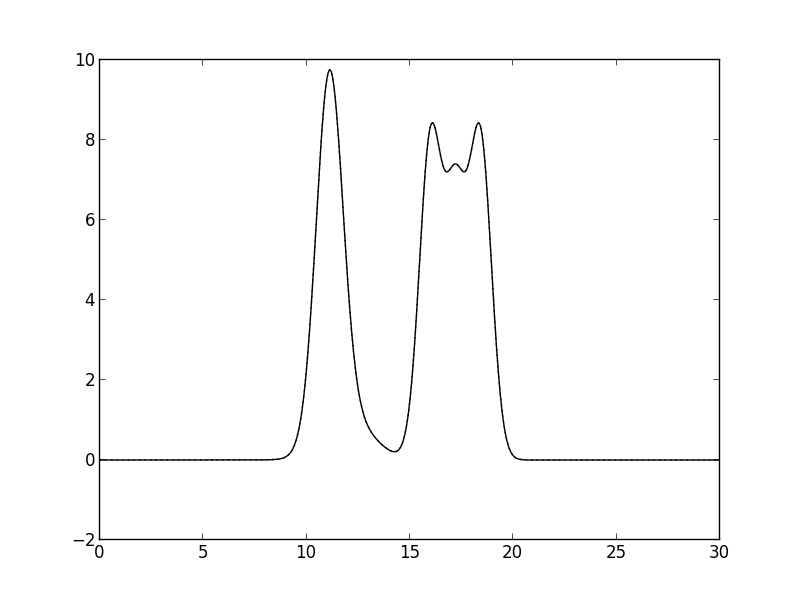
Рис. 2. n_0 равное 30. Ниже можно видеть графики для восстановленных функций по полным наборам гармоник для n, равных 2, 10, 15 и 20. (Сплошная линия - исходная электронная плотность, пунктирная линия - восстановленная электронная плотность)
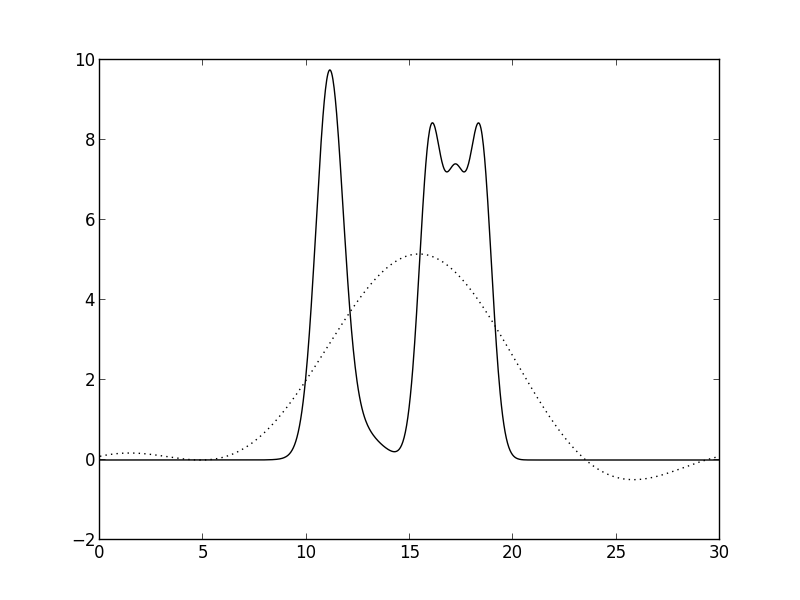
Рис. 3. n=2. Плохое восстановление.
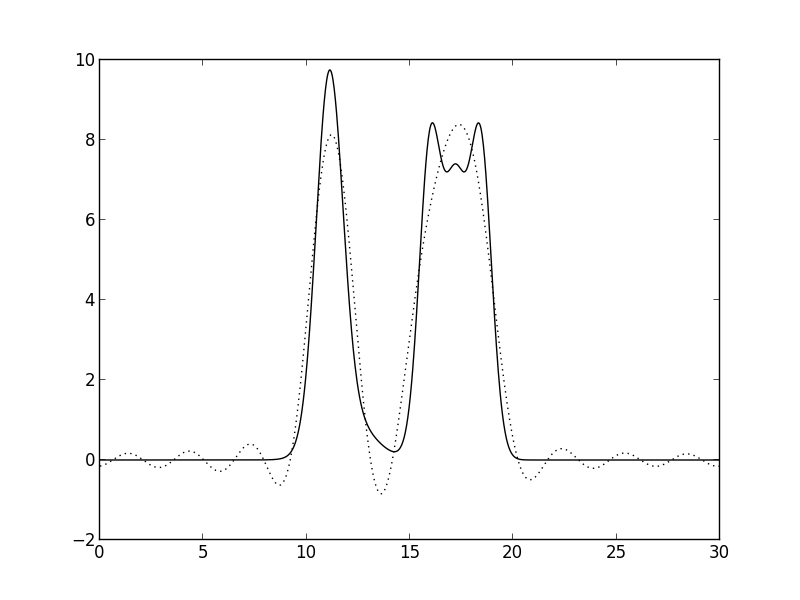
Рис. 4. n=10. Среднее восстановление.
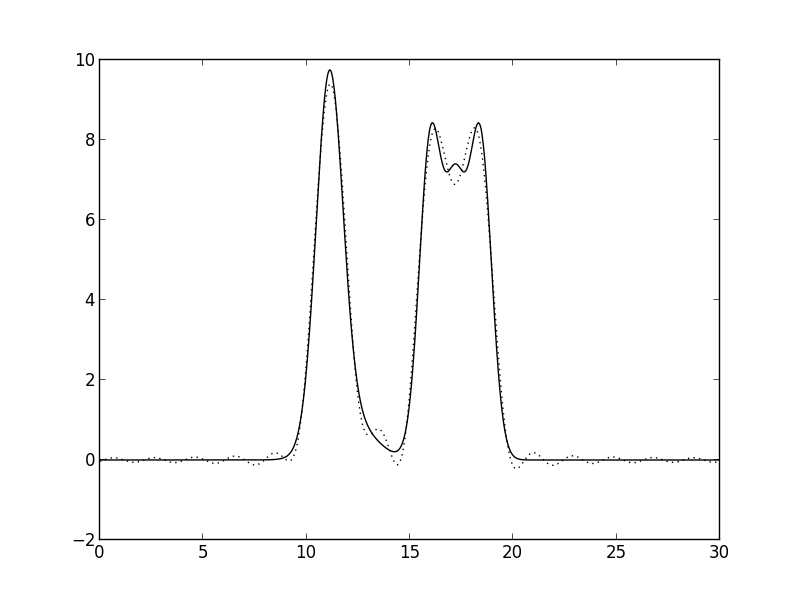
Рис. 5. n=15. Восстановление хорошее (водород не отличим от шума).
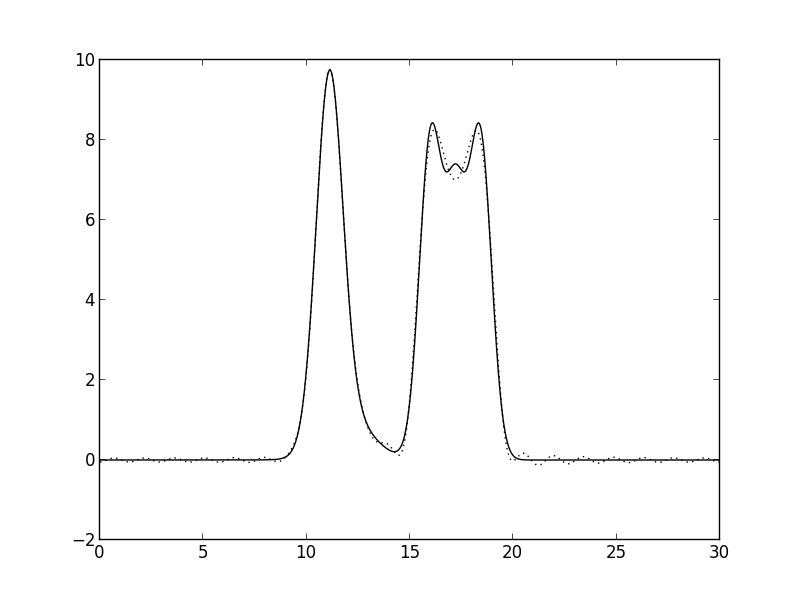
Рис. 6. n=20. Восстановление хорошее.
Затем к амплитудам и фазам был добавлен шум (10% к амплитуде и 10% к фазе). Восстановление функции по полному набору гармоник.
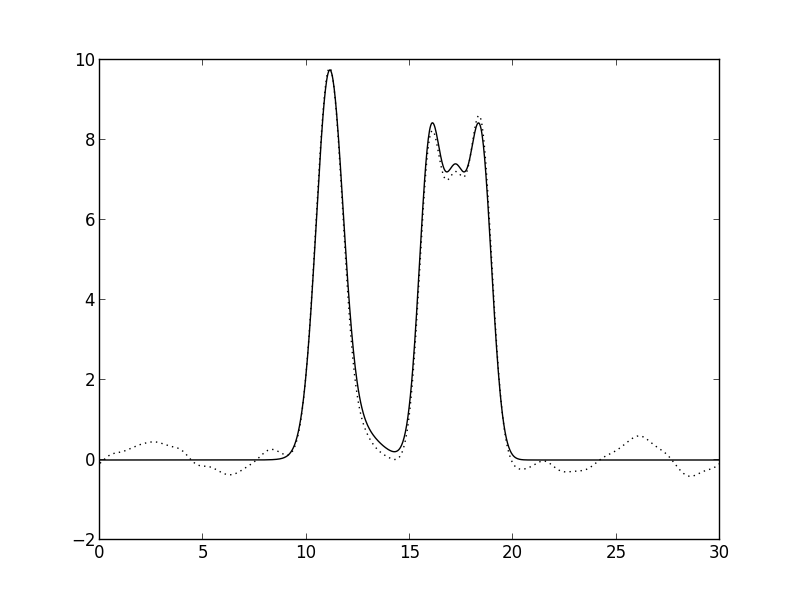
Рис. 7. P=10. Все пики, но пик водорода не отличим от шума. Хорошее восстановление.
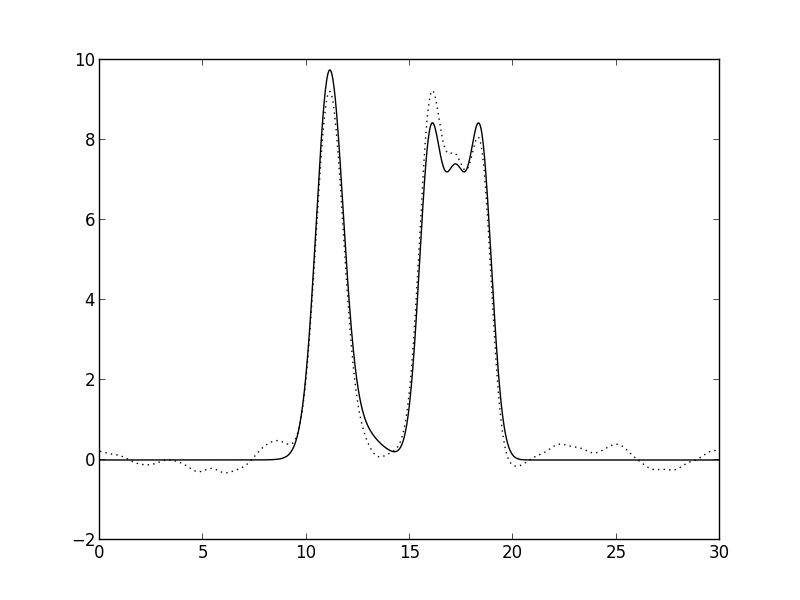
Рис. 8. F=10. Все пики есть, но пики водорода и углерода не отличимы от шума (Среднее восстановление).
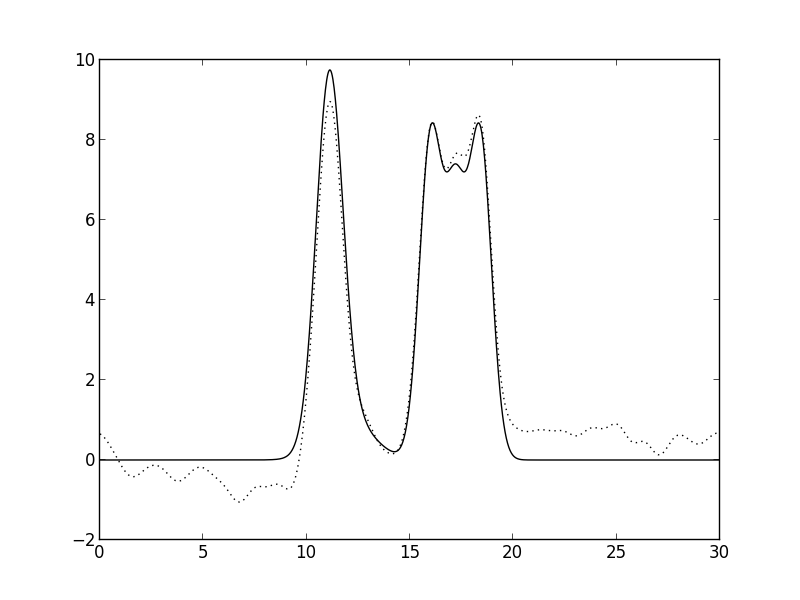
Рис. 9. P=10 и F=10. Восстановление хорошее.
Неполные наборы гармоник
Сначала необходимо удалить одну и две начальные гармоники (гармоника с номером 0; гармоники с номерами 0 и 1):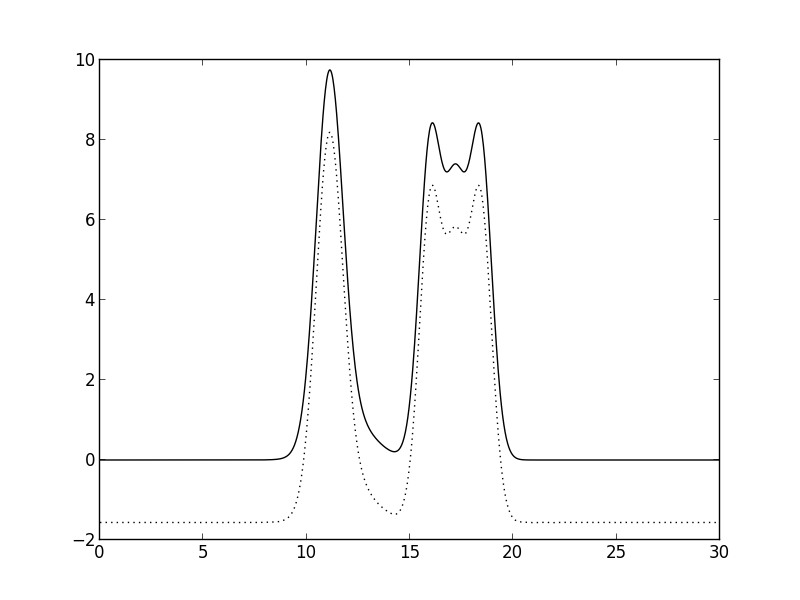
Рис. 10. Удаление гармоники с номером 0. График функции смещается, но восстановление отличное.
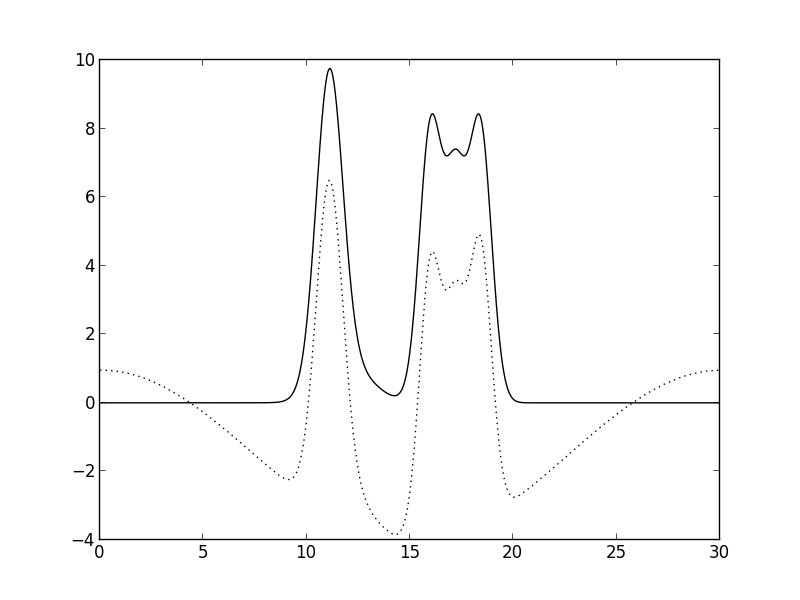
Рис. 11.Удаление гармоник с номерами 0 и 1. График функции исказился больше, однако все пики видны - хорошее восстановление.
Затем надо было удалить 10-15% гармоник из середины набора
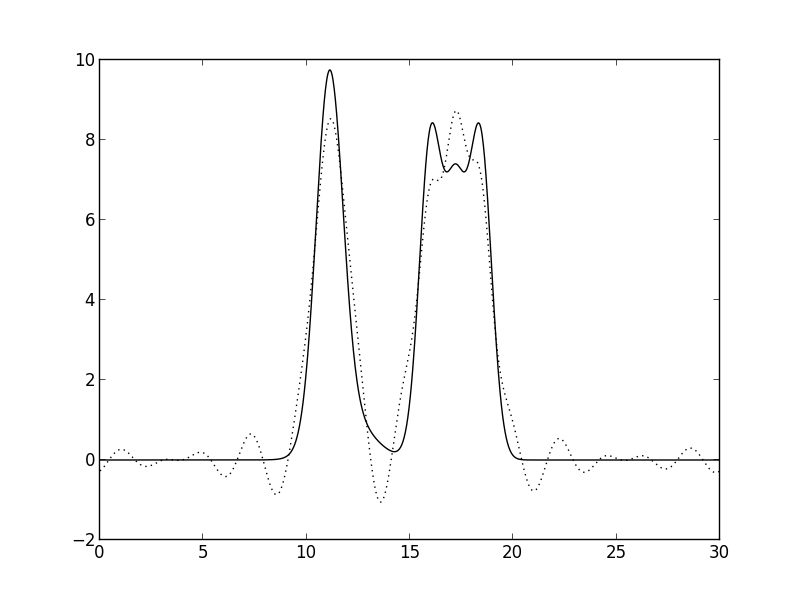
Рис. 12. Удаление 10% гармоник. В середине были удалены гармоники 11-13. Качество восстановления ухудшилось (хорошее восстановление). Сложнее различить атомы в молекуле углекислого газа.
Далее необходимо добивить одну гармонику с номером, превышающим n_0 на 10. Таким образом, добавляем гармонику 40.
 |  |
По результатам проделанной работы я заполнила таблицу.