Расчет значения энергии молекулы проводился в GAMESS
Зависимость энергии молекулы от длины С-С связи
Имеем на вход файл-заготовку: et.inp .
Есть скрипт для получения структур с различной длинной С-С связи, а затем их последующего обсчета. Заметим, что здесь длина С-С связи меняется в небольшом диапазоне
Как итог файл , в котоом записаны длина С-С связи и соответствующая этой длине величина энегии.
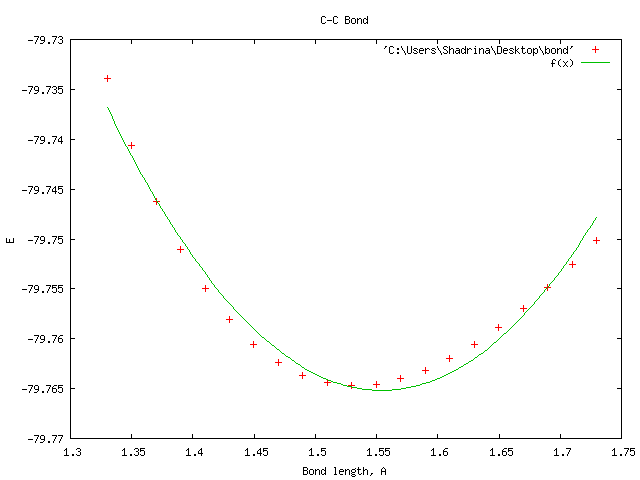
На графике показана зависимость Е от длины связи. Проведена аппроксимизация функцией: f(x)=a+k(x-b)^2. Получены значения:
a=-79,7652 +/- 0.0004522
k=0,563608 +/- 0,02335
b=1,55432 +/- 0,002455
Что можно сказать: в принципе так аппроксимизовать можно, но получается невполне точно. В последнем задании при увеличении шага изменения связи видно, что простого полинома 2 степени не достаточно. Хотя в узком диапазоне значений длины связи он работает
Зависимость энергии молекулы от величины ССН угла
Имеем на вход все ту же файл-заготовку: et.inp .
Теперь есть немного измененный скрипт: make_a.bash для получения структур с различным значением угла ССН( меняется от 109,2 - 113,2), а затем их последующего обсчета.
Как итог файл , в котором записаны углы и соответствующие величины энегии.
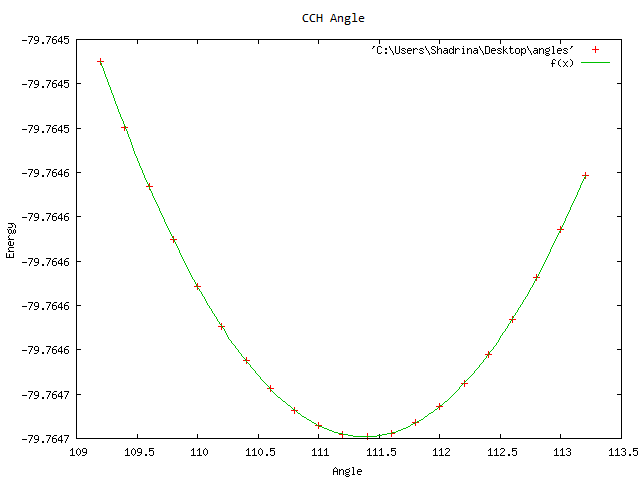
На графике показана зависимость Е от угла. Проведена аппроксимизация функцией: f(x)=a*x*x+b*x+c. (что-то в этот раз с помощью f(x)=a+k(x-b)^2 совсем не хотел аппроксимироваться) Получены значения:
a=3,56076e-005 +/- 6.227e-009
b=-0,00793195 +/- 1.385e-006
b=-79,3229 +/- 7,7e-005
Можно заметить, что здесь вообще хорошо аппроксимируется полиномом 2 степени.
Зависимость энергии молекулы от величины торсионного угла d3
Имеем на вход все ту же файл-заготовку: et.inp .
Теперь есть немного измененный скрипт: make_d3.bash для получения структур с различным значением торсионного угла( меняется от -180 до 180), а затем их последующего обсчета.
Как итог файл , в котором записаны углы и соответствующие величины энегии.
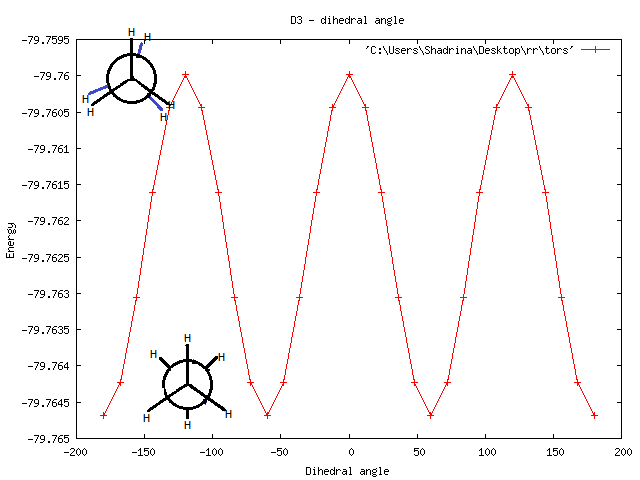
На графике показана зависимость Е от угла. Как видно у функции 3 max и 3 min (-180 и +180 одно и то же). Эти max и min соответствуют заслоненной и заторможенной конформациям. (так же показаны на рисунке)
А функция похожа на косинус с периодом 2/3 пи.
Зависимость энергии молекулы от длины связи С-С. Увеличенный диапазон значений
Есть скрипт для получения структур с различной длинной С-С связи: от 0,52 до 3,32.
Как итог файл , в котоом записаны длина С-С связи и соответствующая этой длине величина энегии. На графике показана зависимость Е от длины связи.
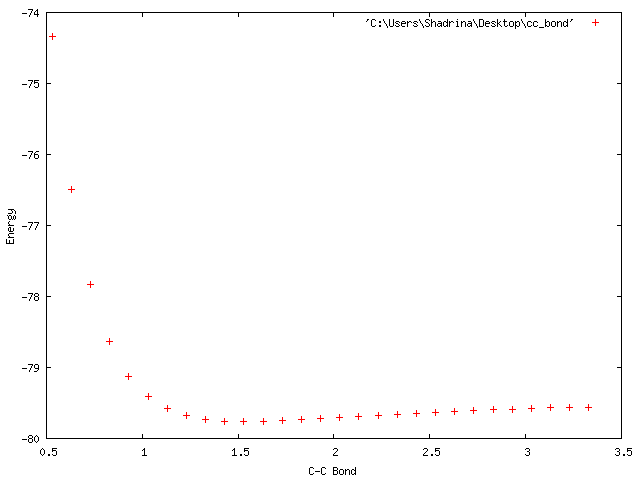
Как я провела аппроксимацию: в Excel по этим точкам пробовала провести линию тренда, выбирая из разных предложенных вариантов. Лучше всего подходили полиномы высокой степени. Мах, который я посмотрела, был 6 степени. Тогда в gnuplot я запустила аппроксимацию функцией: f(x)=a*x*x*x*x*x*x+b*x*x*x*x*x+c*x*x*x*x+d*x*x*x+e*x*x+f*x+g. Получила значения:
a = 0.508667689478983
b = -6.65658297842323
c = 35.4018762590522
d = -97.9037376994026
e = 148.599396823699
f = -117.528062696382
g = -41.8201200430358
Вот так у меня аппроксимировалось:
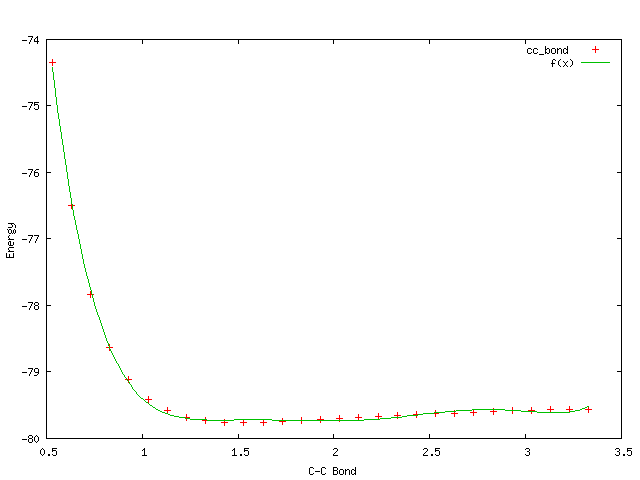
Видно, какую часть в самом первом задании мы пытались аппроксимиовать параболой - нижнюю, расположенную в районе обычного значения длины С-С связи: 1.54А. Только точки там были расположены кучнее.