Цель работы - исследовать восстановление функции Гаусса по коэффициентам ряда Фурье (с внесенным шумом).
Для исследования была выбрана функция гаусса для одномерной модели с 3 молекулами: H-C-O, H-O-C-S-C, C-N. Всего 10 атомов. Расстояния между атомами внутри молекул: 1-1.5 ангстрем, между молекулами: 3.5 (водородная связь O..H-O), 5 (гидрофобное взаимодействие C..C).
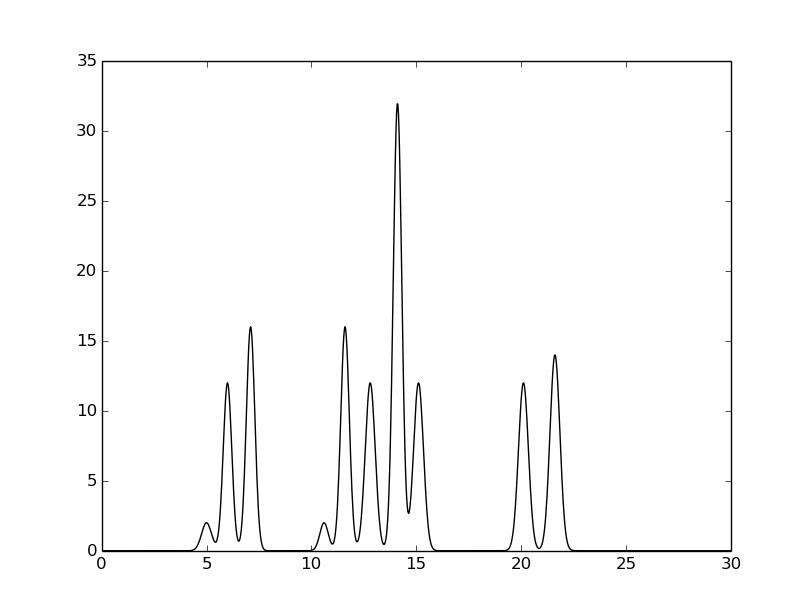
Для задания модели использовалась функция Гаусса: gauss = lambda*exp(-(beta^2)*(X-gamma)^2). Коэфициенты были подобраны так, чтобы величины пиков были пропорциональны количеству электронов в атомах (lambda параметр), расстояние между пиками - расстоянию между атомами (gamma параметр), ширина пика - порядка 1 (beta параметр).
Коэфициенты для модели: 2,3,5+12,3.5,6+16,3.5,7.1+2,3.5,10.6+16,3.5,11.6+12,3,12.8+32,3.5,14.1+12,3,15.1+12,3,20.1+14,3,21.6 - записаны в виде [lambda,beta,gamma+...].
Для вычислений использовались python скрипты и библиотека функций А.В.Алексеевксого, а также их модифицированные варианты. compile-func.py - принимает список коэффициентов, возвращает файл с поточечно заданной функцией Гаусса; func2fourier.py - принимает файл с поточечно заданной функцией Гаусса, возвращает файл с коэффициентами (гармониками) ряда Фурье, соответсвующего этой функции, есть опции зашумления по амплитуде или фазе; fourier-filter.py - позволяет удобно оставлять или исключать заданные номерами гармоники Фурье; fourier2func.py - восстанавливает функцию Гаусса по коэффициентам Фурье.
Этапы работы и результаты представлены в таблице. Иконка справа вызывает картинку, соответствующую строке таблицы. Черным цветом обозначена исходная функция Гаусса, красный пунктиром - восстановленная функция.
Ссылка на таблицу: .html
Формальные выводы из анализа:
- Гармоники порядка выше 100 никак визуально не проявляют себя на качестве реконструкции.
- При уменьшении количества гармоник (при сохранении полноты данныхи уменьшения разрешения) качество реконструкции падает: почти не заметно для 50-498, очень резко для 1-30.
- При заданных параметрах модели критическое значение n0, когда реконструкцию еще можно считать отличной, - 35 первых гармоник Фурье, разрешение 0.857 ангстрем.
- При уменьшении количества гармоник (при сохранении разрешения и уменьшении полноты данных, при удалении гармоник низкого разрешения,т.е. с малым индексом) качество реконструкции падает резко, и становится "чрезвычайно низким" при полноте данных меньше 90 %.
- При одновременном уменьшении полноты и разрешения падение качества реконструкции "ускоряется".
- При удалении гармоник из середины ряда сильный эффект ухудшения качества наблюдается только если затронуты "критичные" гармоники, выялвенные ранее - 10-35.
- При добавлении гармоники выскокого разрешения (т.е. резком увеличении разрешения при уменьшении полноты) качество реконструкции не улучшается.
- Добавление шума к амплитуде сказывается на качестве меньше (чрезвычайно низкое разрешение на 85% зашумления), чем добавление шума к фазе (тот же эффект на 50% зашумления).
- Суммарный эффект шума к амплитуде и к фазе - еще больший, чрезвычайно низкое разрешение уже на 40% шума.
Менее формальные выводы для дальнейших практических импликаций:
- Разрешение модели до 0.85 ангстрем - не дает преимущества, следовательно, к нему не нужно стремиться.
- Разрешение модели 0.85-2.1 можно считать нормальным, т.к. для реконструкции модели белка не нужны точные позиции атомов водорода, да и количество/примерное положение атомов зачастую известны из последовательсти белка.
- Разрешение от 2.14 и до 4.2 можно использовать с опаской, хуже 4.2 не подлежит реконструкции вовсе.
- Полнота ряда - важный фактор, который не должен быть ниже 90%.
- Если полнота ряда низкая, нужно проверить, каких гармоник не хватает. Если нескольких начальных - это не сильно влияет на качество модели. Если каких-то гармоник выше n0 - лучше просто отбросить гармоники высшего порядка, оставить разрешение чуть хуже (профита от добавления гармоник высокого порядка все равно нет никакого)
- Шум в данных - всегда плохо, но зашумление по амплитуде не так страшно, как зашумление по фазе.