Страница седьмого семестра | Учебный сайт Екатерины Швецовой

Реконструкция "одномерного белка" по данным РСА

Создание модельной функции ЭП в одномерной элементарной ячейке

Была создана линейная атомная модель для компьютерного эксперимента: 2 линейных молекулы O-Cl-H и O-C. Для этой модели была смоделирована функция, описывающая одномерную электронную плотность (ЭП) с помощью скрипта compile-func.py:
python compile-func.py -g 8,1.5,8+17,2,9.5+1,1,11+8,1.5,15+6,1.8,16.5

ЭП атомов описываются гауссовской кривой, максимум в центре атома приблизительно пропорционален числу электронов в атоме. Функция задается на интервале [0Å, 30Å]. Гауссова функция определяется числами lambda, beta, gamma по формуле: gauss = lambda*exp(-(beta²)*(X-gamma)²). Lambda - высота гауссовской кривой, соответствующая максимуму электронной плотности в центре атома, пропорциональна числу электронов в атоме, beta - ширина колокола, которая примерно соответствует диаметру атома, gamma - координата максимума гауссовой кривой. Расстояние между молекулами - 4 Å, длина всех связей - 1.5 Å. График электронной плотности модели атомов представлен на рис. 1. Поточечные координаты приведены в файле func.txt.

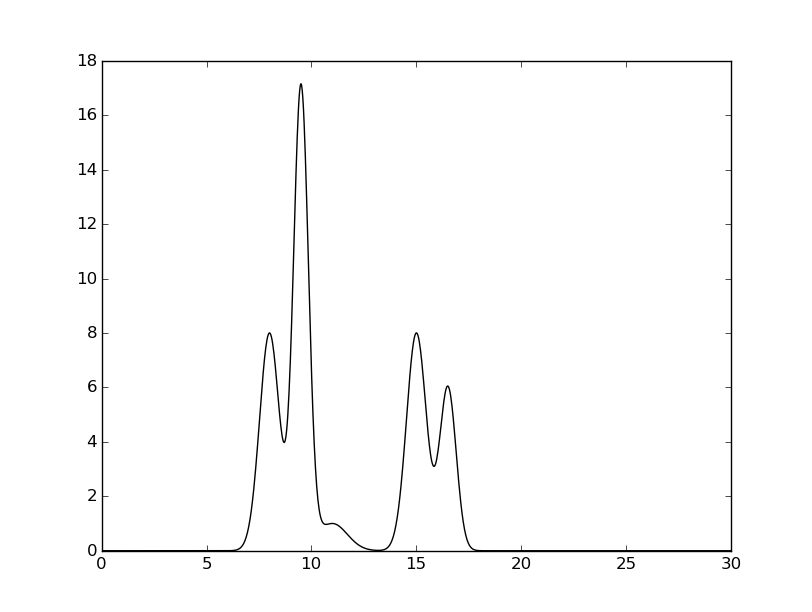
Рис. 1. График электронной плотности 2 линейных молекул O-Cl-H и O-C. По оси абсцисс отложены кординаты атомов в Å, а по оси ординат отложена амплитуда ЭП в условных единицах.

Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные

Амплитуды и фазы рассчитывали по входной функции ЭП. Коэффициенты Фурье рассчитывали с помощью скрипта func2fourier.py. Скрипт по ранее полученному файлу func.txt выдает 499 гармоник на отрезке [0 Å, 30 Å]. Выходной файл скрипта – файл func_ft.txt.

Восстановление функции ЭП по амплитудам и фазам части сигналов

Полные наборы гармоник

По полному набору гармоник был построен график восстановленной функции электронной плотности модели с помощью скрипта fourier2func.py. Этот график полностью совпадает с исходным (см. рис. 2).

Сравнение восстановленной функции ЭП с исходной:

Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
белок является белком дикого типа (структура не содержит экспрессионных тэгов)
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"

Восстановим теперь функцию по меньшему полному набору гармоник. Для отсеивания гармоник использовался скрипт fourier-filter.py. На рис. 2 представлены графики функций, восстановленных по неполному набору гармоник, а именно 0-1, 0-5, 0-10, 0-15, 0-20, 0-25, 0-30.

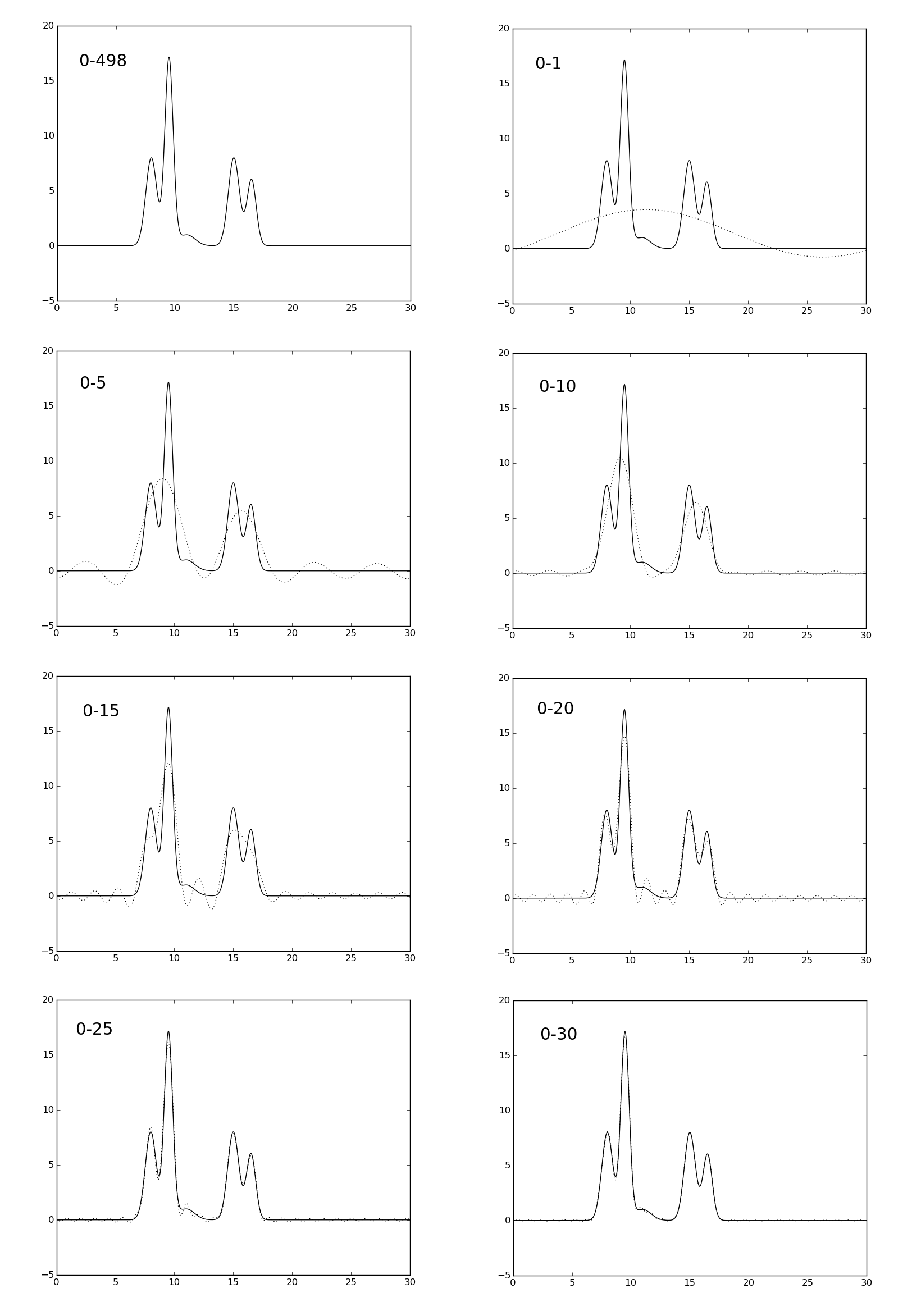
Рис. 2. Графики восстановленных функций ЭП. Графики восстановленных функций, представленны пунктирной линией. Исходная функция представлена в виде сплошной линии.

Анализируя рис. 2 можно придти к выводу, что уже при восстановлении функции по гармоникам 0-25 качетво восстановления отличное (пик, соответствующий водороду можно отличить от шума, он заметно выше). Поэтому будем считать, что 26 - это минимальное число гармоник (n0), при котором функция сохраняет отличное восстановление.

Для добавления шума к амплитудам и/или фазам гармоник использовались опции -F и -P скипта func2fourier.py. Добавление шума приводит к тому, что к каждой амплитуде(F) или фазе (P) прибавляется случайное число, распределенное нормально с а = 0, σ = 0.2*F(или P). Использовались параметры F=10, F=20, P=10, P=20, F=5+P=5, F=10+P=10. Получившиеся изображения восстановленных функций можно увидеть на рис. 3.

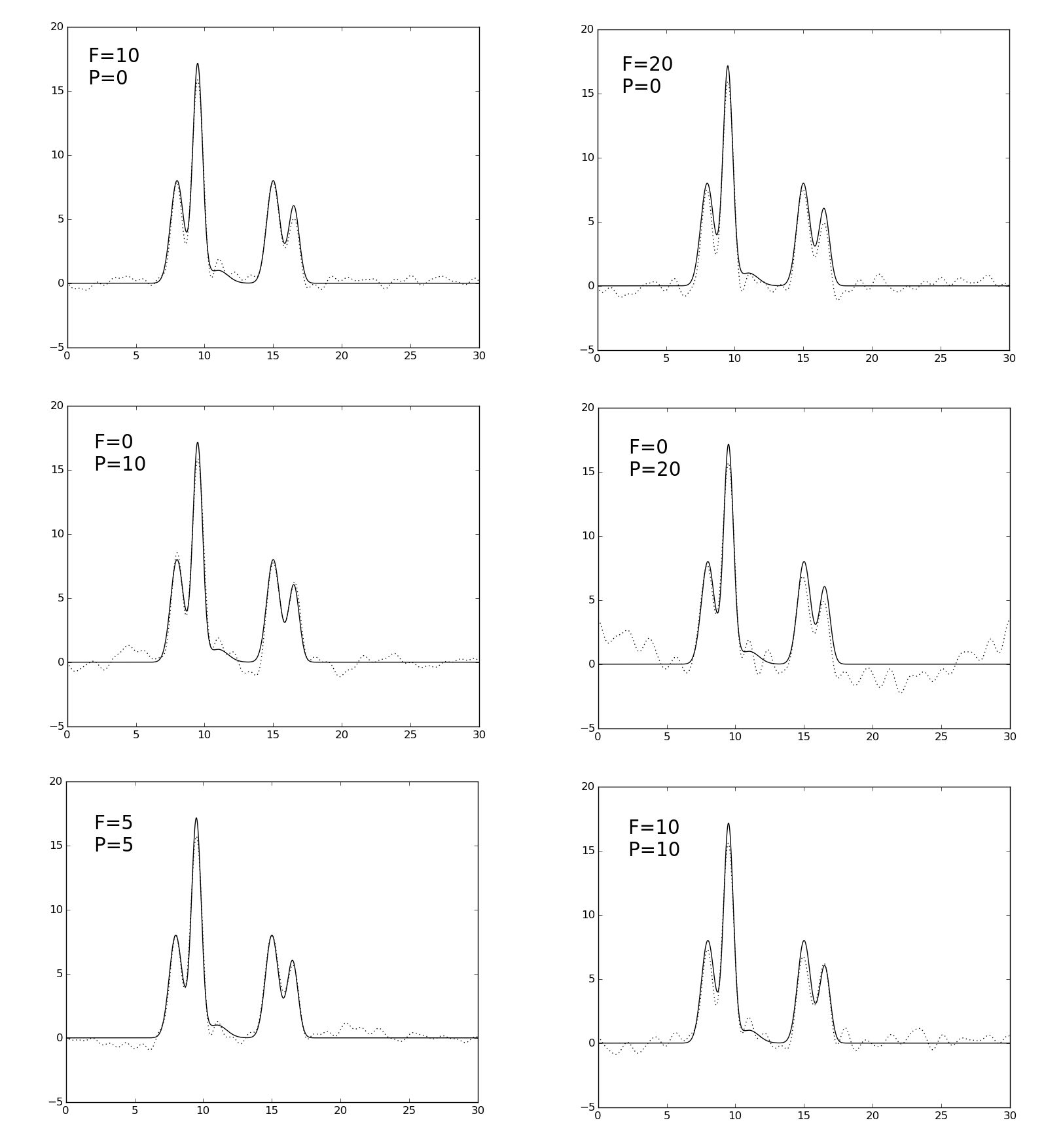
Рис. 3. Графики восстановленных функций с разными уровнями шума (пунктир), наложенные на график исходной функции. Параметры наложенного шума указаны на графиках. Использовался набор гармоник 0-25.

Судя по графикам на рис. 3 можно заключить, что добавление шума к фазе сильнее влияет на качество восстановления, чем добавление шума к амплитуде.

Неполные наборы гармоник Теперь, чтобы сымитировать ситуацию, с которой сталкиваются ученые при расшифровке структур, сделаем неполные наборы гармоник для набора n0: удалим нулевую гармонику, 3 первых гармоники, удалим 2 серединных гармоники, добавим гармонику с номером n0+10 (35). Получившиеся графики можно посмотреть на рис. 4.

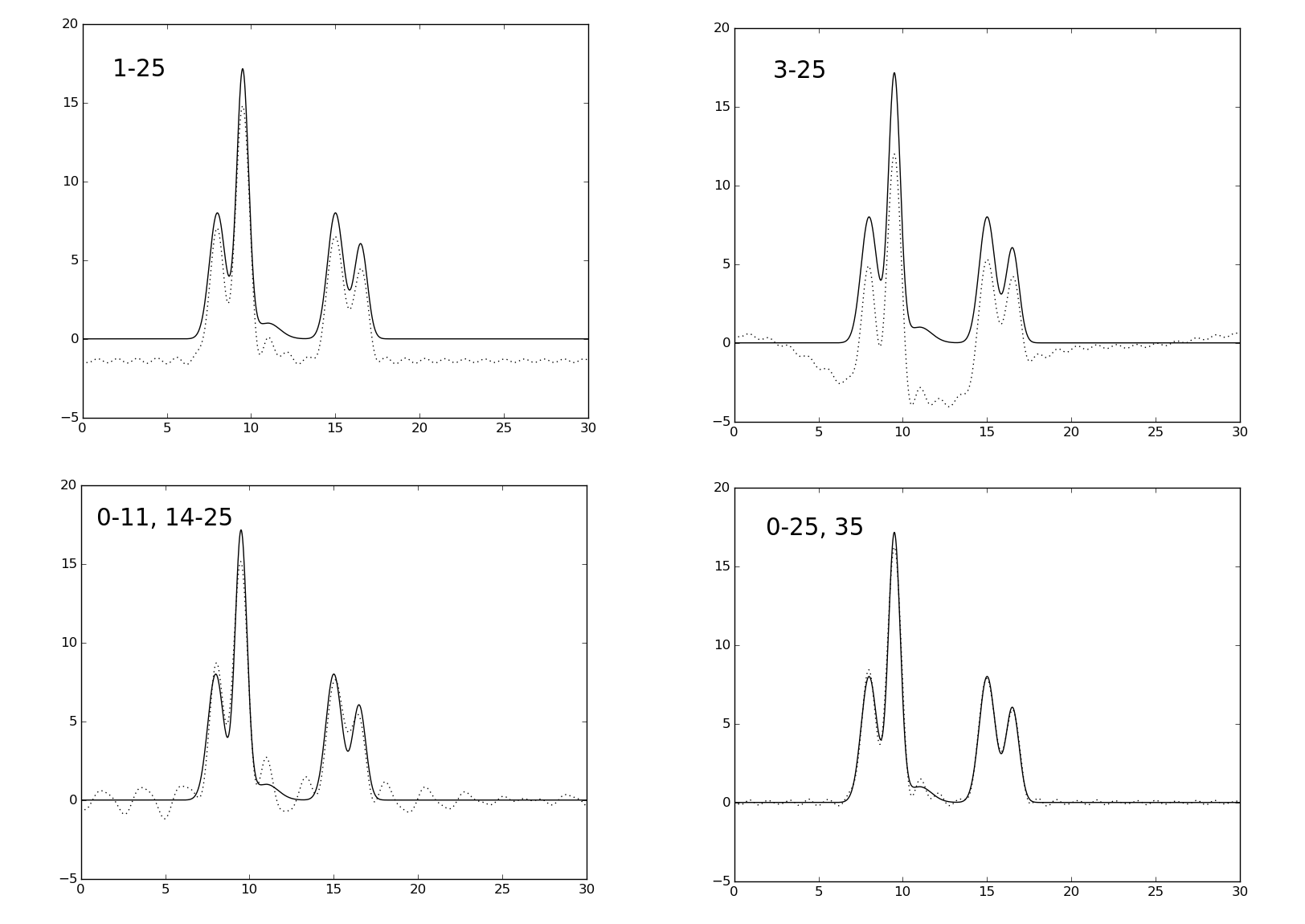
Рис. 4. Графики функций, восстановленных по неполным наборам гармоник. Графики функций, восстановленных по неполному набору гармоник изображены пунктиром, исходная функция - сплошной линией.

При удалении нулевой гармоники функция заметно смещается вниз по оси ординат. Это можно объяснить тем, что эта гармоника есть константа, длины волны у нее нет. Если же удалить первые три, то вычитается синусоида с периодом T/3. Видно, что в этом случае мы наблюдаем "провал" амплитуды для средних значений координат. Вследствие удаления 2 гармоник в середине набора качество восстановления ухудшилось. Добавление гармоники с номером 35 никак не изменило график, т.к. высокочастотные гармоники имеют низкую амплитуду и не могут сильно изменить график.

Итоги

Факторами, влияющими на качество восстановления функции ЭП по гармоникам являются полнота данных и наличие шума. Влияние небольших уровней шума меньше, чем влияние отсутствующих гармоник. Наибольшее влияние шума и неполноты данных оказывается на легкие атомы (атом водорода). Положение более тяжелых атомов определить проще.

Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо сообщить полноту данных — процент гармоник с длиной волны большей d от максимально возможного, присутствующих в наборе. Для полного набора данных (разрешение d=T/n) полнота равна 100%. В качестве примера рассмотрим алгоритм поиска разрешения для неполного набора гармоник (0-25, 35). Если применить разрешение для полного набора, то получится, что разрешение = 0.86, а полнота данных всего 75%. Поэтому разумнее ввести порог на полноту данных 90% и пересчитать разрешение.

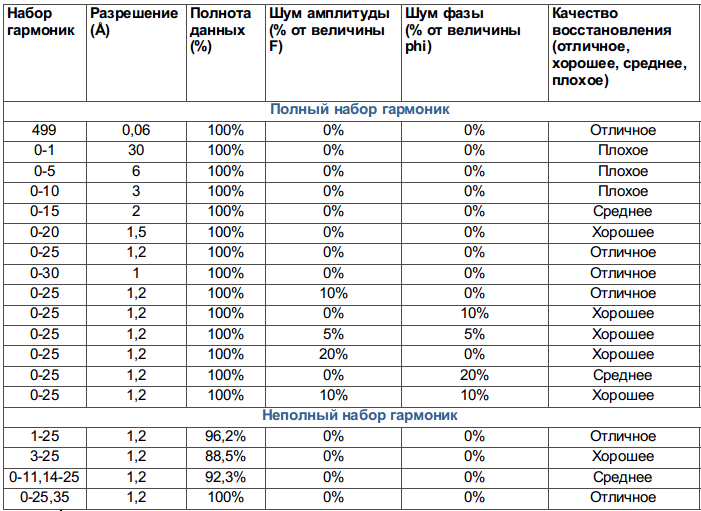
В таблице 1. можно видеть общую информацию о качестве восстановлении функции электронной плотности по всем симуляциям, проведённым в рамках данного пратикума.

Таблица 1. Восстановление функции по коэффициентам ряда Фурье.