Задание функции
Модель: 2 молекулы (5 атомов) расположены на расстоянии около 5 А на отрезке [0, 30]. Электронные плотности описываются гауссовой кривой.Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py
python compile-func.py -g 30,3,3+40,3,4.3+2,3.5,6.5+30,3,7.5
Выходной файл скрипта compile-func.py - текстовый файл func.txt , в котором
описана заданная функция (пары Х-Y). Также с помощью этого скрипта было получено следующее изображение:
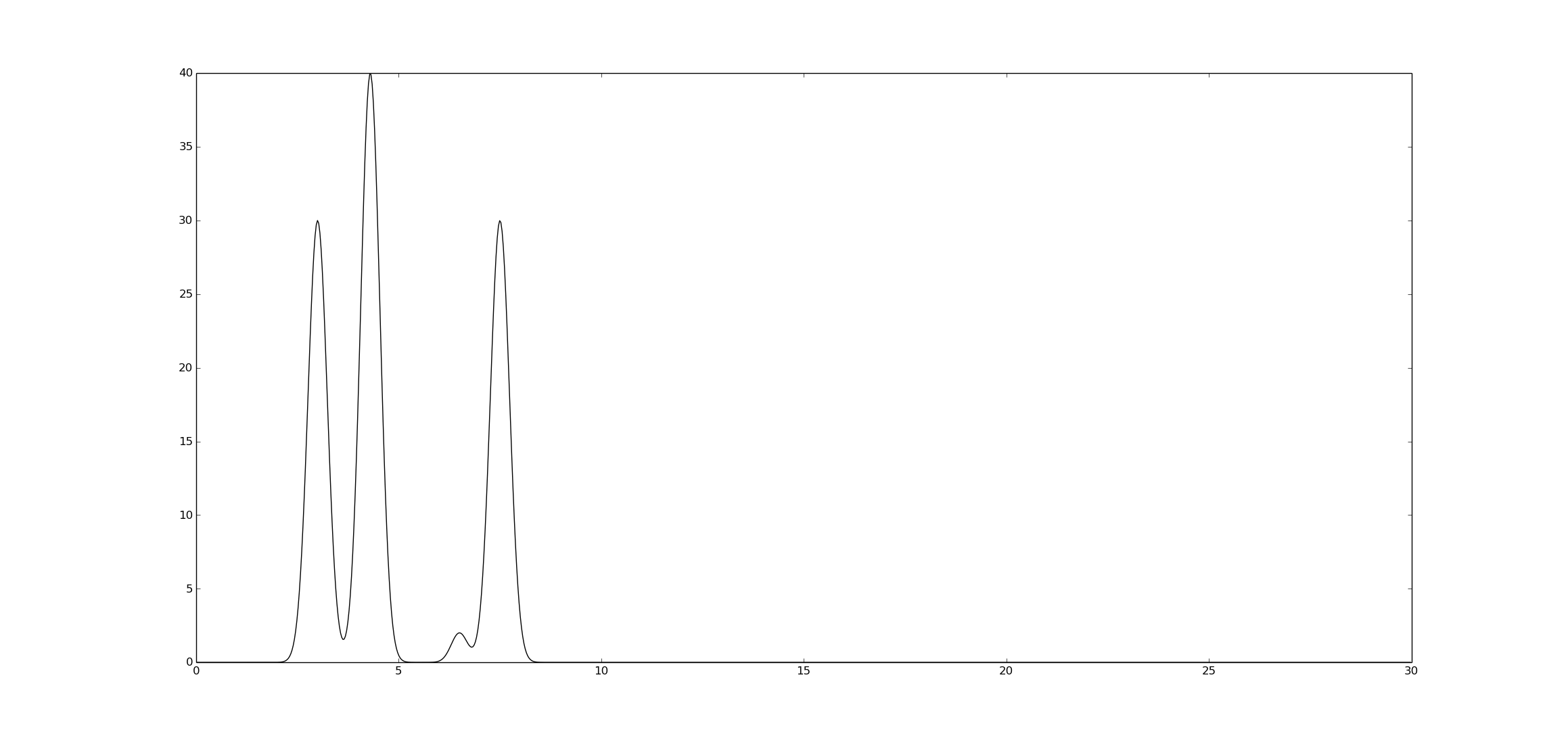
Полные наборы гармоник
Расчет коэффициентов Фурье
Коэффициенты разложения функции в ряд Фурье были получены с помощью скрипта func2fourier.py
python func2fourier.py -i func.txt
Выходной файл скрипта func2fourier.py - текстовый файл func_ft.txt .
В нем приведены амплитуды и фазы гармоник, а также их номера.
Отбор гармоник и восстановление функций Всего 499 гармоник. Надо отобрать их таким образом, чтобы найти n0, для которого по графику восстановленной по полному набору гармоник функции можно было определить положение максимумов всех гауссовых слагаемых.
python fourier-filter.py -r 0-20 -i func_ft.txt -o func_ft_0-20.txt python fourier2func.py -f func.txt -i func_ft_0-20.txt -o two_func_0-20.txt python pourier-filter.py -r 0-30 -i func_ft.txt -o func_ft_0-30.txt python fourier2func.py -f func.txt -i func_ft_0-30.txt -o two_func_0-30.txt python pourier-filter.py -r 0-35 -i func_ft.txt -o func_ft_0-35.txt python fourier2func.py -f func.txt -i func_ft_o-20.txt -o two_func_0-35.txt
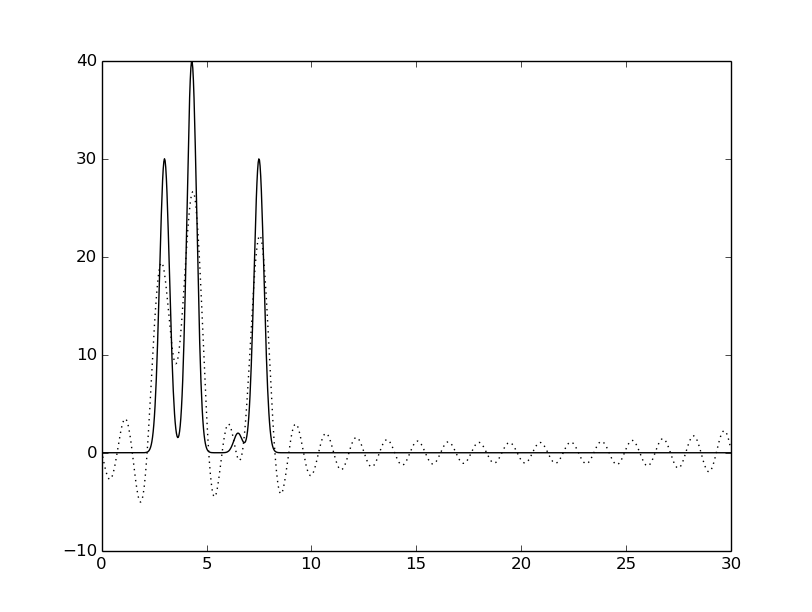
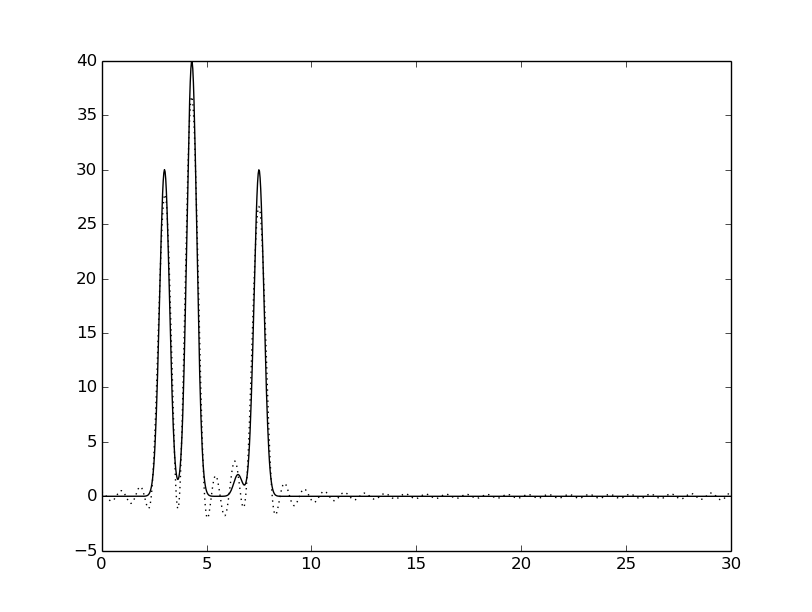
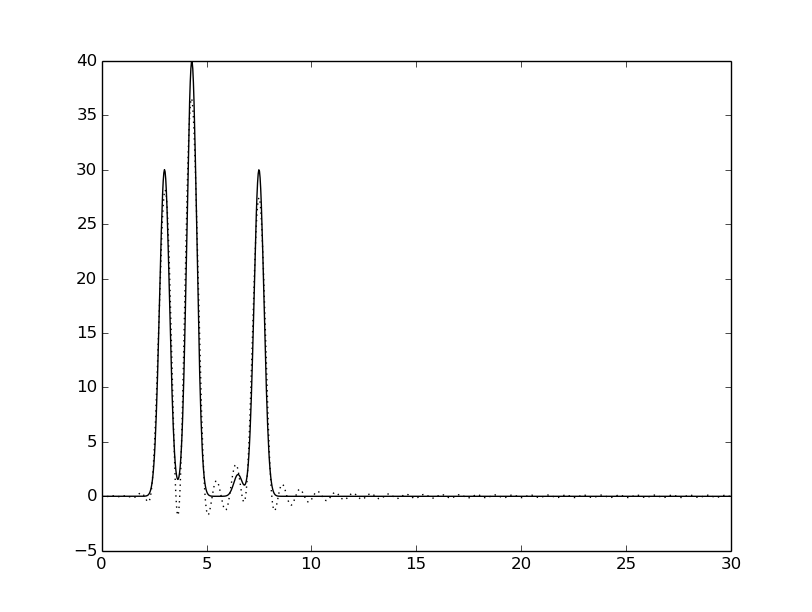
Значение n0 было определено равным 35. Ниже - графики функций для всех n0 (сплошной линией - исходная функция, пунктирной линией - восстановленная функция).
Сравнение восстановленной функции с исходной
Восстановление для n = 20 - среднее, так как не для всех атомов положение максимумов совпадает.
Для n = 30 - хорошее, так как можно угадать положение всех максимумов (зная число слагаемых), но некоторые максимумы плохо отличимы от шума.
Для n = 35 - можно определить положение всех гауссовых слагаемых функции (отличное восстановление).
Попробуем еще бОльшие значения n для полных гармноник:
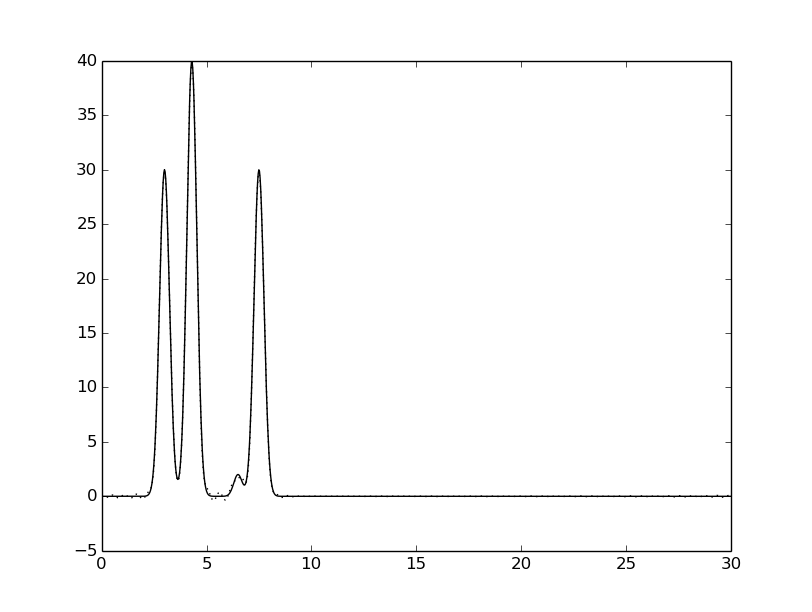
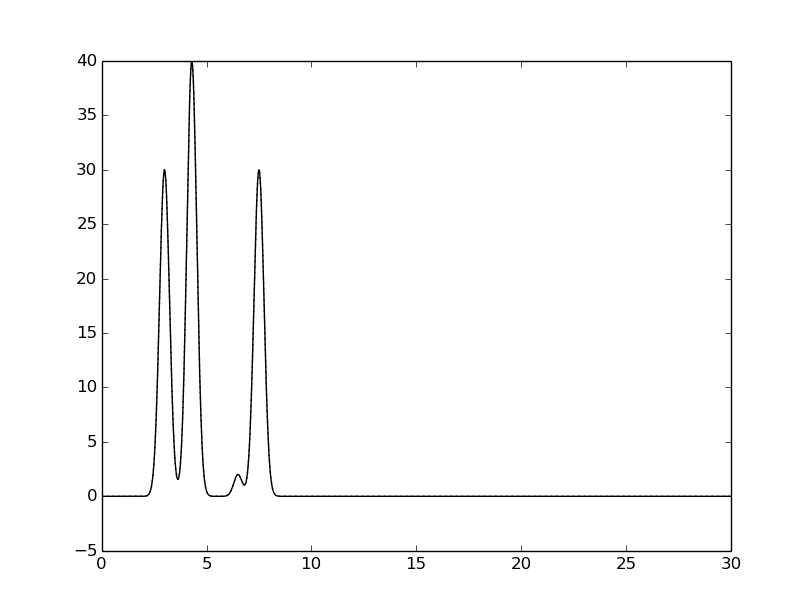
Для n=100 видим полное совпадение восстановленной функции с исходной.
Добавление шума
Команды вида (варьировались значения амплитуды и фазы: -F (0,10,20) и -P (0,10,20)).
python func2fourier.py -F 10 -i func.txt -o ft_nise10-0.txt python furier-filter.py -r 0-35 -i ft_noise10-0.txt -o ft_noise10-0_n0.txt python fourier2func.py -i ft_noise10-0_n0.txt -o two_func_noise10-0_n0.txt
Графики получившихся функций были занесены в таблицу:
 | 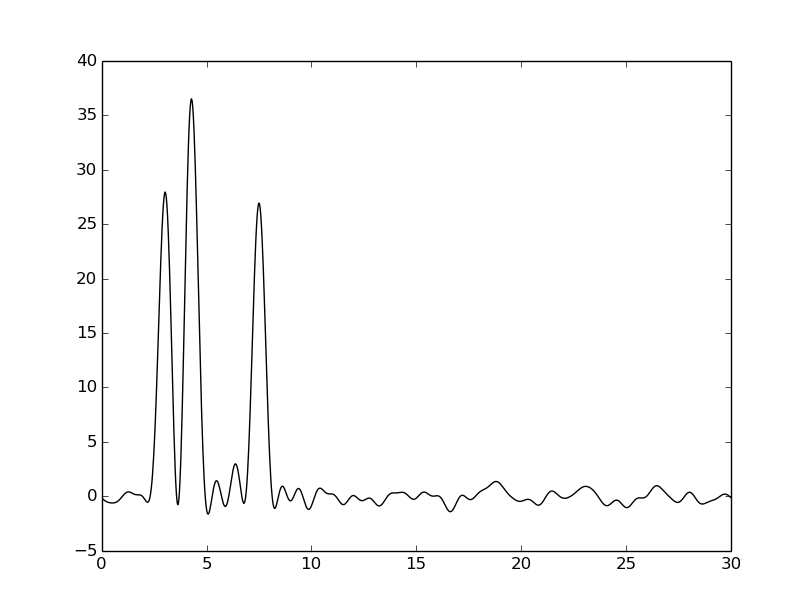 | 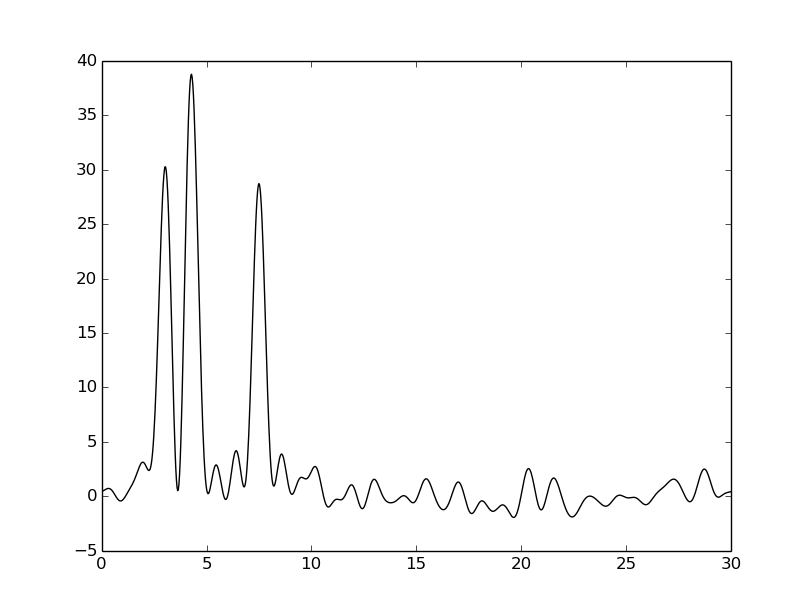 | |
| -P 10 | 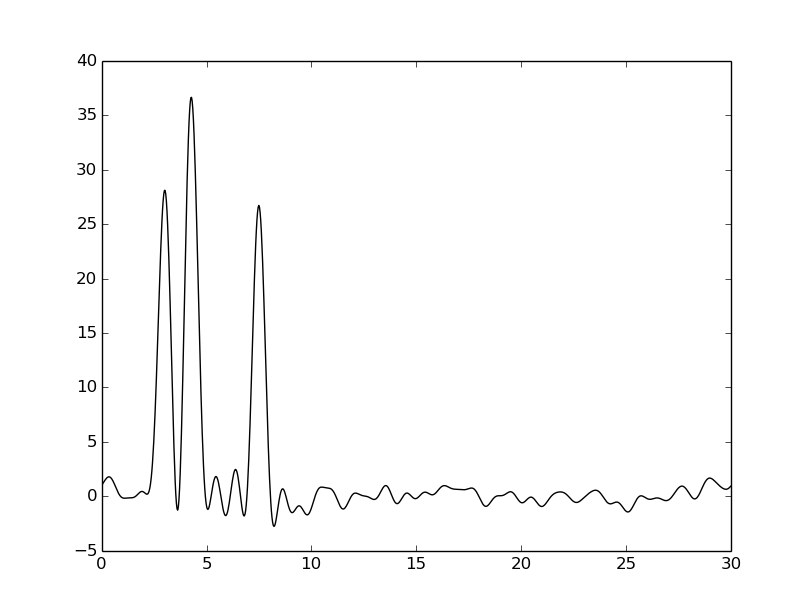 | 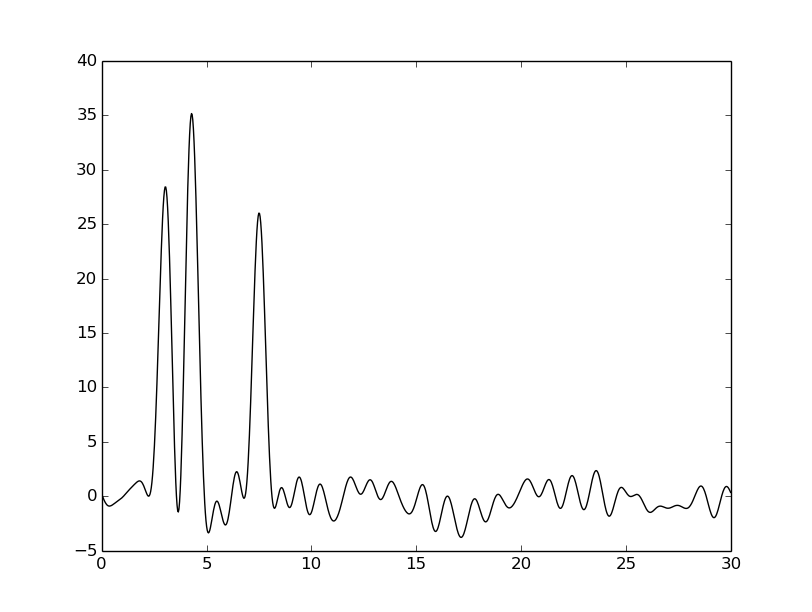 | 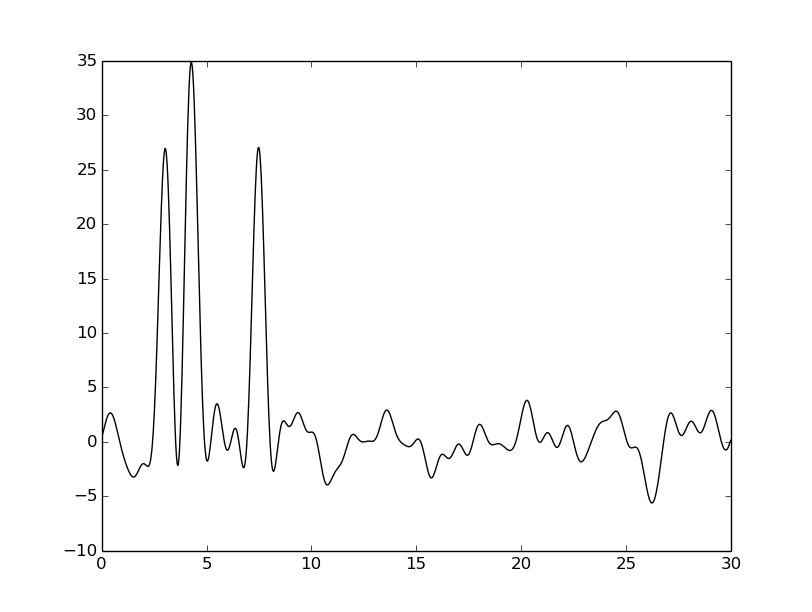 |
| -P 20 | 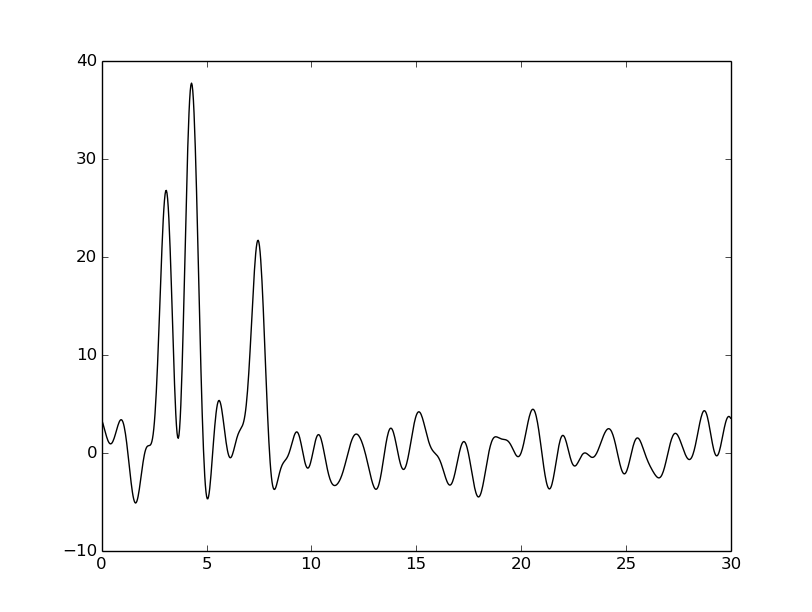 | 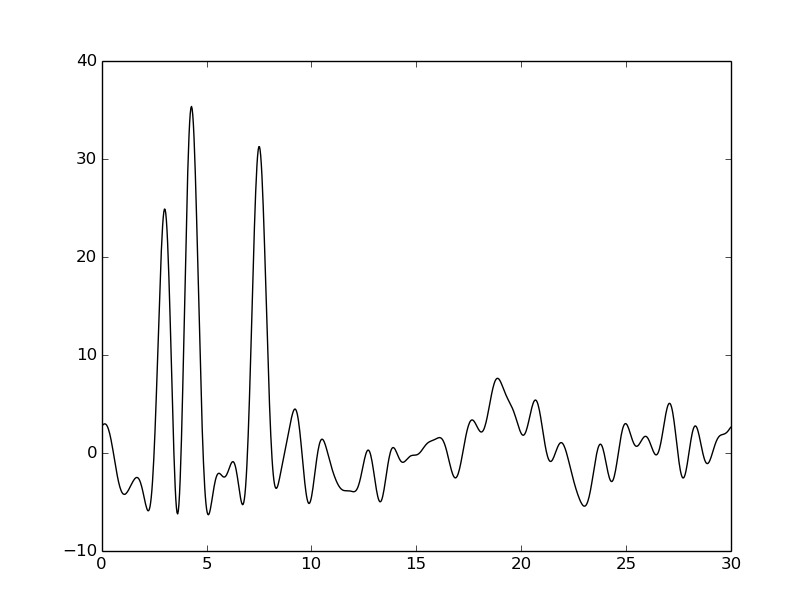 | 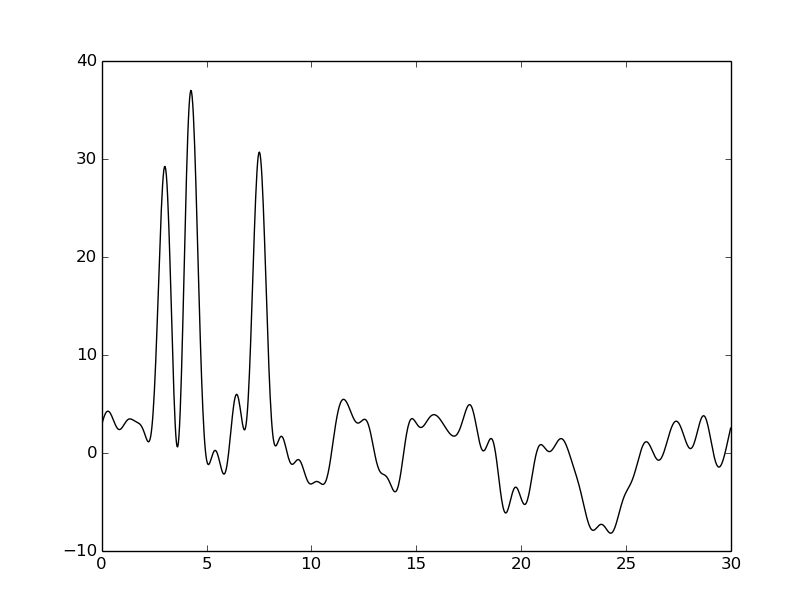 |
Из таблицы видно, что внесение шума к фазе намного сильнее ухудшает восстановление, чем внесение шума к амплитуде. Тем не менее везде видны четыре пика, соответствующие тяжелым атомам, поэтому плохими эти восстановления не назовешь.
Неполные наборы гармоник
Удаление начальных гармоник
Для получения неполного набора гармоник были удалены одна (0) или две (0,1) начальные гармоники.
В случае удаления первой гармоники при восстановлении функции видно, что происходит смещение по оси ординат, однако, на результат
восстановления это никак не влияет (отличное восстановление). Это ожидаемо, так как значение первой гармоники равно числу F0 - первому коэффициенту
ряда Фурье.
В результате удаления первых двух гармоник восстановленная функция заметно искажается, но значения
максимумов остаются на месте (можно однозначно определить).
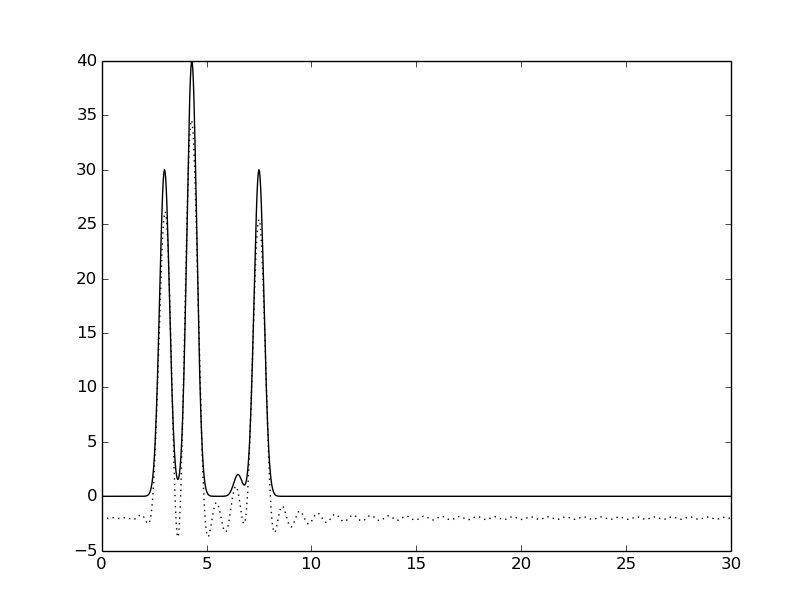
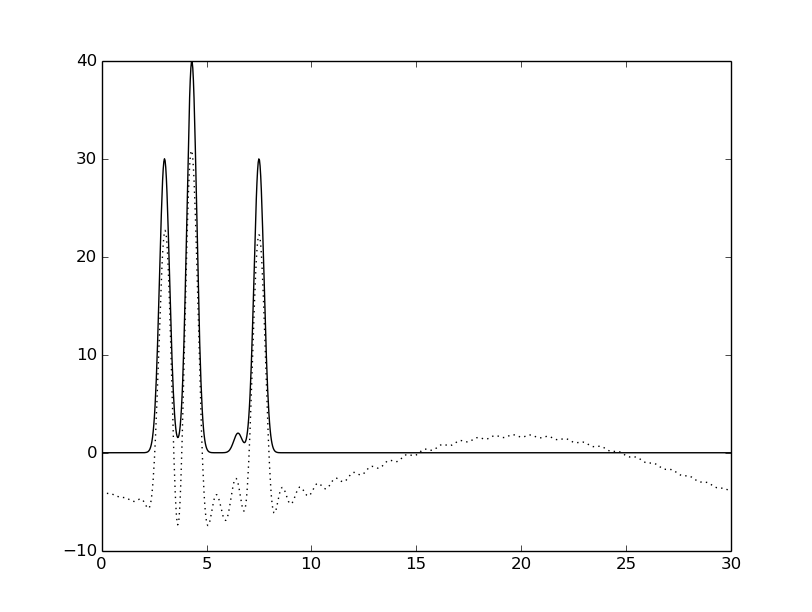
Удаление гармоник из середины набора
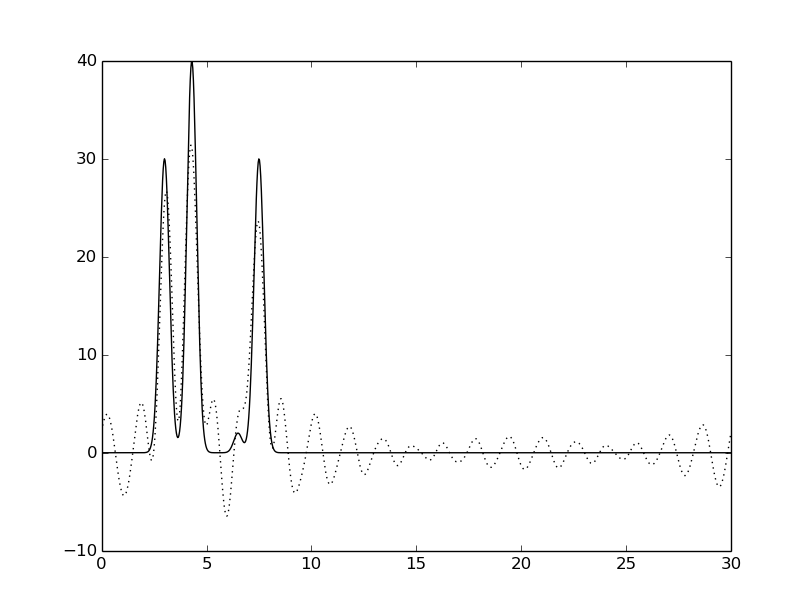
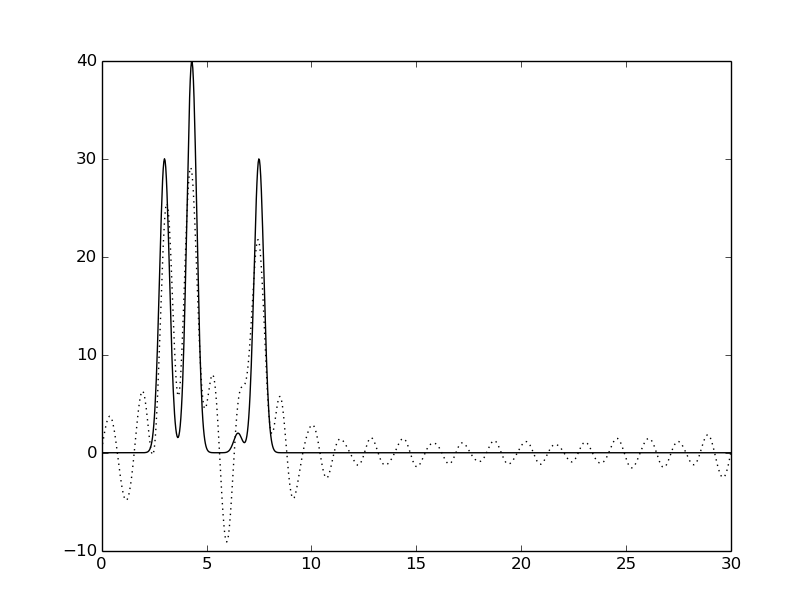
Для получения неполного набора без ~10% гармоник в его середине были удалены гармоники с номерами 17-19 и 16-20.
В обоих случаях удаления (как 14%, так и 8% гармоник) качество восстановления становится значительно хуже (некоторые пики становятся практически неотличимы от шума).
Добавление гармоники n0 + 10
Была добавлена гармоника 45:
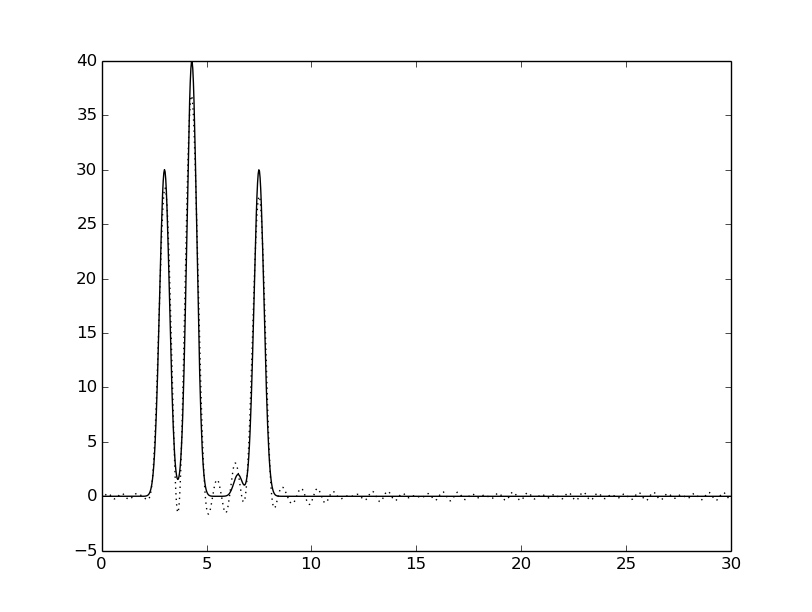
Добавление гармоники 45 не изменило качество восстановления (по сравнению с 0-35 гармониками).
Определение разрешения и полноты данных
Для полного набора гармоник разрешение - период гармоники с наибольшим номером. Для набора гармоника 0-35 разрешение равно 30 А / 35 = 0,86 А.
Полнота данных - как процент гармоник в наборе, период которых не меньше разрешения от числа гармоник в полном наборе для этого разрешения. Для
полного набора полнота данных равна 100%.
Для неполного набора гармоник разумно вводить некоторый порог на полноту данных (например, 85-90%).
| Набор гармоник | Разрешение, Å | Полнота данных, % | Шум амплитуды (% от величины F) | Шум фазы (% от величины P) | Качество восстановления |
| 0-20 | 1.5 | 100 | 0 | 0 | Среднее |
| 0-30 | 1 | 100 | 0 | 0 | Хорошее |
| 0-35 | 0.86 | 100 | 0 | 0 | Отличное |
| 0-35 | 0.86 | 100 | 10 | 0 | Отличное |
| 0-35 | 0.86 | 100 | 0 | 10 | Хорошее |
| 0-35 | 0.86 | 100 | 10 | 10 | Хорошее |
| 0-35 | 0.86 | 100 | 20 | 0 | Хорошее |
| 0-35 | 0.86 | 100 | 0 | 20 | Среднее |
| 0-35 | 0.86 | 100 | 20 | 10 | Хорошее |
| 0-35 | 0.86 | 100 | 10 | 20 | Среднее |
| 0-35 | 0.86 | 100 | 20 | 20 | Среднее |
| 1-35 | 0.86 | 97.2 | 0 | 0 | Отличное |
| 2-35 | 0.86 | 94.4 | 0 | 0 | Отличное |
| 0-16,20-35 | 0.86 | 91.7 | 0 | 0 | Среднее |
| 0-35,40 | 0.86 | 100 | 0 | 0 | Отличное |