1. Зависимость энергии молекулы от длины связи.
Нам дана оптимизированная структура этана в виде z-matrix :
$DATA eth C1 C C 1 cc H 2 ch 1 cchv H 2 ch 1 cch 3 d1 0 H 2 ch 1 cch 3 d2 0 H 1 ch 2 cch 3 d3 0 H 1 ch 2 cch 5 d3 0 H 1 chv 2 cch 4 d3 0 cc=1.52986 ch=1.08439 chv=1.08439 cch=111.200 cchv=111.200 d1=120 d2=-120 d3=180 $END
Необходимо создать 20 разных файлов для расчёта энергии в GAMESS с разными значениями по длине одной из связей (chv). Для этого составляем файл-заготовку для размножения: et.inp . Запускаем GAMESS:
gms et.inp 1 >& et.log
Выходной файл не содержит ошибок. Теперь создаем скрипт, который создает 21 .inp файл с разными значениями для переменной сhv и запускает GAMESS для этих файлов. Полученные .inp и .log файлы можно найти по ссылке . Теперь извлекаем значения энергии из полученных .log файлов. Делаем это с помощью того же скрипта, немного изменив его. Итоговый скрипт: chv.bash . Отправляем полученные значения энергии в файл bond:
bash ./chv.bash > bondС помощью gnuplot можно построить зависимость энергии молекулы от длины одной связи (Рисунок 1):
plot "bond"
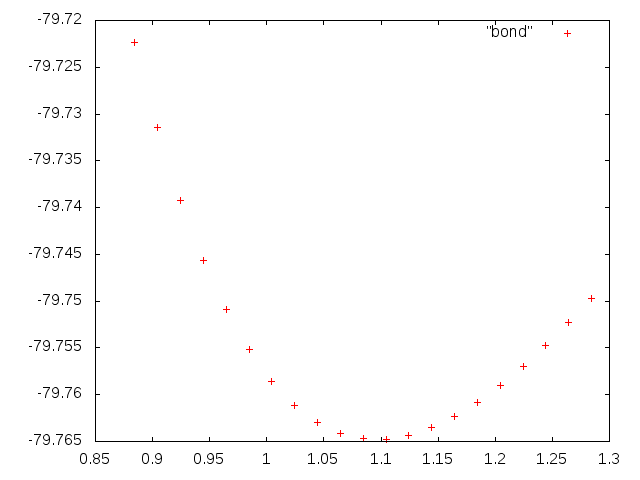
Рисунок 1. Зависимость энергии молекулы от длины одной связи.
Получили график похожий на параболу. Далее будем искать коэффициенты в функции f(x)=a+k(x-b)^2 которые бы позволили наиболее близко описать наблюдаемую зависимость. Для этого воспользуемся возможностями gnuplot. Сначала задаем функцию в развернутом виде, в строке gnuplot вводим: f(x)=a + k*x*x - 2*k*x*b + k*b*b И задаем стартовые значения коэффициентов:
a=-80 k=1 b=1.5
Проводим подгонку коэффициентов под имеющиеся точки в файле bond:
fit f(x) "bond" via a,k,b
Получаем значения коэффициентов:
a = -79.7425+-1.748e+13 k = -0.0212055+-0.01157 b = 1.61439+-6.701e+14
Строим графики функции и значений энергии из GAMESS (рисунок 2):
plot "bond", f(x)
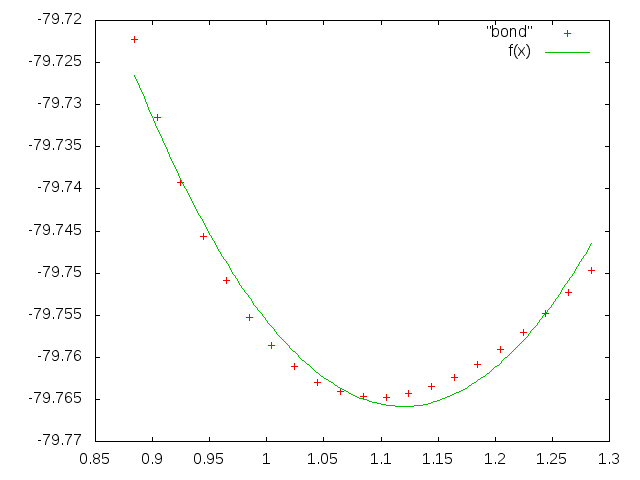
Рисунок 2. Зависимость энергии молекулы от длины одной связи (показана точками) и аппроксимация этой зависимости квадратичной функцией (зеленая кривая).
Полученная кривая не совпадает со значениями энергии. Видимо, зависимость энергии от длины связей надо описывать более сложной функцией.
2. Зависимость энергии молекулы от валентного угла
Выполняем аналогичные действия для валентного угла cchv, меняем угол от 109.2 до 113.2 с шагом 0.2. Полученные в ходе работы файлы .inp и .log можно найти в папке. Итоговый скрипт: cchv.bash. Полученные значения энергии помещены в файл angles:
bash ./cchv.bash > angles
Строим зависимость энергии молекулы от величины одного валентного угла (рисунок 3):
plot "angles"
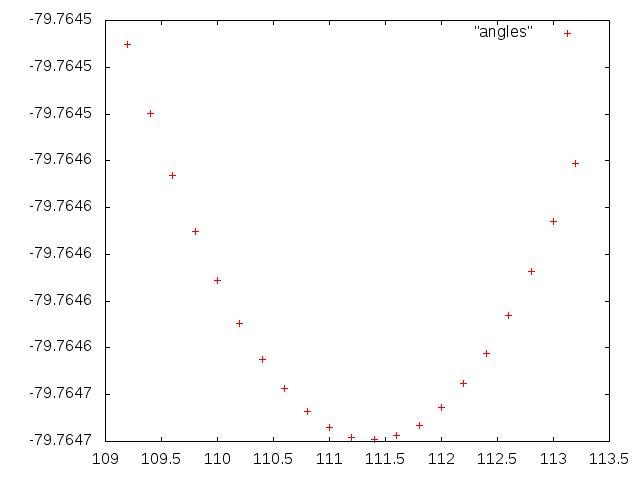
Рисунок 3. Зависимость энергии молекулы величины одного валентного угла.
Полученный график снова аппроксимируем квадратичной функцией. Получили значения коэффициентов:
a=-79.7647 +/-1.21e-08 k=3.56076e-005 +/-6.229e-09 b=111.38 +/-9.954e-05
Строим графики функции и значений энергии из GAMESS (рисунок 4):
plot "angles", f(x)
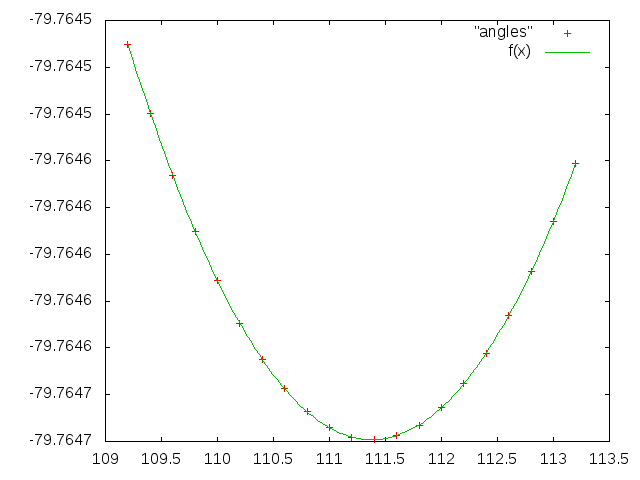
Рисунок 4. Зависимость энергии молекулы от величины одного валентного угла (показана точками) и аппроксимация этой зависимости квадратичной функцией (зеленая кривая).
Полученная кривая очень хорошо совпадает с реальными значениями.
3. Зависимость энергии молекулы от торсионного угла
Выполняем аналогичные действия для торсионного угла d3, меняем угол от -180 до 180 c шагом 12. Полученные в ходе работы файлы .inp и .log можно найти в папке. Итоговый скрипт: d33.bash. Полученные значения энергии помещены в файл torsions:bash ./d3.bash > torsions
Строим зависимость энергии молекулы от величины одного торсионного угла (рисунок 5):
plot "torsions"
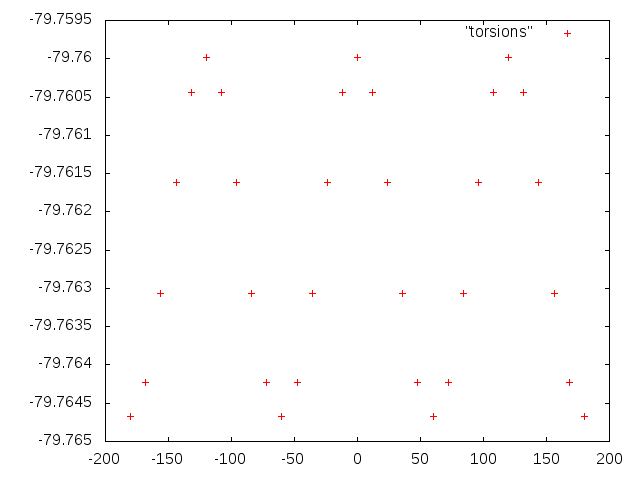
Рисунок 5. Зависимость энергии молекулы величины одного торсионного угла.
Функция имеет три минимума, так как положения, соответствующие значению угла d3 -180 и 180 градусов, не различаются.