Реконструкция ЭП по данным РСА; одномерная модель

Реконструкция ЭП

Для реконструкции ЭП необходимо было создать линейную модель молекул на отрезке [0;30] Å. Я выбрала приблизительную картину для молекулы синильной кислоты и оксида азота II (HCN NO). По характерным длинам связей, радиусам атомов и радиусом Ван-дер-Ваальсовых сфер была написана функция Гаусса, которую принимает на вход скрипт для создания модели (рис. 1). Центры атомов расположены так: H -- 9, C -- 10.6, N -- 11.22, N -- 17, 0 -- 18.25 (Å). Для запуска была использована следующая команда:

python compile-func.py -g 2,2,9+24,3.5,10.06+28,3,11.22+28,3,17+32,3,18.25

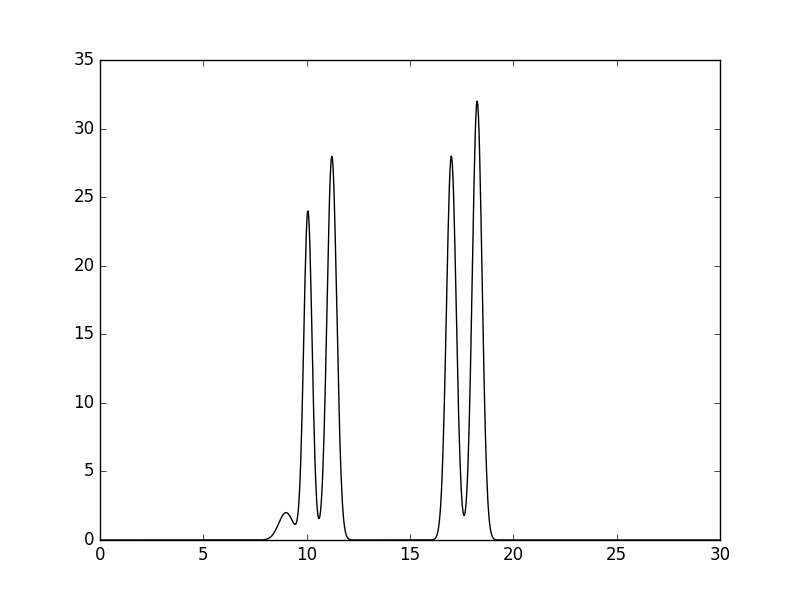
Рис 1. График электронной плотности представленной модели атомов. Поточечные координаты в файле func.txt.

Для разложения функции ЭП в ряд фурье использовался скрипт func2fourier.py, который использует полученный ранее файл func.txt на 499 гармоник и выдает их в файле func_ft.txt.

Полный набор гармоник

По набору гармоник можно восстановить функцию ЭП с помощью скрипта fourier2func.py с разной точностью. Если использовать полный набор гармоник (499), результат будет совпадать с исходным (рис. 2). Если брать лишь часть гармоник, результат будет тем точнее, чем больше их взять (рис. 2). Я отобрала указанные на графиках рис. 2 гармоники для проведения этого эксперимента. Выделить четыре крупных атома удается уже на 19 (0-18) гармониках, хотя определение их центров и ширин пиков будет очень неточным. Чтобы увидеть маленький водород и отличить его от шума надо хотя бы 30 гармоник (на 31 (0-30) уже виден), а лучше взять, например, 36 (0-35). На 0-40 уже все атомы хорошо выделены. Возьмем за достаточный полный набор гармоник для последующих экспериментов 36 первых гармоник.

Рис 2. Восстановление функции ЭП полными наборами гармоник.

Влияние шума

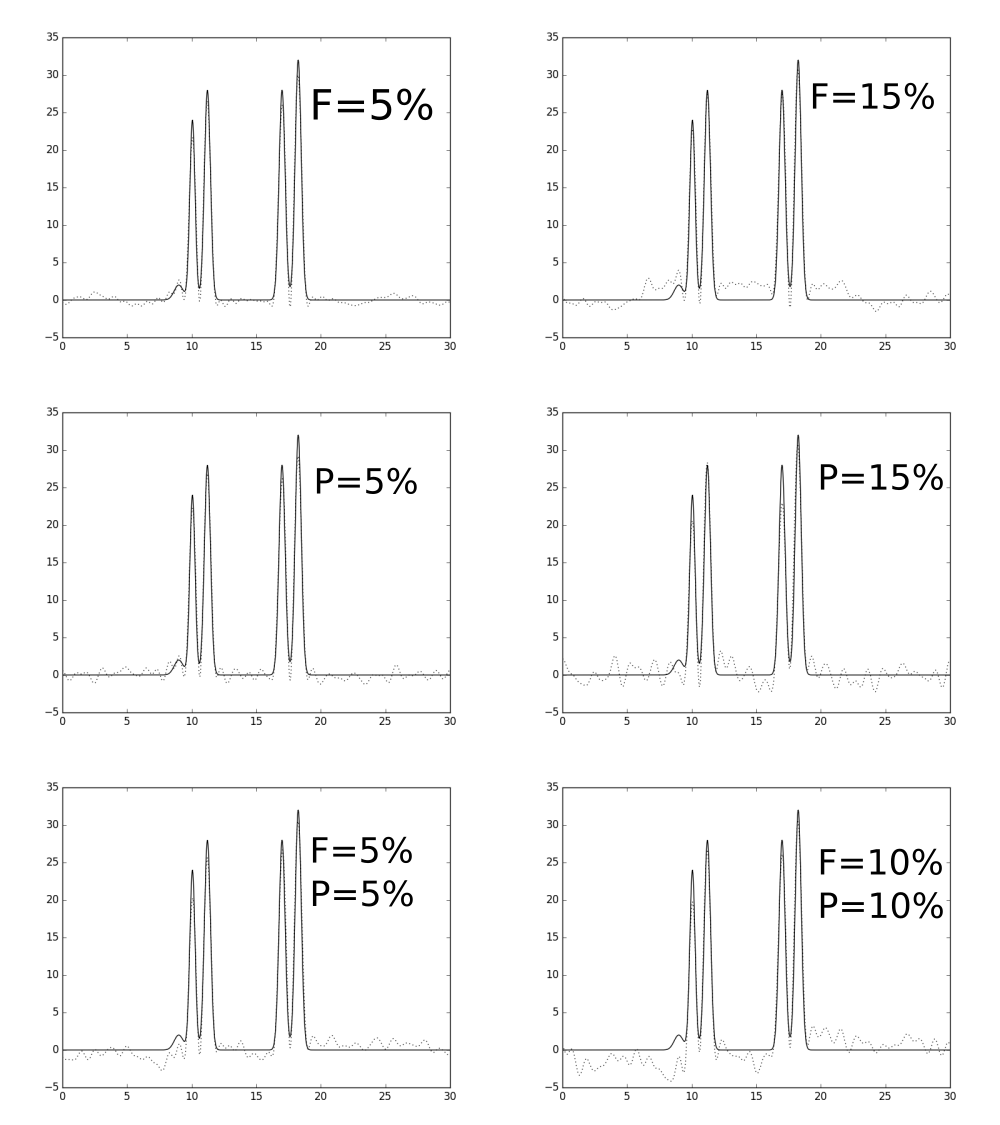
Для изучения влияния шума на восстановление функции ЭП по полному набору гармоник добавим шумы к амплитуде и фазе и попробуем восстановить по 36 гармоникам (рис. 3). Видно, что даже при небольшом шуме различить маленький атом водорода практически не удается, только при 5% по обоим показателям. Заметим, что шум в фазах вносит большее искажение в восстановленную ЭП, чем шум в амплитудах.

Рис 3. Влияние шума на восстановление функции ЭП полным набором из 36 гармоник (0-35).

Неполный набор гармоник

Для изучения восстановления по неполному набору гармоник были взяты следующие варианты: все гармоники пез первой, все гармоники без первых двух, все гармоники без трех в середине, все гармоники и еще одна сильно позже по номеру (рис. 4). Функция ЭП очень хорошо восстанавливается без первой гармоники и без первых двух, но наблюдается сдвиг. А без нескольких гармоник из середины виден существенный шум, водород стал абсолютно таким же, как шум. Добавление "более дальней" гармоники никак не повлияло на восстановление функции ЭП.

Рис 4. Восстановление функции ЭП различными неполными наборами гармоник.

Разрешение

Разрешением полного набора гармоник является период самой высокочастотной гармоники. Для 499 гармоник: d=30Å/499 = 0,06Å, для выбранного нами варианта 36 гармоник: d=30Å/35 = 0,86Å.

Для рассчета разрешения неполного набора гармоник необходимо учитывать еще и полноту данных. Например, в последнем случае с рис. 4, если считать разрешением d=30Å/35 = 0,86Å, полнота будет 100%, а если d=30Å/45 = 0,67Å, то полнота будет уже всего 80%. В случае удаления всего нескольких гармоник из середины (трех) имеет смысл считать разрешением d=30Å/35 = 0,86Å при полноте данных 92%. По соответствующему графику с рис. 4. видно, что уже такая полнота данных добавляет приличный шум, поэтому берут в качестве порога полноты 90-95%. Однако атом водорода в таком случае виден очень плохо, попробуем это учесть (хотя в РСА водороды не определяются) в нашей модели. Тогда d=30Å/15 = 2Å для полноты данных 100%.

Выводы

Таким образом на качество восстановленной функции ЭП влияют количество гармоник и полнота данных и шум. Из шумов больше влияют шумы в фазах. Выбор гармоник влияет больше шума. При равном количестве гармоник лучше качество для набора с большей полнотой, то есть выброшенные из середины гармоники существенно снижают качество. Все результаты собраны в единой таблице.