Восстановление электронной плотности

Задание функции

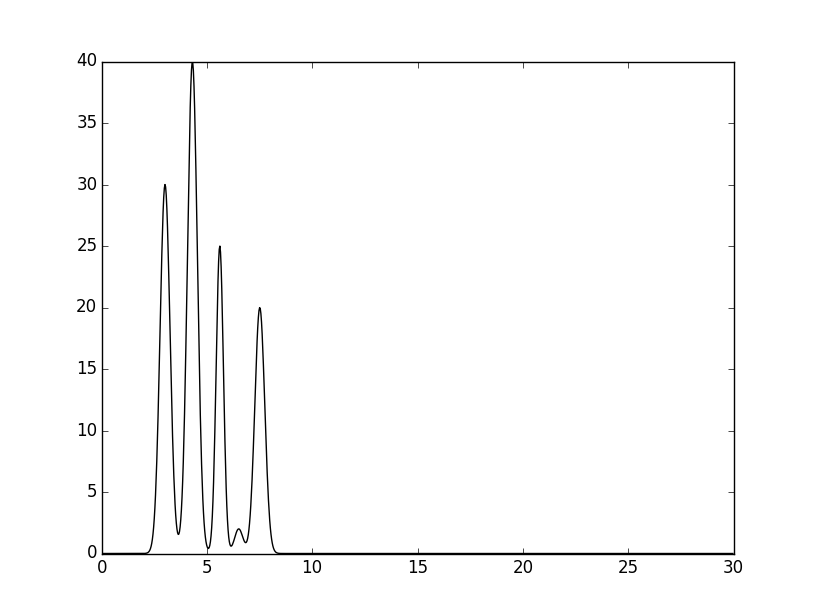
Модель эксперимента: 5 атомов, расположенных на расстоянии ~5 Å на отрезке [0, 30]. Электронные плотности атомов описываются гауссовой кривой. Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py:

Выходной файл скрипта compile-func.py - текстовый файл func.txt, в котором описана заданная функция (в виде пар X – Y). Скрипт также позволяет получить изображение заданной совокупности гауссовых функций (рис. 1).

Рисунок 1.  График заданной функции - совокурность гауссовых функций.

Полные наборы гармоник

Расчёт коэффициентов Фурье

Коэффициенты разложения функции в ряд Фурье были получены с помощью скрипта func2fourier.py:

Выходной файл скрипта func2fourier.py – текстовый файл func_ft.txt. В нём приведены амплитуды и фазы гармоник, а также их номера.

Отбор гармоник и восстановление функций

Из 499 гармоник были отбирались гармоники от 0 до n₀ такие, которых было бы достаточно для восстановления по полному набору гармоник (0, 1, ..., n₀) функции положения максимумов всех гауссовых слагаемых («отличное восстановление»):

Значение n₀ было определено равным 40. Ниже приведены графики (рис. 2-4)восстановленных функций по полным наборам гармоник для n, равных 20, 30 и n₀ = 40 (результат занесен в таблицу 1).

Рисунок 2.  График восстановленной функции, n0 = 20 (сплошная линия - исходная функция, пунктир - восстановленная).	Рисунок 3.  График восстановленной функции, n0 = 30 (сплошная линия - исходная функция, пунктир - восстановленная).	Рисунок 4.  График восстановленной функции, n0 = 40 (сплошная линия - исходная функция, пунктир - восстановленная).

Восстановление для n = 20 можно оценить как «среднее», так как положение не всех атомов можно определить по восстановленной функции. Для n = 30 по восстановленной функции можно угадать положение всех максимумов, но некоторые максимумы плохо отличимы от шума («хорошее восстановление»). При n = 40 уже возможно определить положение всех гауссовых слагаемых функции («отличное восстановление»).

Добавление шума

Затем к амплитудам (F) и фазам (P) был добавлен шум (20% к амплитуде; 20% к фазе; по 10% и 20% к амплитуде и фазе):

Восстановление функции производилось по полному набору гармоник 0, 1, ..., n₀. Качество восстановления заметно снизилось (можно охарактеризовать его как «среднее»), что видно на изображениях (рис. 5-8) и занесено в таблицу 1). Однако везде присутствуют пять пиков, соответствующие тяжелым атомам, поэтому данные восстановления нельзя назвать «плохими».

Рисунок 5.  Добавление шума F = 20 (сплошная линия - исходная функция, пунктир - восстановленная).	Рисунок 6.  Добавление шума P = 20 (сплошная линия - исходная функция, пунктир - восстановленная).
Рисунок 7.  Добавление шума F = 10 и P = 10 (сплошная линия - исходная функция, пунктир - восстановленная).	Рисунок 8.  Добавление шума F = 20 и P = 20 (сплошная линия - исходная функция, пунктир - восстановленная).

Неполные наборы гармоник

Удаление начальных гармоник

Для получения неполного набора гармоник были удалены одна и две начальные гармоники (гармоника с номером 0; гармоники с номерами 0 и 1). В случае удаления первой гармоники (рис. 9) восстановленная функция смещается по оси ординат, однако результат восстановления можно считать «отличным», так как значение первой гармоники равно числу F0 – первому коэффициенту ряда Фурье. В результате удаления первых двух гармоник (рис. 10) восстановленная функция сильно искажается, но значения максимумов четко видны.

Рисунок 9.  График восстановленной функции без первой гармоники (сплошная линия - исходная функция, пунктир - восстановленная).	Рисунок 10.  График восстановленной функции без первой и второй гармоник (сплошная линия - исходная функция, пунктир - восстановленная).

Удаление гармоник из середины набора

Для получения неполного набора гармоник c помощью fourier-filter.py были удалены некоторые гармоники. Удаление как 8% (рис. 11), так и 12% (рис. 12) гармоник в середине набора привело к заметному ухудшению качества восстановления (его можно охарактеризовать как «среднее»). Следовательно, при удалении гармоник в середине набора максимумы от «атомов» становятся менее отличимы от шума.

Рисунок 11.  График восстановленной функции без серединных гармоник 21-23 (сплошная линия - исходная функция, пунктир - восстановленная).	Рисунок 12.  График восстановленной функции без серединных гармоник 11-13, 18-19 (сплошная линия - исходная функция, пунктир - восстановленная).

Добавление гармоники n₀+10

К набору гармоник 0, 1, ..., 40 была добавлена гармоника 50:

Добавление гармоники с номером n₀+10 к набору гармоник 0, 1, ..., n₀ практически не изменило качество восстановления.

Рисунок 13.  График восстановленной функции с гармониками 0-40 и 50 (сплошная линия - исходная функция, пунктир - восстановленная).

Определение разрешения и полноты данных

Для полного набора гармоник разрешение - это период гармоники с наибольшим номером. Для набора гармоник 0-40 разрешение равно 30 Å / 40 ≈ 0,75 Å. Полнота данных определяется как процент гармоник в наборе, период которых не меньше разрешения от числа гармоник в полном наборе для этого разрешения. Для полного набора полнота данных равна 100%.

Таблица 1.  Восстановление функции по коэффициентам ряда Фурье

© Novikova Maria, 2015
Последнее обновление: 25.10.2015