Восстановление электронной плотности

Задание 1. Создание модельной функции электронной плотности в одномерной элементарной ячейке

✧ Модель для компьютерного эксперимента. На отрезке от 0 до 30 (ангстрем) задается функция, имеющая вид нескольких гауссовых кривых. Эти кривые, представляющие собой пики на графике, соответствуюшие электронным плотностям атомов. Максимум электронной плотности в центре атома приблизительно пропорционален числу электронов в атоме. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Всего 6 атомов (3+3). Использовались разные атомы.

✧ Командой

>python compile-func.py -g 5,3.4,4.5+15,3.3,5.6+5,3.2,6.7+5,3.3,10.1+27,3.7,11.4+35,3,12.7

была получена функция с параметрами -g, у которой есть 6 слагаемых, каждое из которых описывает атом. Каждое слагаемое состоит из 3-ех чисел: первое - высота пика (число электронов), второе - ширина пика (размер атома) и третье - положение пика на прямой (1D-пространство, в котором происходит генерация ЭП). Функция показана на рисунке 1, все изображения ниже можно кликнуть и открыть в новом окне в большем масштабе.

Текстовый файл (txt), полученный на выходе работы скрипта compile-func.py (пары X & Y)

Рисунок 1. Функция, имеющая вид нескольких гауссовых кривых, полученная скриптом compile-func.py

Задание 2. Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные

✧ Командой

>python func2fourier.py -i func.txt -o new_function.txt

были получены коэффициенты Фурье. В выходном файле: <номер гармоники (всего их 499)> <амплитуда> <фаза>

Текстовый файл (txt), полученный на выходе работы скрипта func2fourier.py (<номер гармоники> <амплитуда> <фаза>)

Задание 3а. Восстановление функции электронной плотности по модельным ("экспериментальным") данным без шума

✧ Из 499 гармоник, то есть, по полному набору, нужно найти n_0 при котором восстановление отличное.

✧ Командами

>python fourier-filter.py -r 0-5 -i new_function.txt -o function_0_5.txt
>python fourier2func.py -f func.txt -i function_0_5.txt -o function_completed_0_5.txt

получены эти функции, представленные на рисунках 2-7 (сплошной черной линией изображена исходная функция, а пунктиром изображена функция по выбранным гармоникам). Здесь: new_function.txt - файл, полученный на выходе работы скрипта func2fourier.py; func.txt - файл, полученный на выходе работы скрипта compile-func.py (пары X & Y)

Рисунок 2. Гармоники 0-5

Рисунок 3. Гармоники 0-10

Рисунок 4. Гармоники 0-15

Рисунок 5. Гармоники 0-20

Рисунок 6. Гармоники 0-25

Рисунок 7. Гармоники 0-30

✧ n_0 = 30, при котором видны электронные плотности отдельных атомов.

Задание 3б. Восстановление функции электронной плотности по модельным ("экспериментальным") данным с добавлением шума к амплитуде и фазе.

✧ Командами

>python func2fourier.py -F 20 -i func.txt -o function_with_noise_20.txt
>python fourier-filter.py -r 0-30 -i function_with_noise_20.txt -o function_with_noise_20_N0.txt
>python fourier2func.py -i function_with_noise_20_N0.txt .txt -o final_function_with_noise_20_N0.txt

получены эти функции c добавлением шума, представленные на рисунках 8-12 (сплошной черной линией изображена исходная функция, а пунктиром изображена функция с добавлением шума по амплитуде, фазе, или по ним вместе).

Рисунок 8. Гармоники 0-30, добавлен шум 20% к амплитуде

Рисунок 9. Гармоники 0-30, добавлен шум 20% к фазе

Рисунок 10. Гармоники 0-30, добавлен шум 20% к фазе, и к амплитуде

Рисунок 11. Гармоники 0-30, добавлен шум 10% к фазе, и к амплитуде

Рисунок 12. Гармоники 0-30, добавлен шум 15% к фазе, и к амплитуде

Задание 3в. Восстановление функции электронной плотности по модельным ("экспериментальным") данным с использованием неполного набора гармоник. На рисунках ниже сплошной черной линией изображена исходная функция, а пунктиром изображена функция по выбранным гармоникам.

✧ 1) Командами

>python fourier-filter.py -r 1-30 -i new_function.txt -o function_1_30.txt
>python fourier2func.py -f func.txt -i function_1_30.txt -o function_completed_1_30.txt

получена функция, восстановленная по гармоникам 1-30 (то есть, без n=0). Результат на рисунке 13, видно, что график просто сдвинут вниз, так как гармоника n=0 - константа.

Рисунок 13. Гармоники 1-30 (отсутствует гармоника n=0)

✧ 2) На рисунке 14 представлена функция с удаленными из центра гармониками, удалены 10% (3 гармоники - 15,16 и 17)

Рисунок 14. Гармоники 0-14 и 18-30 (отсутствуют гармоники 15-17)

✧ 3) И наконец, на рисунке 15 представлена функция с добавлением гармоники n=40 (0-30,40)

Рисунок 15. Гармоники 0-30 и 40

Вывод

1) Разрешением полного набора гармоник называется период гармоники с номером n, т.е. с наибольшим номером. Период гармоники равен расстоянию между соседними максимумами синусоиды; его также называют длиной волны этой гармоники, хотя никакой физической волны нет. Для полного набора данных (разрешение d=T/n) полнота равна 100%.
2) Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо сообщить полноту данных — процент гармоник с длиной волны больше d от максимально возможного, присутствующих в наборе.

В таблице ниже собрана вся информация по проделанной работе.

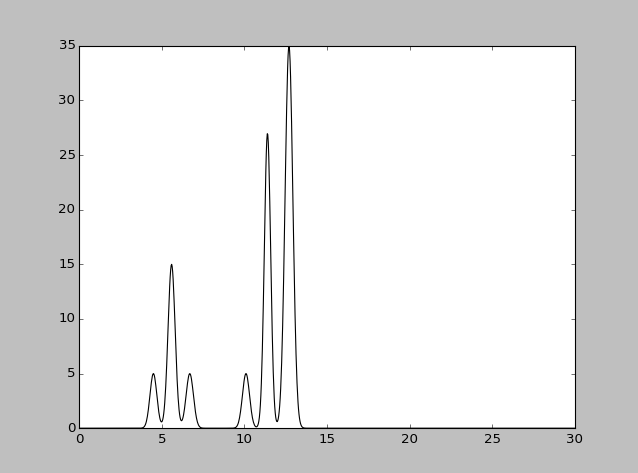
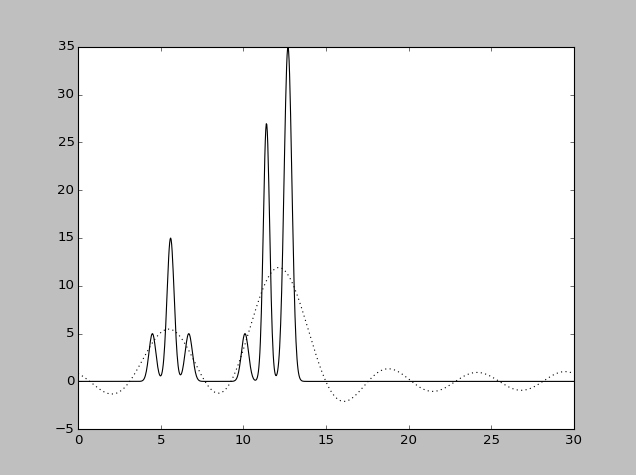
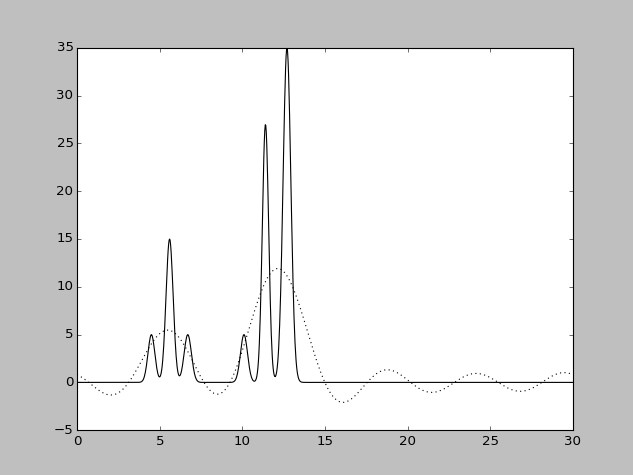
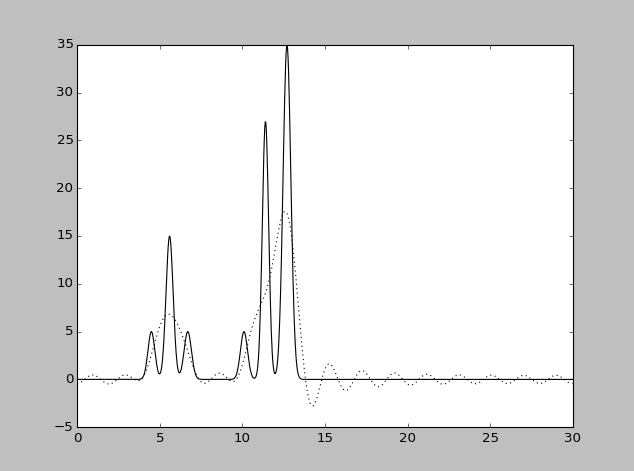
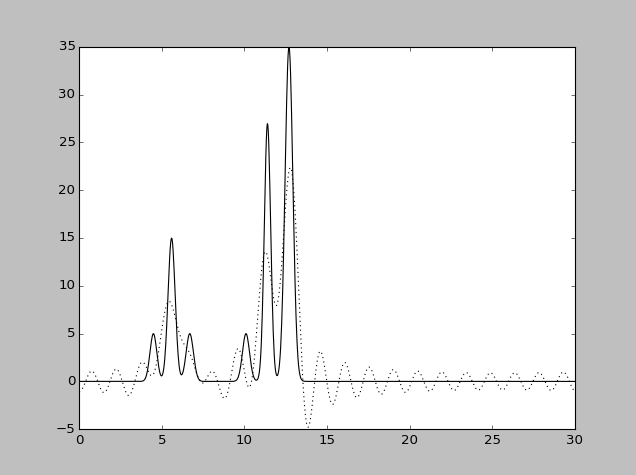
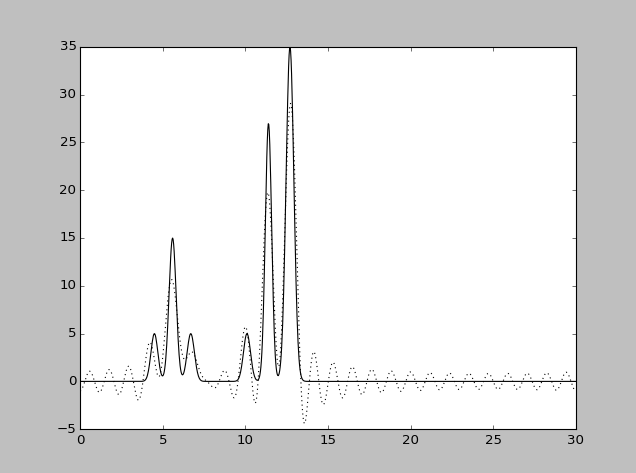
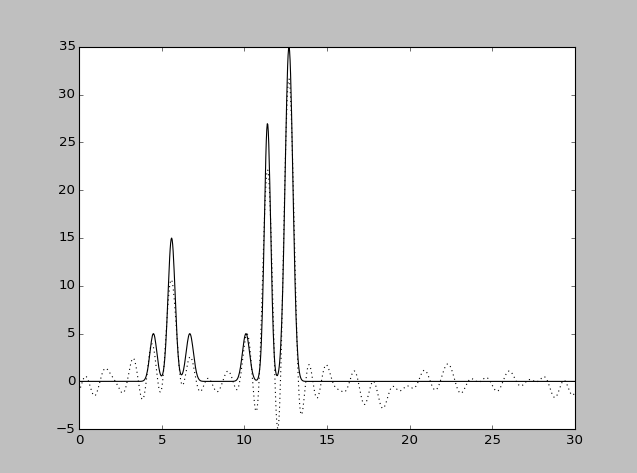
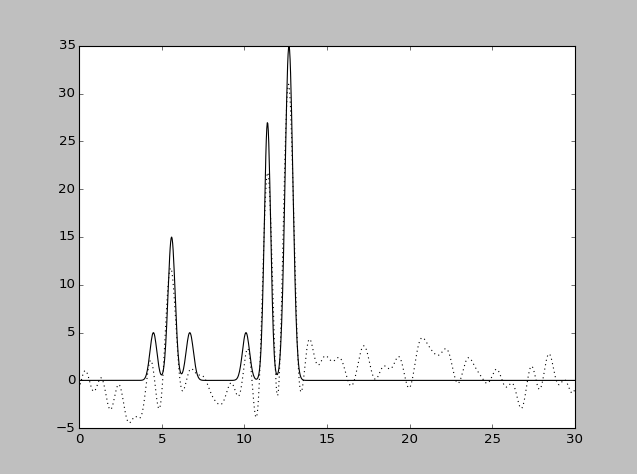
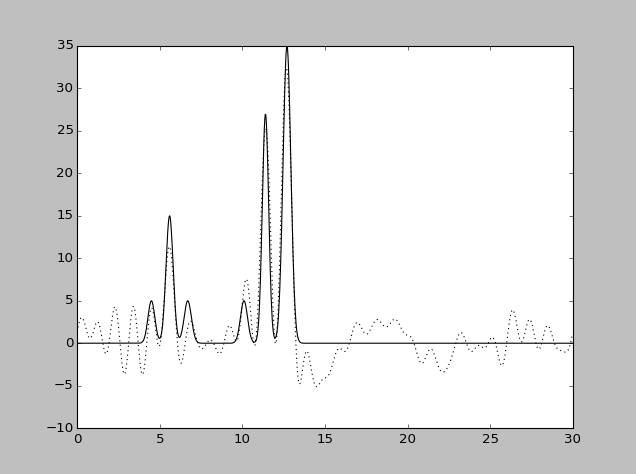
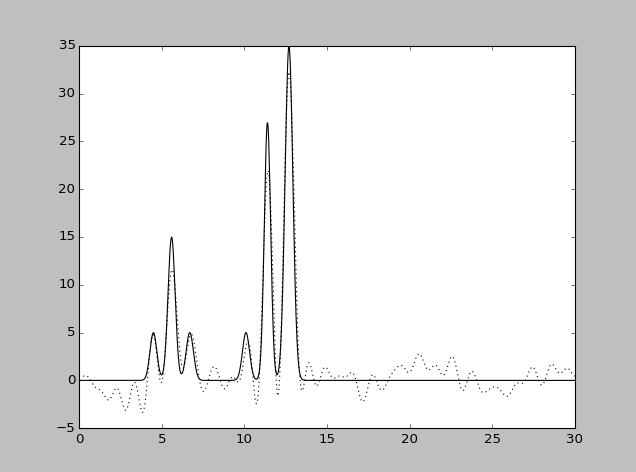
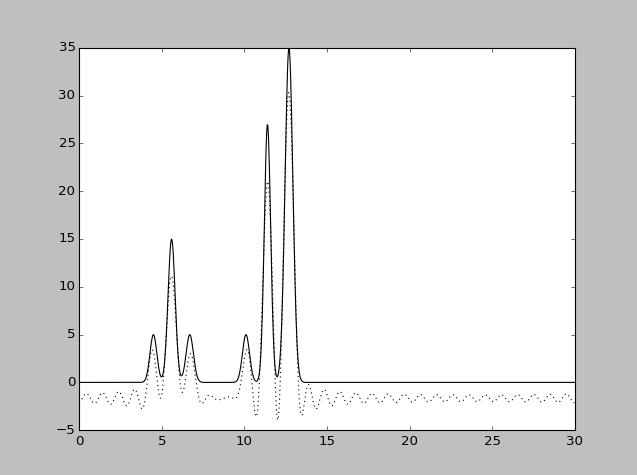
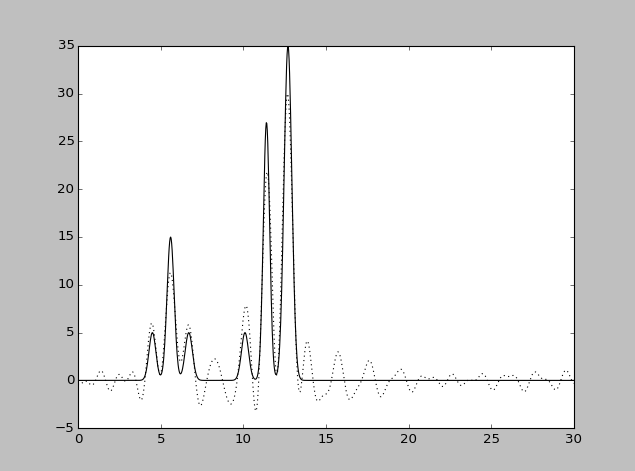
Набор гармоник	Разрешение Å	Полнота данных %	Шум амплитуды (% от величины F)	Шум фазы (% от величины Phase)	Качество восстановления
Полный набор гармоник
0-5	6	100	0	0	Плохое
0-10	3	100	0	0	Плохое
0-15	2	100	0	0	Среднее
0-20	1.5	100	0	0	Среднее
0-25	1.2	100	0	0	Хорошее
0-30	1	100	0	0	Отличное
0-30	1	100	20	0	Хорошее
0-30	1	100	0	20	Среднее
0-30	1	100	20	20	Плохое
0-30	1	100	15	15	Отличное
0-30	1	100	10	10	Отличное
Неполный набор гармоник
1-30	1.1	97	0	0	Отличное
0-14, 18-30	1.25	90	0	0	Хорошее
0-30,40	1	100	0	0	Отличное