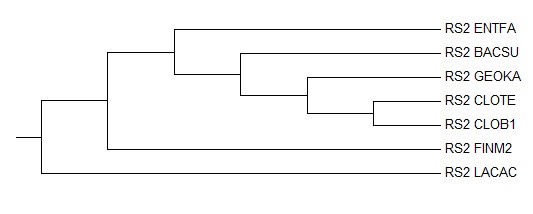
Реконструированное дерево на основе белка RS2
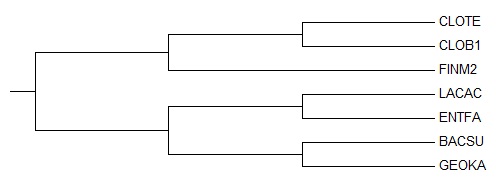
Правильное дерево
Цель занятия: поработать с филогенетическим деревом нескольких бактерий.
На следующих занятиях это дерево будет сравниваться с реконструкциями филогении по последовательностям белков.
Из данного списка бактерий отдела Firmicutes выбираю 7 названий:
| Название | Мнемоника |
| Bacillus subtilis | BACSU |
| Clostridium botulinum | CLOB1 |
| Clostridium tetani | CLOTE |
| Enterococcus faecalis | ENTFA |
| Finegoldia magna | FINM2 |
| Geobacillus kaustophilus | GEOKA |
| Lactobacillus acidophilus | LACAC |
(((CLOTE,CLOB1),FINM2),((LACAC,ENTFA),(BACSU,GEOKA)))

Дерево содержит 4 нетривиальные ветви:
1) {CLOTE, CLOB1} против {FINM2, LACAC, ENTFA, BACSU, GEOKA}
2) {CLOTE, CLOB1, FINM2} против {LACAC, ENTFA, BACSU, GEOKA}
3) {CLOTE, CLOB1, FINM2, BACSU, GEOKA} против {LACAC, ENTFA}
4) {CLOTE, CLOB1, FINM2, LACAC, ENTFA} против {BACSU, GEOKA}
| Название | Таксономическое положение |
| Bacillus subtilis | cellular organisms; Bacteria; Firmicutes; Bacilli; Bacillales; Bacillaceae; Bacillus; Bacillus subtilis group |
| Clostridium botulinum | cellular organisms; Bacteria; Firmicutes; Clostridia; Clostridiales; Clostridiaceae; Clostridium |
| Clostridium tetani | cellular organisms; Bacteria; Firmicutes; Clostridia; Clostridiales; Clostridiaceae; Clostridium |
| Enterococcus faecalis | cellular organisms; Bacteria; Firmicutes; Bacilli; Lactobacillales; Enterococcaceae; Enterococcus |
| Finegoldia magna | cellular organisms; Bacteria; Firmicutes; Clostridia; Clostridiales; Clostridiales incertae sedis; Clostridiales Family XI. Incertae Sedis; Finegoldia |
| Geobacillus kaustophilus | cellular organisms; Bacteria; Firmicutes; Bacilli; Bacillales; Bacillaceae; Geobacillus |
| Lactobacillus acidophilus | cellular organisms; Bacteria; Firmicutes; Bacilli; Lactobacillales; Lactobacillaceae; Lactobacillus |
На дереве отобранных бактерий есть ветви, выделяющие таксоны:
1) Ветвь {CLOTE, CLOB1} выделяет Clostridium от остальных.
2) Ветвь {CLOTE, CLOB1, FINM2} выделяет Clostridiales от Bacilli.
3) Ветвь {LACAC, ENTFA} выделяет Lactobacillales от остальных.
4) Ветвь {BACSU, GEOKA} выделяет Bacillaceae от остальных.
Таким образом, легко заметить, что разделение на ветви соответствует таксономическому положению бактерий.
Из данного списка функций белков выбираю одну: Рибосомный белок S2 (RS2). По белкам соответствующего семейства
будем реконструировать филогенетическое дерево.
Для получения выравнивания использую команду muscle -in data.fasta -out datav.fasta.
Вводим команду: fprotpars datav.fasta -outtreefile data.treefile -outfile data.fprotpars.
В результате программа выдала только один вариант дерева: (((RS2_ENTFA,(RS2_BACSU,(RS2_GEOKA,(RS2_CLOTE,RS2_CLOB1)))),RS2_FINM2),RS2_LACAC)
Реконструированное дерево на основе белка RS2 |
Правильное дерево |
Вводим команду: fprotdist datav.fasta -outfile data.fprotdist.
7
RS2_LACAC 0.000000 0.532973 0.473286 0.485131 0.446305 0.468935 0.480286
RS2_FINM2 0.532973 0.000000 0.382930 0.387458 0.551788 0.481519 0.402736
RS2_CLOB1 0.473286 0.382930 0.000000 0.134211 0.389508 0.371016 0.374811
RS2_CLOTE 0.485131 0.387458 0.134211 0.000000 0.413648 0.384315 0.340334
RS2_ENTFA 0.446305 0.551788 0.389508 0.413648 0.000000 0.332305 0.336838
RS2_BACSU 0.468935 0.481519 0.371016 0.384315 0.332305 0.000000 0.122655
RS2_GEOKA 0.480286 0.402736 0.374811 0.340334 0.336838 0.122655 0.000000
Ультраметричность: Рассмотрим тройку {RS2 GEOKA, RS2 CLOTE, RS2 CLOB1}. Видим следующее: если d(GEOKA,CLOB1)=0.374811 > d(CLOB1,CLOTE)=0.134211
(что выполняется), то d(GEOKA,CLOB1)=0.374811 = d(GEOKA,CLOTE)=0.340334 (что не выполняется). Тем не менее расстояния отклоняются от
ультраметричности не на много.
Аддитивность: Рассмотрим четверку {RS2 ENTFA, RS2 GEOKA, RS2 BACSU, RS2_LACAC}. Видим следующее: d(ENTFA,GEOKA)+d(BACSU,LACAC)=0.336838+0.468935=0,805773,
d(ENTFA,LACAC)+d(GEOKA,BACSU)=0.446305+0.122655=0,56896, d(ENTFA,BACSU)+d(GEOKA,LACAC)=0,332305+0.480286=0,812591. Получилось, что две
суммы почти равны между собой и больше третьей, что говорит о выполнении свойства аддитивности.
Neighbor-Joining:
+-------------RS2_FINM2
+--3
! ! +---RS2_CLOB1
! +----2
! +---RS2_CLOTE
!
! +----------RS2_ENTFA
4-5
! ! +---RS2_BACSU
! +-----1
! +--RS2_GEOKA
!
+---------------RS2_LACAC
Неукорененное дерево!
Between And Length
------- --- ------
4 3 0.05061
3 RS2_FINM2 0.23901
3 2 0.07908
2 RS2_CLOB1 0.06337
2 RS2_CLOTE 0.07085
4 5 0.03029
5 RS2_ENTFA 0.17816
5 1 0.09508
1 RS2_BACSU 0.07164
1 RS2_GEOKA 0.05102
4 RS2_LACAC 0.26289
|
UPGMA:
+-------------RS2_LACAC
!
--6 +------------RS2_FINM2
! !
+-5 +---RS2_CLOB1
! +------2
! ! +---RS2_CLOTE
+-4
! +---------RS2_ENTFA
+-3
! +--RS2_BACSU
+------1
+--RS2_GEOKA
From To Length Height
---- -- ------ ------
6 RS2_LACAC 0.24058 0.24058
6 5 0.01993 0.01993
5 RS2_FINM2 0.22064 0.24058
5 4 0.03117 0.05111
4 2 0.12236 0.17347
2 RS2_CLOB1 0.06711 0.24058
2 RS2_CLOTE 0.06711 0.24058
4 3 0.02218 0.07329
3 RS2_ENTFA 0.16729 0.24058
3 1 0.10596 0.17925
1 RS2_BACSU 0.06133 0.24058
1 RS2_GEOKA 0.06133 0.24058
|
Сравниваем эти две реконструкции между собой:
1) Первая реконструкция представляет собой неукорененное дерево в отличие от второй.
2) Нетривиальные ветви:
Neighbor-Joining:
1. {RS2_CLOB1, RS2_CLOTE} против {RS2_FINM2, RS2_ENTFA, RS2_BACSU, RS2_GEOKA, RS2_LACAC}
2. {RS2_CLOB1, RS2_CLOTE, RS2_FINM2} против {RS2_ENTFA, RS2_BACSU, RS2_GEOKA, RS2_LACAC}
3. {RS2_BACSU, RS2_GEOKA} против {RS2_CLOB1, RS2_CLOTE, RS2_FINM2, RS2_ENTFA, RS2_LACAC}
4. {RS2_BACSU, RS2_GEOKA, RS2_ENTFA} против {RS2_CLOB1, RS2_CLOTE, RS2_FINM2, RS2_LACAC}
UPGMA:
1. {RS2_CLOB1, RS2_CLOTE} против {RS2_FINM2, RS2_ENTFA, RS2_BACSU, RS2_GEOKA, RS2_LACAC}
2. {RS2_BACSU, RS2_GEOKA} против {RS2_CLOB1, RS2_CLOTE, RS2_FINM2, RS2_ENTFA, RS2_LACAC}
3. {RS2_BACSU, RS2_GEOKA, RS2_ENTFA} против {RS2_CLOB1, RS2_CLOTE, RS2_FINM2, RS2_LACAC}
4. {RS2_CLOB1, RS2_CLOTE, RS2_FINM2} против {RS2_ENTFA, RS2_BACSU, RS2_GEOKA, RS2_LACAC}
Таким образом, оба дерева имеют одни и теже ветви. С правильным деревом сходятся только 3 из 4-х.
Если сравнивать эти две реконструкции с деревом, полученным программой fprotpars, то реконструкции Neighbor-Joining и UPGMA
являются более достоверными. Как уже отмечалось выше, дерево по fprotpars имеет только 1 общую ветвь с верным.
Теперь рассмотрим оценки расстояний:
Neighbor-Joining:
Ультраметричность: {RS2 GEOKA, RS2 CLOTE, RS2 CLOB1}:
Видим следующее: если d(GEOKA,CLOB1)=0.36945 > d(CLOB1,CLOTE)=0.13422 (что выполняется),
то d(GEOKA,CLOB1)=0.36945 = d(GEOKA,CLOTE)=0.376993 (что можно сказать тоже выполняется).
Таким образом, свойство ультраметричности выполняется.
Аддитивность:
{RS2 ENTFA, RS2 GEOKA, RS2 BACSU, RS2_LACAC}:
Видим следующее: d(ENTFA,GEOKA)+d(BACSU,LACAC)=0.32426+0.4599=0,78416,
d(ENTFA,LACAC)+d(GEOKA,BACSU)=0.47134+0.12266=0,594, d(ENTFA,BACSU)+d(GEOKA,LACAC)=0,34488+0.43928=0,78416.
Получилось, что две суммы абсолютно равны между собой и больше третьей, что говорит о выполнении свойства аддитивности.
UPGMA:
Ультраметричность: {RS2 GEOKA, RS2 CLOTE, RS2 CLOB1}:
Видим следующее: если d(GEOKA,CLOB1)=0.37894 > d(CLOB1,CLOTE)=0.13422 (что выполняется),
то d(GEOKA,CLOB1)=0.37894 = d(GEOKA,CLOTE)=0.37894 (что тоже выполняется).
Таким образом, свойство ультраметричности выполняется.
Аддитивность:
{RS2 ENTFA, RS2 GEOKA, RS2 BACSU, RS2_LACAC}:
Видим следующее: d(ENTFA,GEOKA)+d(BACSU,LACAC)=0.33458+0.48115=0,81573,
d(ENTFA,LACAC)+d(GEOKA,BACSU)=0.48115+0.12266=0,60381, d(ENTFA,BACSU)+d(GEOKA,LACAC)=0,33458+0.48115=0,81573.
Получилось, что две суммы абсолютно равны между собой и больше третьей, что говорит о выполнении свойства аддитивности.
Таким образом, сравнивая эти значения со значениями дерева по fprotpars, ясно видно, что последние две реконструкции
намного вернее.