Приближение синуса квадратным трёхчленом

Одним из заданиев практикума, связанного с изучением возможностей Microsoft Excel, было создание таблицы, при вводе в котору. некоторых чисел a, b и c из отрезка [0;π], строился бы график квадратного трёхчлена, аткой, что в этих точках он принимает значения, равные sin(a), sin(b) и sin(c). Для этого нужно решать следующую систему линейный уравнений:

A*(a)^2 + B*(a) + C = sin(a)
A*(b)^2 + B*(b) + C = sin(b)
A*(c)^2 + B*(c) + C = sin(c)

Где A, B и C - это коэффиециенты в квадратном трёхчлене. Эту систему можно решить, с помощью матрицы

a^2 a 1 | sin(a)
b^2 b 1 | sin(b)
c^2 c 1 | sin(c)

Методом Краммера. Отсюда однозначно определяются коэффиециенты A, B, C и можно построить график соотвествующей функции. Используя различные варианты вводимых a, b и c были получены следующие графики:

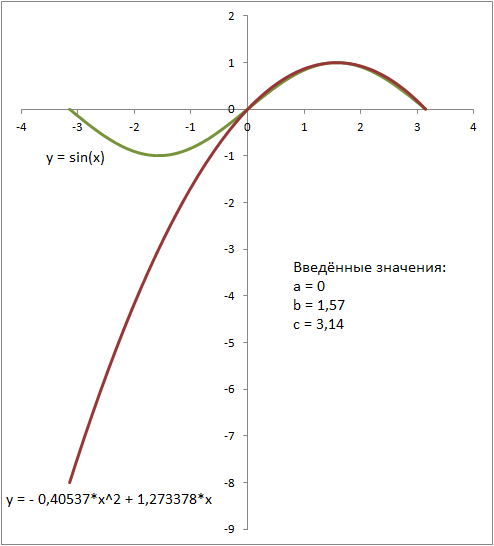Рис.1. приближение квадратного трёхчлена к синусу. Красным цветом показан график тнрёхчлена, зелёным - синуса. Введённые значения: a = 0, b = 1,57 c = 3,14

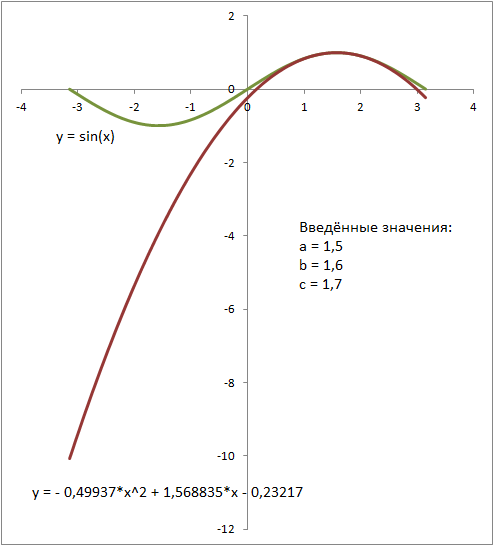Рис.2. приближение квадратного трёхчлена к синусу. Красным цветом показан график тнрёхчлена, зелёным - синуса. Введённые значения: a = 1,5, b = 1,6 c = 1,7

Из графиков на рисунке 1 и рисунке 2 видно, что если значения a, b и c взять с сильным разбросом (из начала отрезка, середины и конца) или с небольшим разросом, но в центре заданного отрезка, тографик квадратного трёхчлена на заданном отрезки очень похож на график синуса.

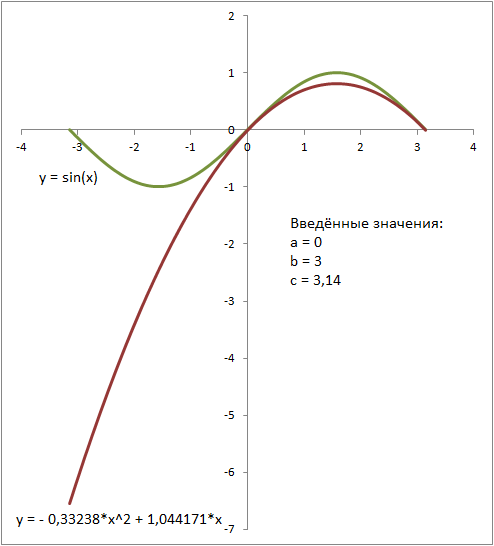Рис.3. приближение квадратного трёхчлена к синусу. Красным цветом показан график тнрёхчлена, зелёным - синуса. Введённые значения: a = 0, b = 3 c = 3,14

Если взять значения параметров только с концов отрезков, как на рисунке 3, то график уже довольно сильно отличается от графика синуса, особенно сильно различие в середине отрезка.

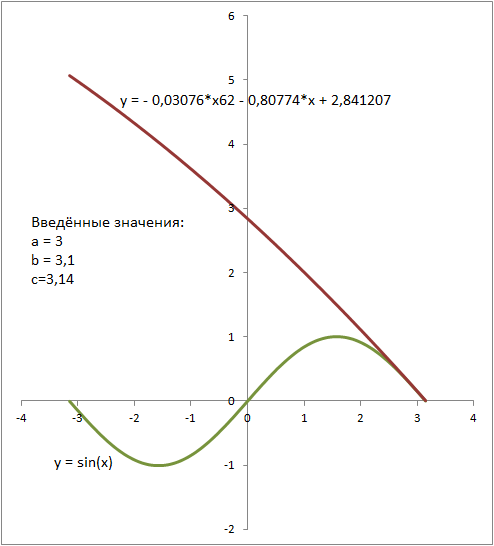Рис.4. приближение квадратного трёхчлена к синусу. Красным цветом показан график тнрёхчлена, зелёным - синуса. Введённые значения: a = 3 b = 3,1 c = 3,14

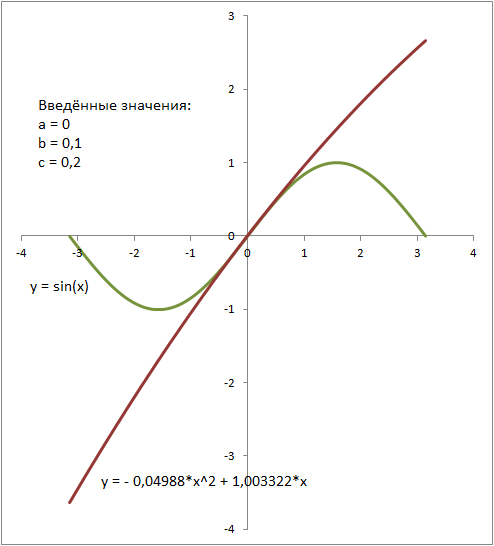Рис.5. приближение квадратного трёхчлена к синусу. Красным цветом показан график тнрёхчлена, зелёным - синуса. Введённые значения: a = 0 b = 0,1 c = 0,2

А если точки взять с небольшим разбросом и на концах отрезка, как на рисунке 4 и рисунке 5, то график такой функции приближается к касательной графика sin(x).