Укоренение в среднюю точку
Для реконструкции филогенетического дерева мною был выбран белок с мнемоникой RF1,
являющийся фактором высвобождения пептидной цепи 1.
Из Swiss-Prot были получены
последовательности белков с данной функцией из отобранных ранее бактерий. Программой Muscle
было построено их выравнивание (ссылка на выравнивание в fasta-формате).
Для удобства от названия белка в выравнивании была оставлена только мнемоника вида.
 |
| Рис. 1. Выравнивание белковых последовательностей выбранных бактерий |
Методом "Neighbor Joining Using % Identity" было реконструировано филогенетическое дерево (ссылка на дерево в Newick-формате).
Ссылка на проект JalView
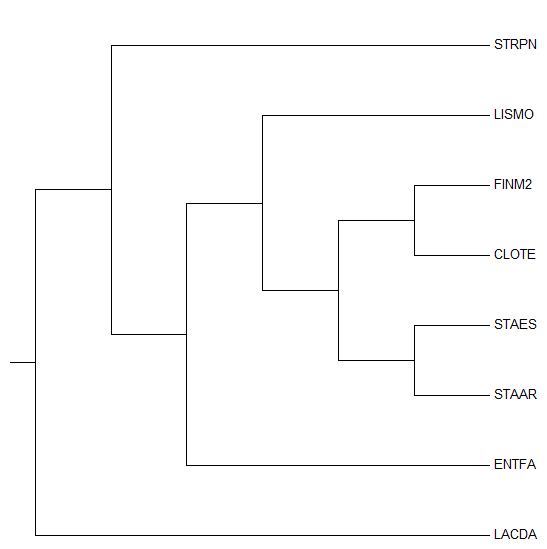
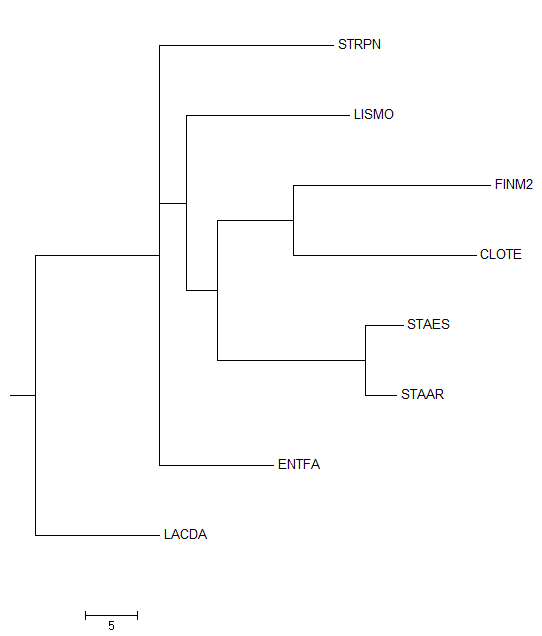
Полученное с помощью JalView дерево было открыто в программе Mega (с сохранением длин ветвей и без). Изображения данных деревьев можно увидеть ниже.
 |
 |
| Рис.2. Дерево, построенное JalView, открытое в Mega без учета длин ветвей |
Рис.3. Дерево, построенное JalView, открытое в Mega с учетом длин ветвей |
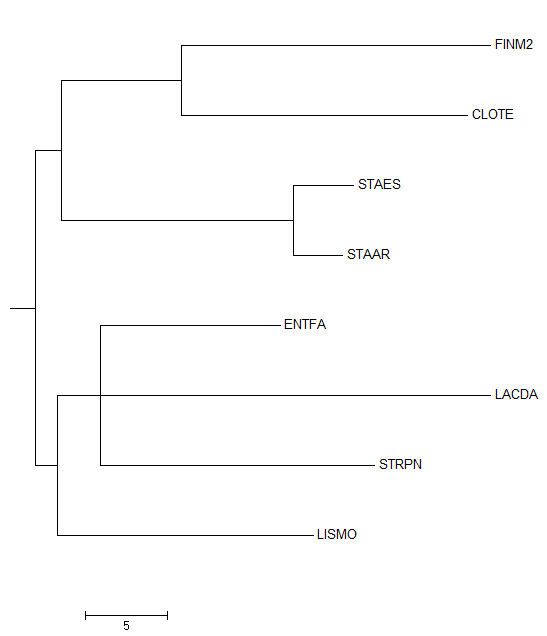
Затем данное дерево было переукоренено в среднюю точку с помощью программы retree пакета PHYLIP (выходной файл outtree). Ниже можно увидеть построенные Mega изображения полученного дерева.
 |
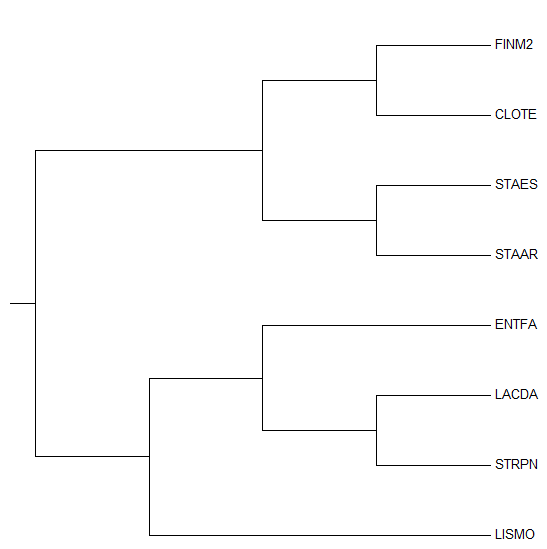 |
| Рис. 4. Дерево, переукорененное в среднюю точку, с длинами ветвей | Рис. 5. Дерево, переукорененное в среднюю точку, без длин ветвей |
Можно заметить, что когда мы строим наше дерево с учетом длин ветвей, оно и до, и после переукоренения получается небинарным. При построении без учета длин эта проблема пропадает. Поэтому сначала будут описаны изображения деревьев без учета длин.
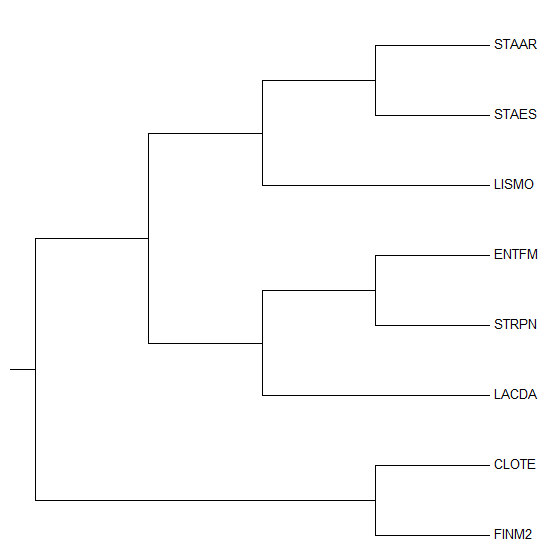 |
| Рис.6. Эталонное дерево |
- {FINM2, CLOTE} против {STAAR, STAES, LISMO, ENTFA, STRPN, LACDA}
- {STAAR, STAES} против {LISMO, ENTFA, STRPN, LACDA, CLOTE, FINM2}
- {FINM2, CLOTE, STAAR, STAES} против {LISMO, ENTFA, STRPN, LACDA}
- {FINM2, CLOTE, STAAR, STAES, LISMO} против {ENTFA, STRPN, LACDA}
- {FINM2, CLOTE, STAAR, STAES, LISMO, ENTFA} против {STRPN, LACDA}
В свою очередь, в нашем дереве нет ветвей {ENTFA, STRPN} против {STAAR, STAES, LISMO, CLOTE, FINM2, LACDA} и {STAAR, STAES, LISMO} против {ENTFA, STRPN, LACDA, CLOTE, FINM2}.
Тем не менее, если рассматривать неразрешенное дерево, посроенное с учетом длин, то можно заметить, что среди возможных его разрешений существует вариант, в котором ветвь {ENTFA, STRPN} против {STAAR, STAES, LISMO, CLOTE, FINM2, LACDA} появляется.
Дерево, переукорененное в среднюю точку, содержит те же ветви, что и изначальное, что, собственно, логично. Соответственно, оно так же, как и изначальное, отличается от эталонного. Укоренено новое дерево в ветвь {FINM2, CLOTE, STAAR, STAES} против {LISMO, ENTFA, STRPN, LACDA}. На первый взгляд такое укоренение кажется возможным, однако в эталонном дереве этой ветви нет, и правильность укоренения вызывает сомнения.
Укоренение в среднюю точку можно произвести только при учете длин ветвей. Полученное нами дерево с длинами ветвей является небинарным. Среди вариантов возможных разрешений есть такие, которые в большей или меньшей степени совпадают с эталонным деревом. Как и в предыдущем случае, можно построить такое разрешение, в котором будет присутствующая в эталонном ветвь {ENTFA, STRPN} против {STAAR, STAES, LISMO, CLOTE, FINM2, LACDA}.
Использование внешней группы
Метод максимальной экономии ("Maximum parsimony") не учитывает длины ветвей, поэтому укоренение в среднюю точку
провести нельзя. В таком случае можно использовать укоренение с помощью внешней группы.
Для укоренения дерева белков отобранных бактерий в качестве внешней группы был использован белок
тогоже семейства из Escherichia coli (RF1_ECOLI). К файлу с невыровненными
последовательностями белков фирмикут была добавлена последовательность белка
Escherichia coli, после чего последовательности были выровнены Muscle.
Ссылка на JalView проект
Выравнивание в формате fasta
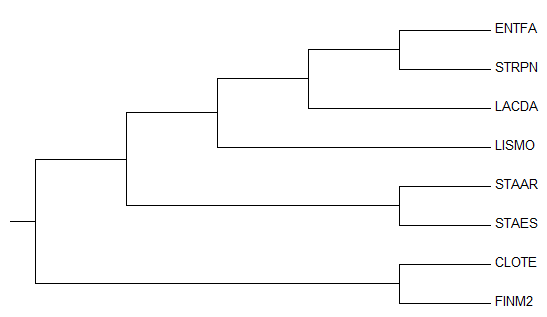 |
| Рис.7. Дерево, укорененное методом внешней группы |
Укорененное таким способом дерево по топологии более близко к эталонному. В нем есть почти все те же ветви (4 из 5 совпадают), различие только в положении LISMO. Поэтому в случае с отобранными мной бактериями укоренение с помощью внешней группы можно назвать более правильным, чем укоренение в среднюю точку.
Bootstrap
Бутстрэп (англ. bootstrap, петля на заднике ботинка) - непараметрический метод статистики,
основанный на многократной генерации выборок
методом Монте-Карло на базе имеющейся выборки.
В случае с построением деревьев из входного выравнивания создается много так называемых
«бутстрэп-реплик», каждая их которых получается в результате случайного удаления половины
столбцов из выравнивания с заменой их копиями других случайно выбранных столбцов. Для каждой
из реплик строится дерево, а затем из всех этих деревьев строится одно по методу
расширенного большинства («Extended majority-rule tree»). Сначала строится дерево из ветвей,
встретившихся в большинстве исходных деревьев, а потом к нему добавляются ветви, не
противоречащие уже имеющимся, начиная с наиболее «поддержанных».
C помощью программы Mega я провела бутстрэп-анализ филогении отобранных белков с чилом реплик,
равным 100. Original Tree было построено методом Neighbour Joining. Ниже можно увидеть изображения
обоих полученных в ходе анализа деревьев.
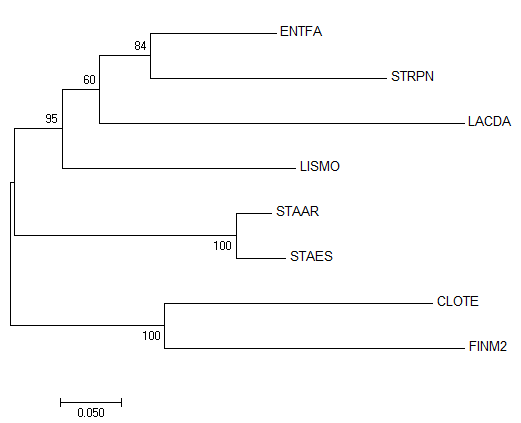 |
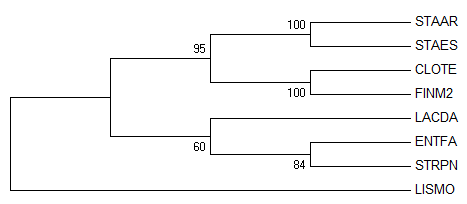 |
| Рис. 8. Оригинальное дерево, построенное методом Neighbour Joining | Рис. 9. Консенсусное дерево на основе бутстрэп анализа |
По топологии Original tree и Bootstrap consensus tree совпадают. Они имеют по 5 нетривиальных ветвей:
- {FINM2, CLOTE} против {STAAR, STAES, LISMO, ENTFA, STRPN, LACDA}
- {STAAR, STAES} против {LISMO, ENTFA, STRPN, LACDA, CLOTE, FINM2}
- {FINM2, CLOTE, STAAR, STAES} против {LISMO, ENTFA, STRPN, LACDA}
- {FINM2, CLOTE, STAAR, STAES, LISMO} против {ENTFA, STRPN, LACDA}
- {FINM2, CLOTE, STAAR, STAES, LISMO, LACDA} против {STRPN, ENTFA}