Восстановление функции ЭП по ряду Фурье

Задание состоит из 4-х этапов:

Смоделировать функцию электронной плотности (ЭП)
Рассчитать гармоники
Восстановить ЭП по смоделированной функции
Оценить качество восстановления

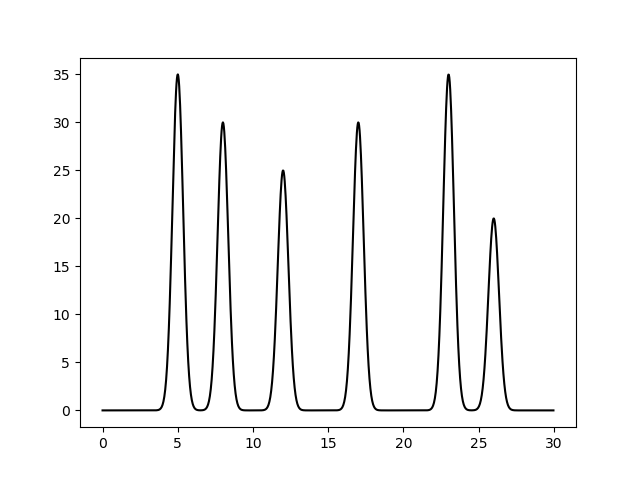
Моделирование функции

Для моделирования использовался файл variant8.txt с набором пар {x;y} и характеристиками гауссовых функций, использовавшимися в качестве параметров скриптом compile-func.py:
compile-func.py -g 35,2,5+30,2,8+25.0,2,12+30.0,2,17+35.0,2,23+20,2,26
Результатом работы скрипта стал файл func.txt с набором значений функции электронной плотности, смоделированной по сумме гауссовых функций.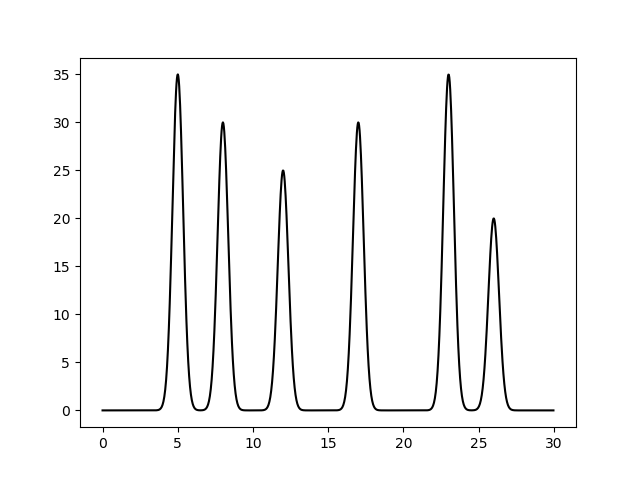

Рис. 1 Смоделированная функция электронной плотности

Рассчёт гармоник

Ряд Фурье представляет собой сумму гармоник. Каждая гармоника характеризуется порядком (определяет период гармоники), амплитудой (коэффициент перед косинусом) и фазой (прибавка к аргументу косинуса). Для получения гармоник смоделированная функция разложена в ряд Фурье с помощью скрипта func2fourier.py:
func2fourier.py -i func.txt -o fu2fo_garm.txt
На выходе получился файл fu2fo_garm.txt с наборами {порядок; амплитуда; фаза} - всего 499 гармоник.

Восстановление ЭП

Восстановление велось с помощью скрипта fourier2func.py.

Восстановление по полному набору

Для восстановления ЭП можно взять полный набор гармоник - все 499 штук из файла fu2fo_garm.txt
`fourier2func.py -i fu2fo_garm.txt -o full_garm_rcvr.txt -s`
В итоге восстановленная функция ничем не будет отличаться от смоделированной:

Смоделированная функция (func.txt) Восстановленная функция (full_garm_rcvr.txt)

Минимальный полный набор гармоник

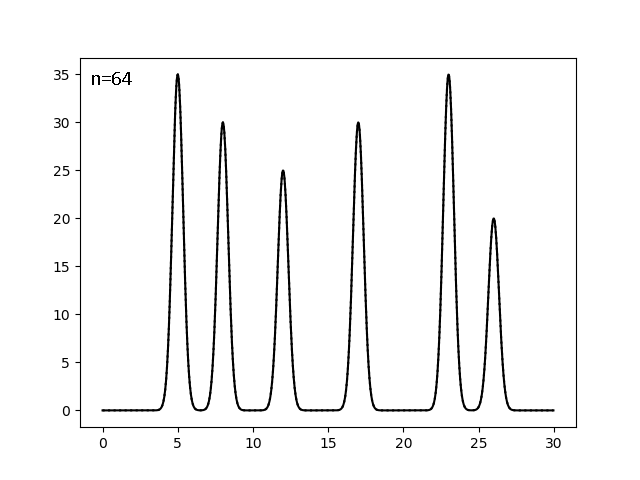
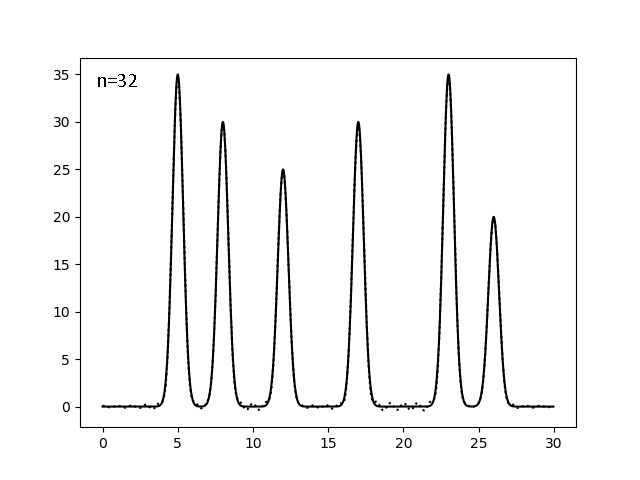
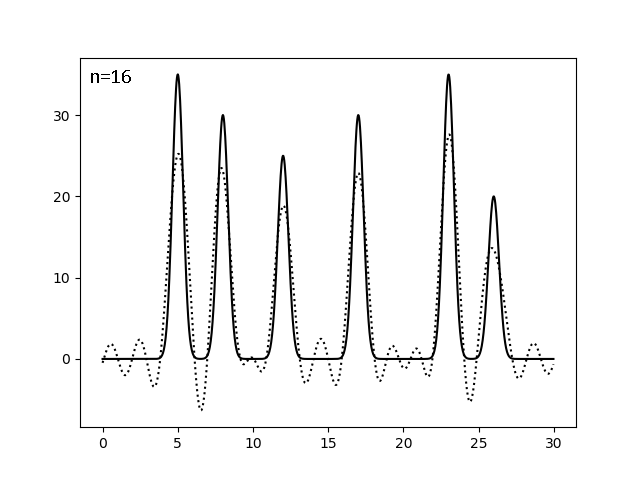
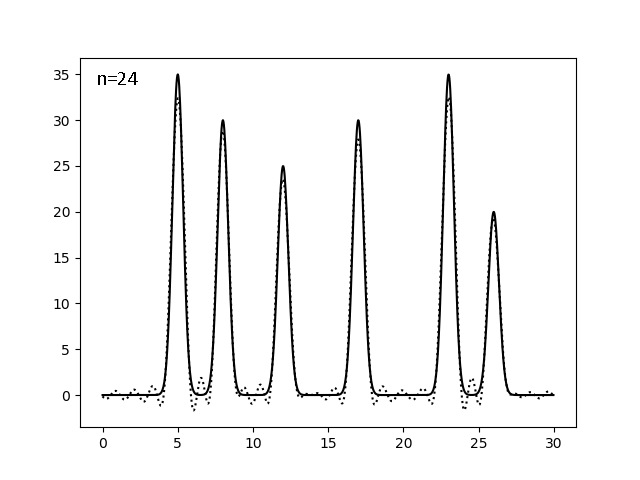
Найдём минимальный полный набор гармоник, на котором реализуется отличное (можем определить положения всех максимумов) восстановление. Для этого оставляем с помощью скрипта fourier-filter.py гармоники с 0 до n включительно и смотрим, рисуя скриптом fourier2func.py, на каком n можно остановиться. Поиск шёл дихотомически, при n=256,128,64...:


fourier-filter.py -i fu2fo_garm.txt -r 0-256 -o garm_0to256.txt #для файла с гармониками с 0 по 255

fourier2func.py -i garm_0to256.txt -o func_0to256.txt

Результаты в порядке получения:

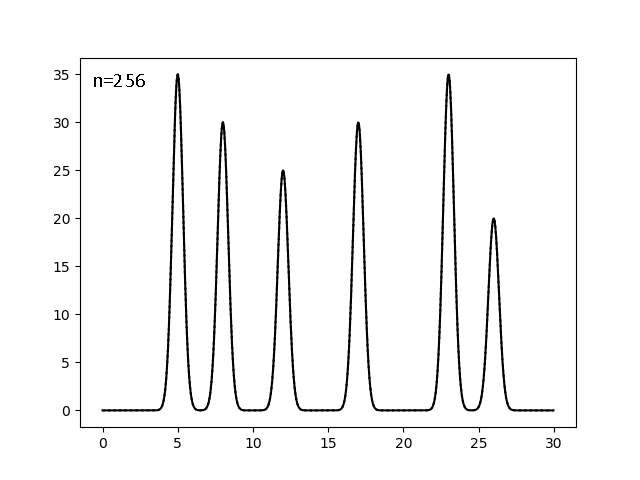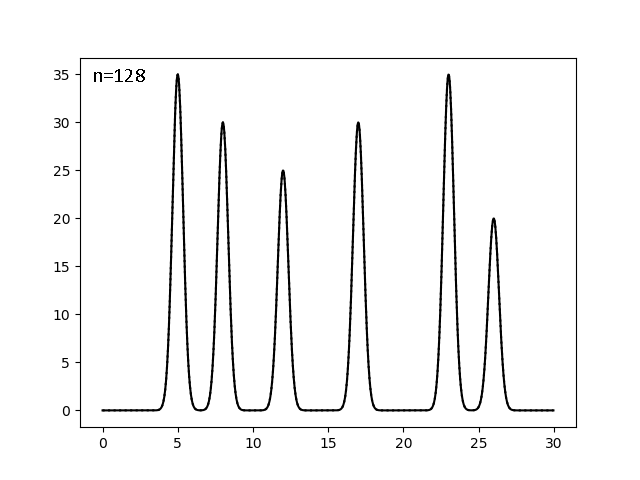Видно, что с уходом в 16 гармоник функция восстанавливается совсем плохо, а 32 гармоники уже не оставляют сомнений в её форме. При n=28 восстановление всё ещё видимо пляшет, но n=30 не сильно разнится с n=32, поэтому примем 30 за n₀. Результат ожидаем, так как период гармоники с номером 30 на расстоянии в 30Å как раз описывает детали размером 1Å

Влияние искажений фазы и амплитуды

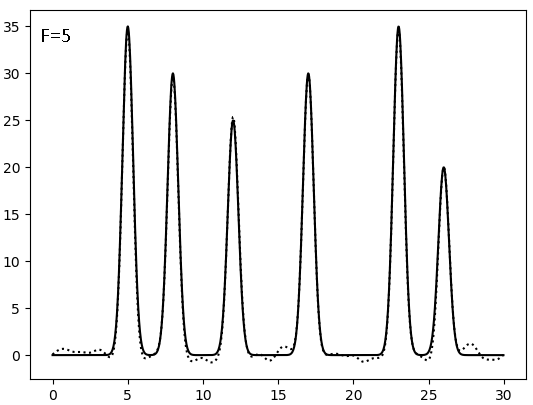
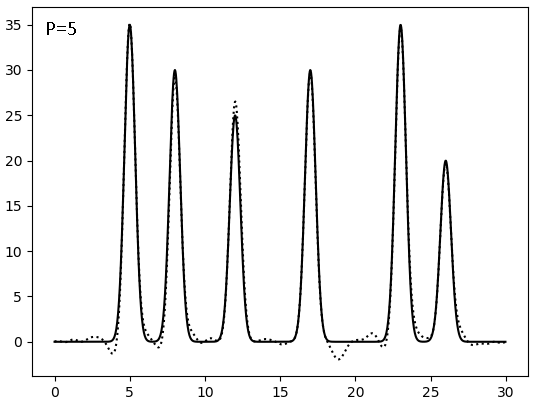
Теперь на минимальном полном наборе оценим влияние искажений значений фазы и амплитуды. Шумы вносятся при построении функции скриптом func2fourier.py:

func2fourier.py -i func.txt -o func_f5p5.txt -F 5 -P 5 #Шум по амплитуде - 5%, шум по фазе - 5%

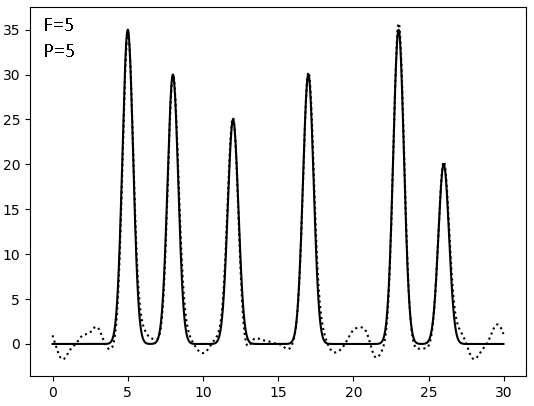
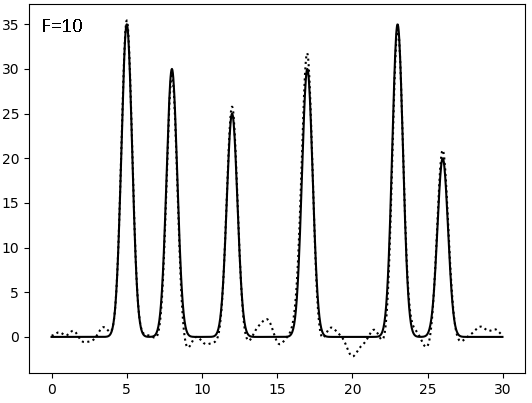
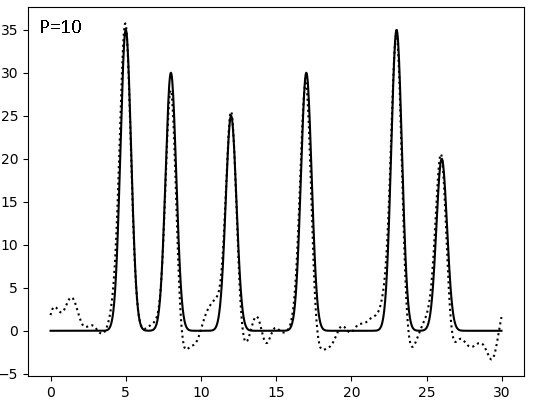
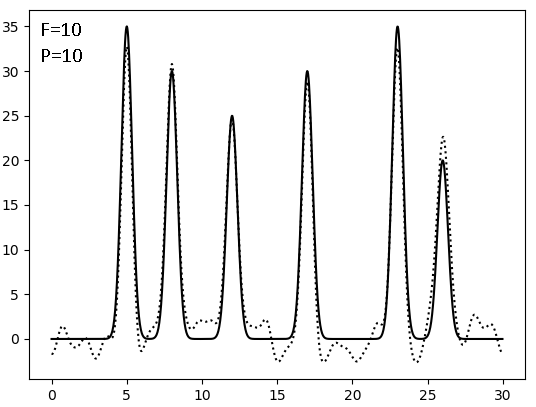
Результаты восстановления после внесения искажений (F - по амплитуде, P - по фазе, сплошная линия - исходная функция, точковая - результат искажений):

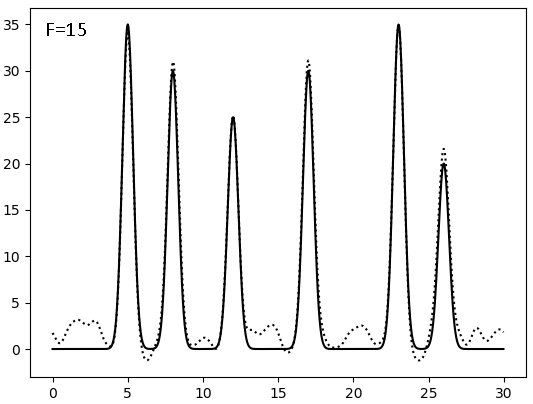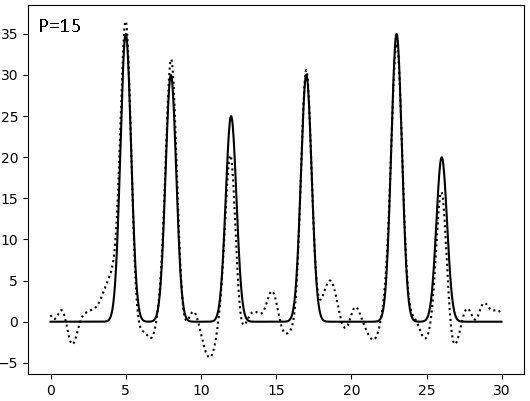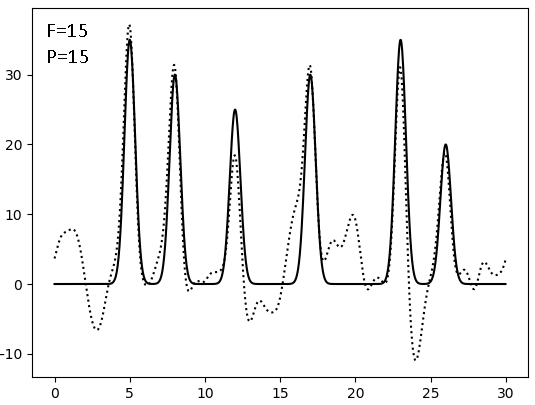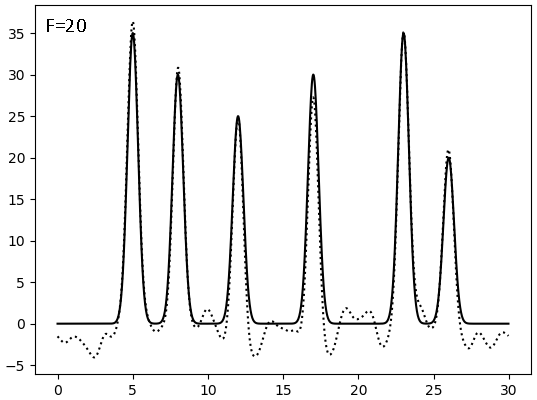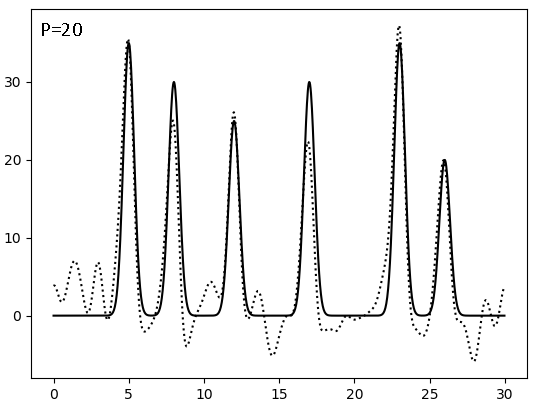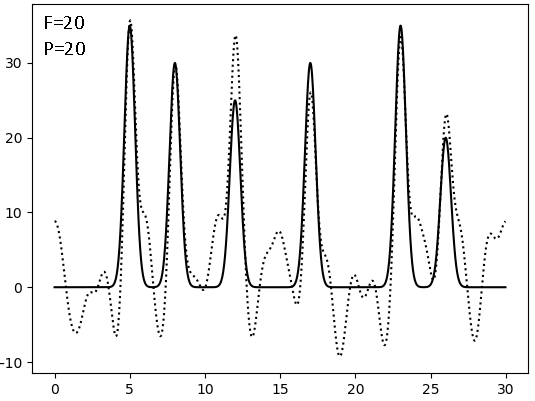Видно, что плохим качество восстановления становится при соотношении сигнал/шум = 4, то есть после 20% искажений. И фаза гораздо значимее влияет на восстановление, чем амплитуда - а ведь именно фазу мы получаем косвенным метдом, а не прямым измерением.

Восстановление при неполном наборе гармоник

Работаем на минимальном наборе 0...n₀. На этот раз просто выпиливаем гармоники руками в файле. Результаты - в таблице:

Убраны первая и нулевая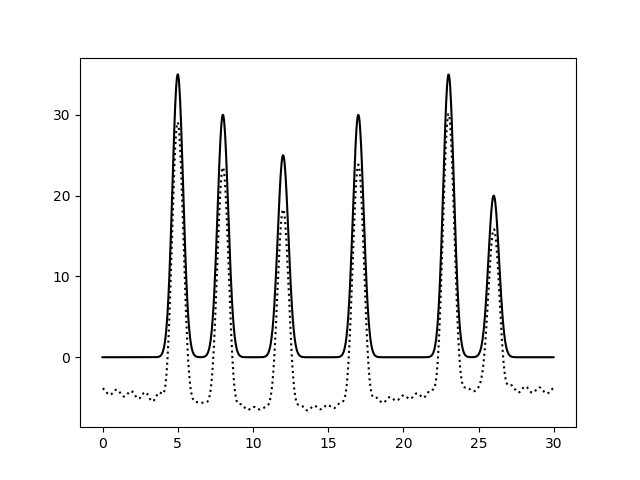
Без трёх гармоник подряд в первой трети(№10, 11, 12)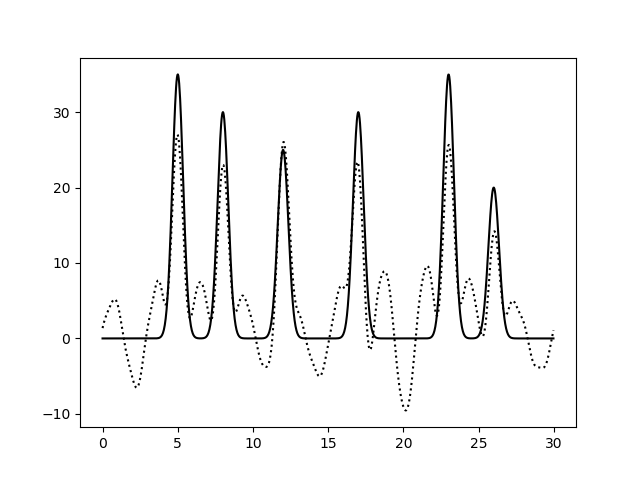
Без трёх гармоник подряд во второй трети(№21, 22, 23)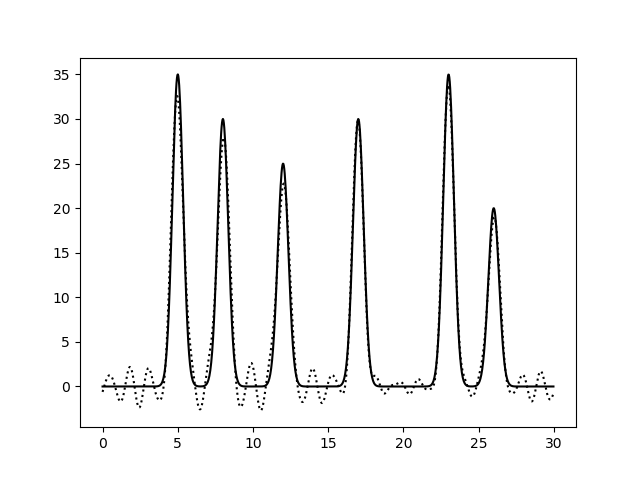
Отсутствие гармоник равномерно (без № 8, 16 и 24)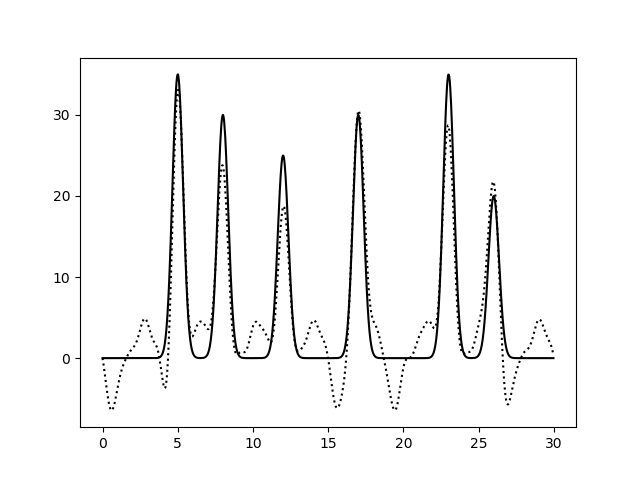
к 30 минимальным добавлена ещё одна (№40)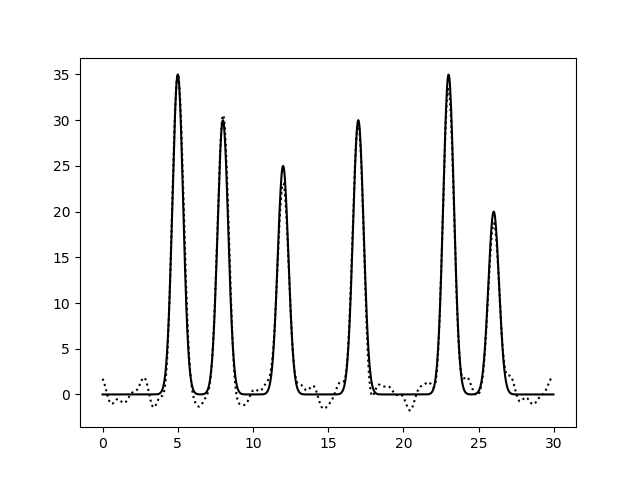

Хуже всего сказывается отсутствие гармоник первого-второго десятков, хотя нулевая и первая гармоники почти не влияют на различимость пиков - только на уровень "нуля". При этом равномерны ли прорехи в гармониках или скучены - не важно. Забавно, что одна лишняя гармоника вносит искажения, поскольку формально получается ряд с пропущенными 9ю членами.

Оценка качества восстановления при разных условиях

Разрешение оценивается как отношение длинны участка к числу гармоник, в нашем случае длина составляла 30Å.Полнота данных определяется как отношение числа имеющихся для восстановления функции гармоник к числу их в полном наборе (то есть к n, если полный набор - от 0 до n)

Набор гармоник	Разрешение,Å	Полнота данных, %	Шум по амплитуде, %	Шум по фазе,%	Качество восстановления
0-498	0,06	100	0	0	Отл
0-256	0,12	100	0	0	Отл
0-125	0,24	100	0	0	Отл
0-64	0,47	100	0	0	Отл
0-32	0,98	100	0	0	Отл
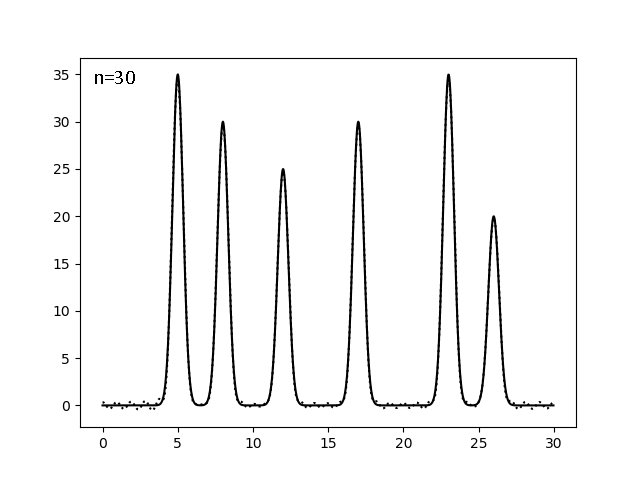
0-30	1	100	0	0	Отл
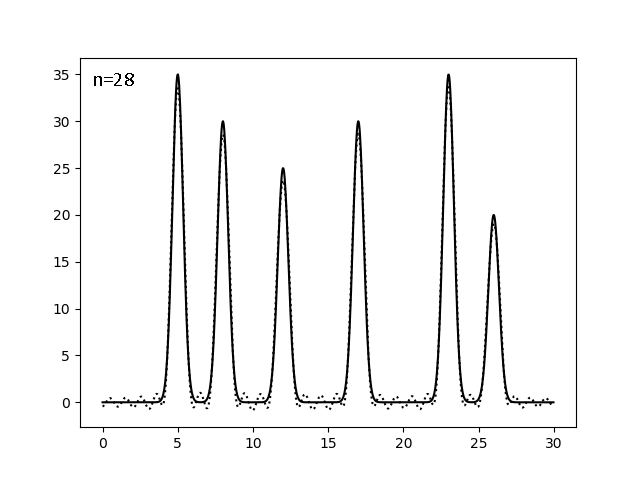
0-28	1,07	100	0	0	Хор
0-24	1,25	100	0	0	Хор
0-16	1,88	100	0	0	Плох
0-30	1	100	5	0	Отл
0-30	1	100	0	5	Хор
0-30	1	100	5	5	Хор
0-30	1	100	10	0	Хор
0-30	1	100	0	10	Хор
0-30	1	100	10	10	Хор
0-30	1	100	15	0	Хор
0-30	1	100	0	15	Хор
0-30	1	100	15	15	Плох
0-30	1	100	20	0	Хор
0-30	1	100	0	20	Плох
0-30	1	100	20	20	Плох
2-30	1,07	97,5	0	0	Отл
0-9,13-30	1,11	90	0	0	Плох
0-20,24-30	1,11	90	0	0	Хор
0-7,9-15,17-23,25-30	1,1	90	0	0	Хор
0-30,40	0,98	100	0	0	Отл