Оптимальное парное выравнивание. Алгоритмы.

1. Сравнение глобального и локального выравниваний для белков A1UA31.1 и P22953.3

Для глобального и локального выравниваний этих белков использовались команды needle и water пакет EMBOSS со стандартными параметрами Gap penalty: 10.0, Extend penalty: 0.5, End penalty: 10.0, end extend penalty:0.5. Программой по умолчанию используется матрица весов EBLOSUM62 (для белковых послеовательностей).

Таблица 1. Сравнение параметров локального и глобального выравниваний

Выравнивание	Длина выравнивания	Гэп	Гэп, %	Identity abs	Identity percent	Similarity abs	Similarity percent	Число инделей	Вес выравнивания
needle	673	73	10.8%	300	44.6%	412	61.2%	7	1361.0
water	647	54	8.3%	297	45.9%	409	63.2%	13	1365.5

При глобальном выравнивании предполагается, что последовательности гомологичны по всей длине, а при локальной, что белки содержат как гомологичные домены, так и нет, и можно перейти в любое место последовательности без штрафа. В нашем случае локлаьное и глобальное выравнивание различаются только в N- и С- концах последовательности (см. рисунок 1). И это неудивительно, ведь белок A1UA31.1 принадлежит представителю домена Бактерии, а P22953.3 - Эукариотам, и N- и С-концы, обычно служащие маркерами локализации белков в клетке (или связывания с сигнальными молекулами), у них различаются. (Примечательно, что сначала я пыталась работать с одним белком представителя Архей, а другим- Бактерий и в этом случае локальное и глобальное выравнивания совпали, что свидетельствует о бОльшей консервативности этих белков между Бактериями и Археями, чем Бактерий и Эукариот).

2. Сравнение локального выравниваний для негомологичных белков

Для выполнения этого задания я использовала локального выравнивание двух гомологичных белков из задания 1 и 5 пар выравниваний заведомо негомологичных белков (своего белка Q816E8_BACCR, репарирующего алкилированные основания [1] с белками A0A0U3M8E6_9BURK, хитиназой [2], E8YFS1_9BURK, гликозил-трансферазой [3], A0A0H4VDW6_9SPHN, белком-регулятором клеточного деления [4], NHAA_RHOER, субъединицей нитрил-гидратазы [5] и Q82CH9_STRAW, глобин-подобным белком [6]). В таблице 2 приведены основные параметры этих выравниваний.

Таблица 2. Сравниения локальных выравниваний 5 пар негомологичных белков

Идентификатор белка	Длина выравнивания	Гэп	Гэп, %	Identity	Identity,%	Similarity	Similarity,%	Число инделей	Вес выравнивания
A0A0U3M8E6_9BURK	32	3	9.4%	8	25.0%	17	53.1%	2	29.5
E8YFS1_9BURK	102	29	28.4%	20	19.6%	35	34.3%	4	29.5
A0A0H4VDW6_9SPHN	109	16	14.7%	21	19.3%	44	40.4%	4	45
NHAA_RHOER	7	0	0%	6	85.7%	6	85.7%	0	27.0
Q82CH9_STRAW	29	4	13.8%	9	31.0%	15	51.7%	2	30.0

На рисунке 2 представлены изображения локальных выравниваний негомологичной пары (выше) и гомологичной (ниже).
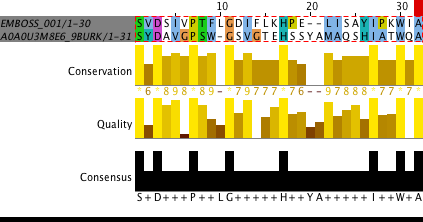
Если сравнить данные из таблиц 1 и 2, то можно заметить, что при локальном выравнивании негомологичных белков длина выровненного участка значительно меньше, чем в случае гомологичной пары (по 30-100 нуклеотидов вместо обычных 600). Также интересно заметить, что программа гораздо дольше (несколько секунд) строила выравнивание негомологичных пар. Очевидно, что такому выравниванию верить нельзя и найденные программой якобы гомологичный участок между двумя белками является случайностью. Если говорить в общем, то на мой взгляд выравнивание негомологичны белков лишено смысла и абсолютно неинформативно.

3. Отличия между выравниваниями

Я выбрала выравнивания, описанные в задании 1 между белками A1UA31.1 и P22953.3. Выбранные выравнивания практически полностью совпали, за исключением начальных и конечных участков. Отличия. В множественном выравнивании напротив Met1 стоит Met1, а в глобальном выравнивании напротив Met1 стоит Glu6. В множественном выравнивании напротив Ala2 стоит Ser2, а в глобальном напротив Ala2 стоит Gly7. Напротив Thr83 стоит Arg, а в глобальном выравнивании напротив него стоит Ser7. Рисунок выравнивания приведен ниже. Видно, что выравнивания, в основном, отличаются на концевых участках. Интересно, что выравнивания в гомологичных блоках совпадают, а в негомологичных участках различаются (разные программы ставят разное количество гэпов). В случае данных белков глобальное и локальное по информативности не отличаются (тк эти белки довольно консервативны и содержат гомологичые блоки по всей длине. Глобальное и множественное выравнивание отличаются, в основном количеством гэпов в неконсервативных участках (в множественном их больше).

4. Описание глобального выравнивания с аффинными штрафами за гэпы

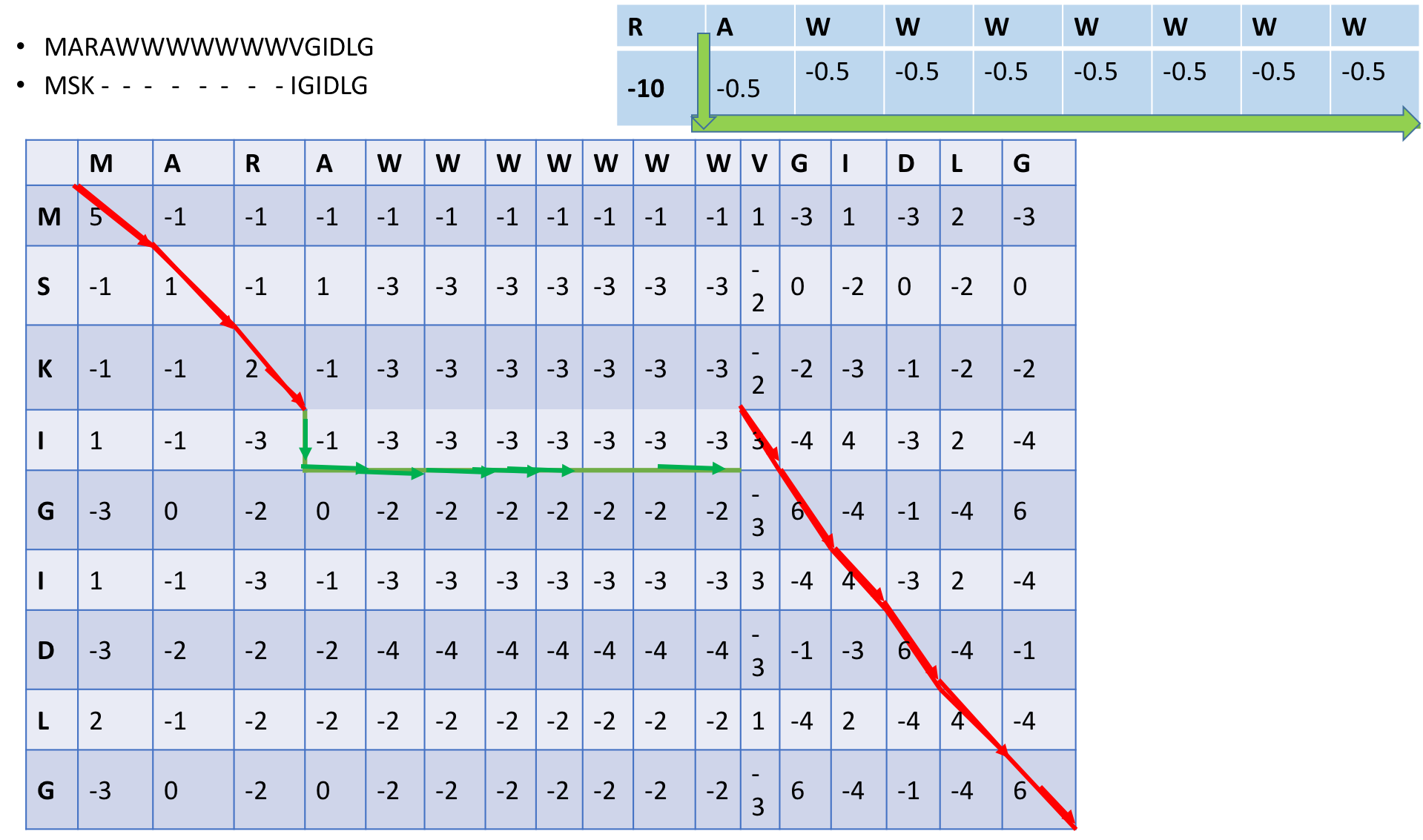
Выравняем кусочек последовательности MARAWWWWWWWVGIDLG и MSKIGIDLG. На рисунке 4 представлены матрицы значений. Представим, что большая матрица с аминоксилотами представляет собой верхнюю грань параллелепипеда, в каждой ячейке написан вес замены (матрица BLOSUM62), а маленькая -вертикальный срез между двумя конкретными строками (спуск по грани этих ячеек: штраф 10, прохождение по этой ячейке- штраф 0.5, подъем наверх - 0). Сначала двигаемся по верхней грани по диагоналям ячеек (так как это наиболее выгодно по весам), как только мы проходим ячейку R-K, то перед нами встает выбор: продолжать двигаться по верхней грани или спуститься вглубь. Рациональнее будет потратить 10 очков, на "спуск в метро" и пройти "плохой" участок со штрафами в 0.5 за ячейку, чем оставться на верхней грани, где штрафы -3 -2. Красным цветом отмечено движение по верхней грани, зеленым - по " внутренней" части, как вертикальный разрез. После прохождения последнего триптофана можно "подняться наверх" и продолжить движение по диагонали. Итого вес выравнивания: 5+1+2 -10 - (0,5*7)+3+6+4+6+4+6=23.

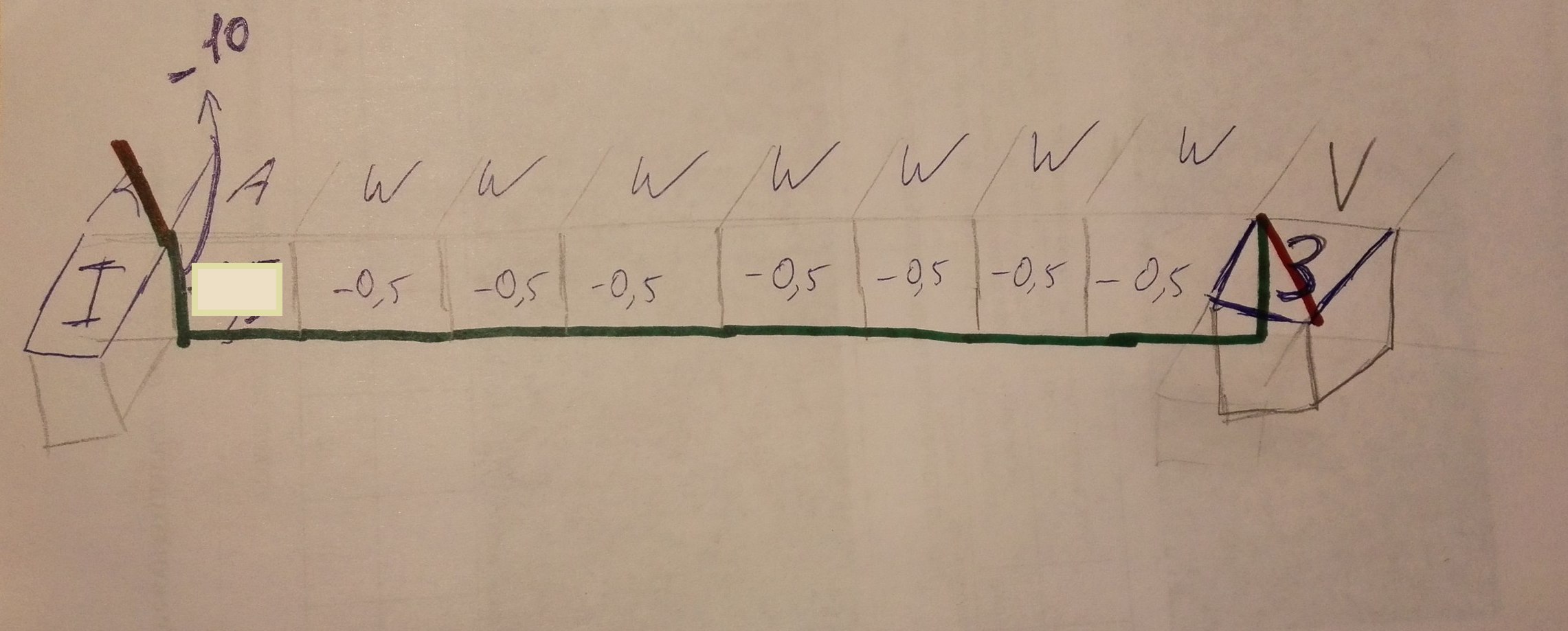
5. Описание локального выравнивания с линейными штрафами за гэпы

Выравниваются те же участки последовательности, что и в задании 4. Отличием локального от глобального выравнивания является то, что из любой точки можно "перескочить" в любую без штрафа. Таким образом можно "выбросить" негомологичные кусочки. Что и происходит в нашем примере. Если посмотреть на рисунок , можно увидеть, что сначала мы двигаемся как и в предыдущем задании, затем доходим до негомологичного участка, перемещаемся в гомологичный и двигаемся до конца. Результатом выравнивания является 2 попарно гомологичных кусочка последовательностей. В данном случае выгоднее было не вставлять 8 гэпов (штрафы за них бы линейно суммировались), а перескочить негомологичный участок. Вес выравнивания : 1 кусочек 5+1+2 =7 , 2 кусочек 3+6+4+6+4+6=28.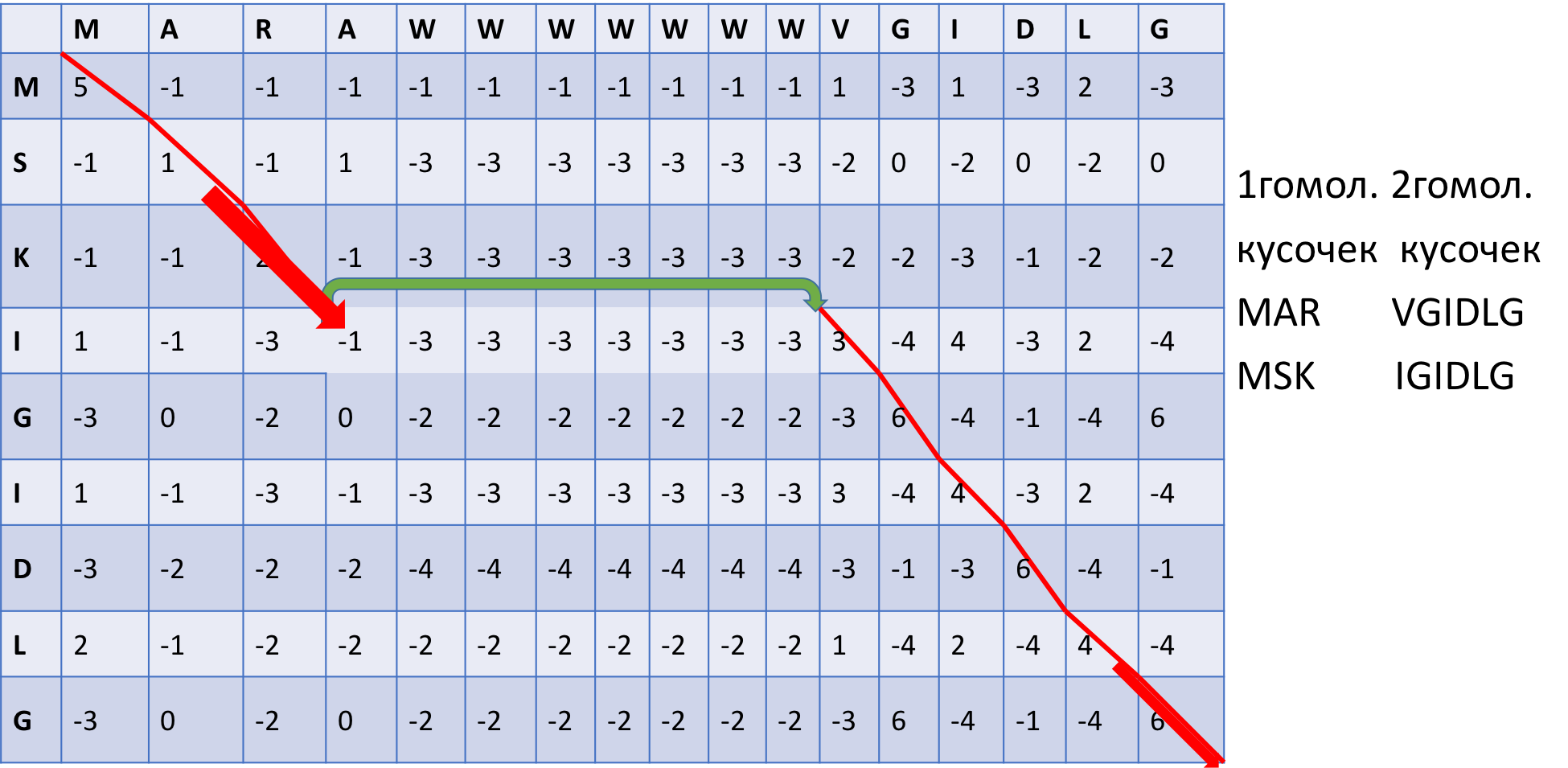

6. Составление матрицы "весов дружелюбности"

Для выполнения этого задания я пользовалась матрицей Редхеффера. Число возможных пар:132, итоговые значения умножались на 10.

Таблица 3. Матрица весов для матрицы Редхеффера

	1	0	Сумма
1	-16,1	-9	-25,1
0	-10,8	9,8	-1
Сумма	-26,9	18,8

7. Список литературы

[1] http://kodomo.fbb.msu.ru/~azbukinanadezda/term2/pr4/pr4.html
[2] http://kodomo.fbb.msu.ru/~kamikki0/term_2/practicum3.html
[3] http://kodomo.fbb.msu.ru/~sergebus/term2/prak5.html
[4] http://kodomo.fbb.msu.ru/~buyanchik/term2/pr5/uniprotinf.html
[5] http://kodomo.fbb.msu.ru/~liliavasilyeva/pr5.html
[6] http://kodomo.fbb.msu.ru/~sophia.veselova/term2/pr5/uniprot.html