Практикум 8
Сигналы в геноме
Задание 2
В первом семестре, на курсе по Python, мы однажды искали самые распространенные 6-меры в 20 нуклеотидах перед старт-кодоном в геномах трех бактерий: E. coli, Mycoplasma pneumoniae и некоторой Cand. Gracilibacteria (практикум 13, задание 6). Этот практикум напомнил мне о том задании, и я решил вернуться к получившимся тогда результатам.
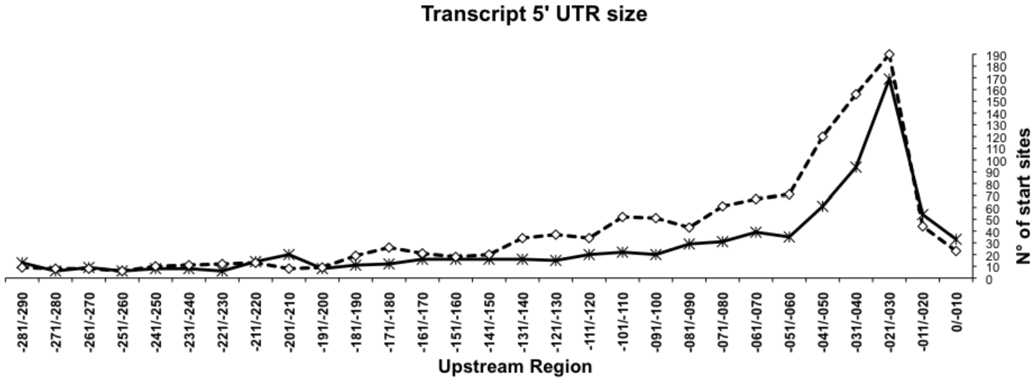
Самыми распространенными оказались два типа 6-меров: напоминающие последовательность Шайна — Дальгарно (в геноме E. coli) или состоящие только из A и T (в геноме Gracilibacteria). У M. pneumoniae среди самых распространенных оказались и те, и другие. Тогда я решил (видимо, ошибочно), что AT-последовательности — это Прибнов-бокс. На самом деле точка начала транскрипции расположена дальше от старт-кодона (рис. 1). Для большинства мРНК 5'-UTR имеет длину 20–40 нуклеотидов, а так как Прибнов-бокс расположен еще на 10 нуклеотидов дальше, он может попасть в ближайшие 20 нуклеотидв к старт-кодону только для генов с самым коротким UTR, судя по рис. 1 в геноме E. coli таких около 30 (да, нас интересует не E. coli, а наоборот другие бактерии, но порядок чисел, я думаю, такой же).
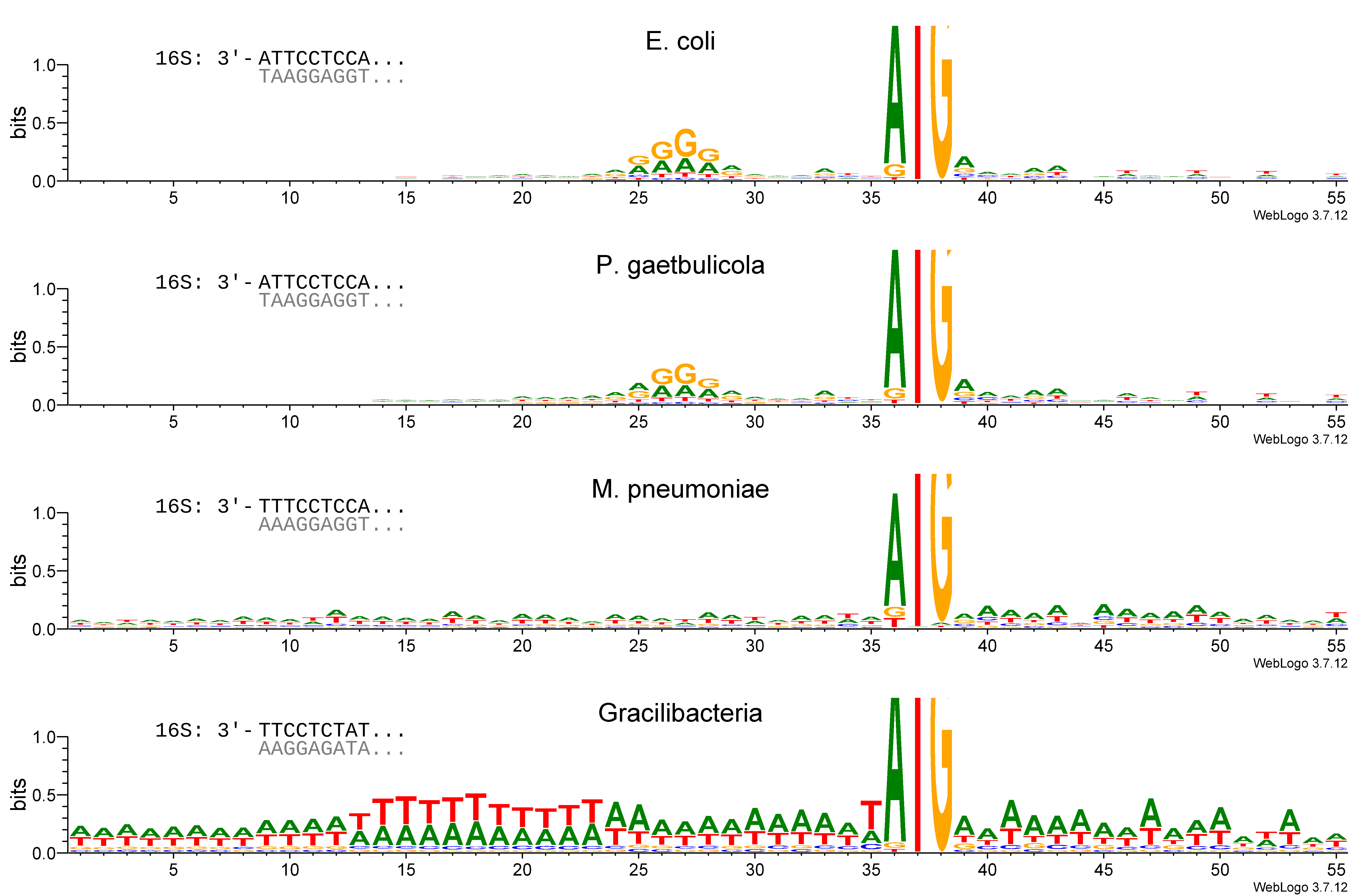
Сначала я решил просто посмотреть с помощью лого на то, как выглядят окрестности старт-кодона у этих бактерий, чтобы решить, с какой я буду работать дальше. Еще я добавил к ним Photobacterium gaetbulicola, про геном которой писал мини-обзор (почему нет?). Результаты показаны на рис. 2. (использовал WebLogo3, базовые частоты букв считал одинаковыми).
Кстати, о лого: пока я их разглядывал, я понял, что объяснение, что значат высоты букв, данное в лекции — неправильное. Там оно звучит так: «высота буквы равна информационному содержанию этой буквы в предположении, что базовые частоты букв одинаковые; если информационное содержание отрицательное, то буква не изображается». В лекции говорится, что определение Шнайдера для расчета информационного содержания используется как основное, поэтому меня насторожило, что в большинстве колонок изображены все четыре буквы, потому что так не может быть: \[ \text{IC}_j(b) = f_j(b) \cdot \log_2 \frac{f_j(b)}{p(b)} \] Чтобы \(\text{IC}_j(b)\) было строго больше нуля для каждой буквы, \(f_j(b)\) должно быть строго больше \(p(b)\) для каждой буквы, а это, очевидно, невозможно, потому что и те, и другие должны давать в сумме единицу.
Информационное содержание по Шеннону всех букв может быть положительным, но почему строить лого таким методом, используя его — плохая идея, см. в приложении 1.
Пока я искал сервис, чтобы нарисовать лого, я нашел довольно много вариаций (см., напр., kplogo.wi.mit.edu), но такого определения, как в лекции, нигде не видел. Стандартное лого, в том числе на рис. 2, изображается так: высота всей колонки приравнивается к суммарному информационому содержанию этой колонки, а внутри колонки относительные высоты букв равны их частотам (Schneider, Stephens, 1990). Соответственно, в колонке всегда будут изображены четыре буквы, только если какие-то из них не отсутствовали в этой колонке или не были настолько редкими, что окажутся на визуализации тоньше пикселя.
Я прочитал статью, на которую Андрей Владимирович ссылался в лекции, про последовательность Козак у бактерий (Saito et al., 2020). В нескольких предложениях я пересказал бы ее так:
Во-первых, сила последовательности Шайна — Дальгарно (SD) у гена, измеренная как −ΔG образования дуплекса с 3'-концом 16S рРНК (ASD), все-таки коррелирует с тем, насколько мРНК оказывается занята рибосомами, вопреки результатам предыдущих работ.
Во-вторых, SD не нужна для определения верного старт-кодона. Для того, чтобы AUG служил местом инициации транскрипции, необходима не последовательность Шайна-Дальгарно, а A-богатая последовательность перед старт-кодоном (рис. 3). Видно, что после старт-кодона тоже есть A-богатый участок. Сами авторы не называют это последовательностью Козак, но проводят аналогию в обсуждении.
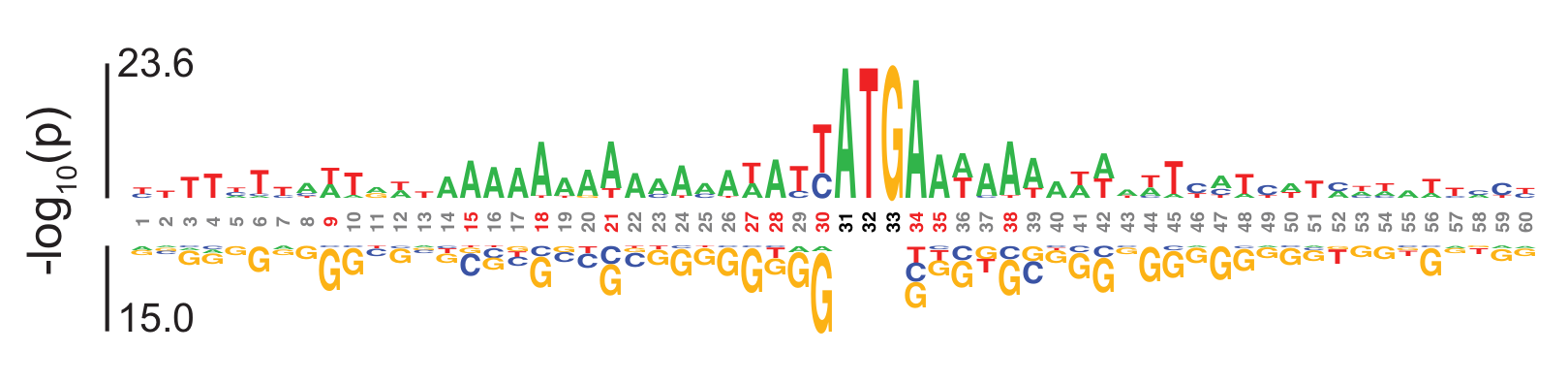
В общем, на лого, построенном для всех генов, тоже можно заметить обогащение A, особенно сразу после старт-кодона. (рис. 2., E. coli).
Кроме того, авторы приводят просто набор лого для нескольких бактерий, когда обсуждают полученные результаты (рис. 4). Мне показалось, что здесь он тоже будет уместен — интересно же сравнить!
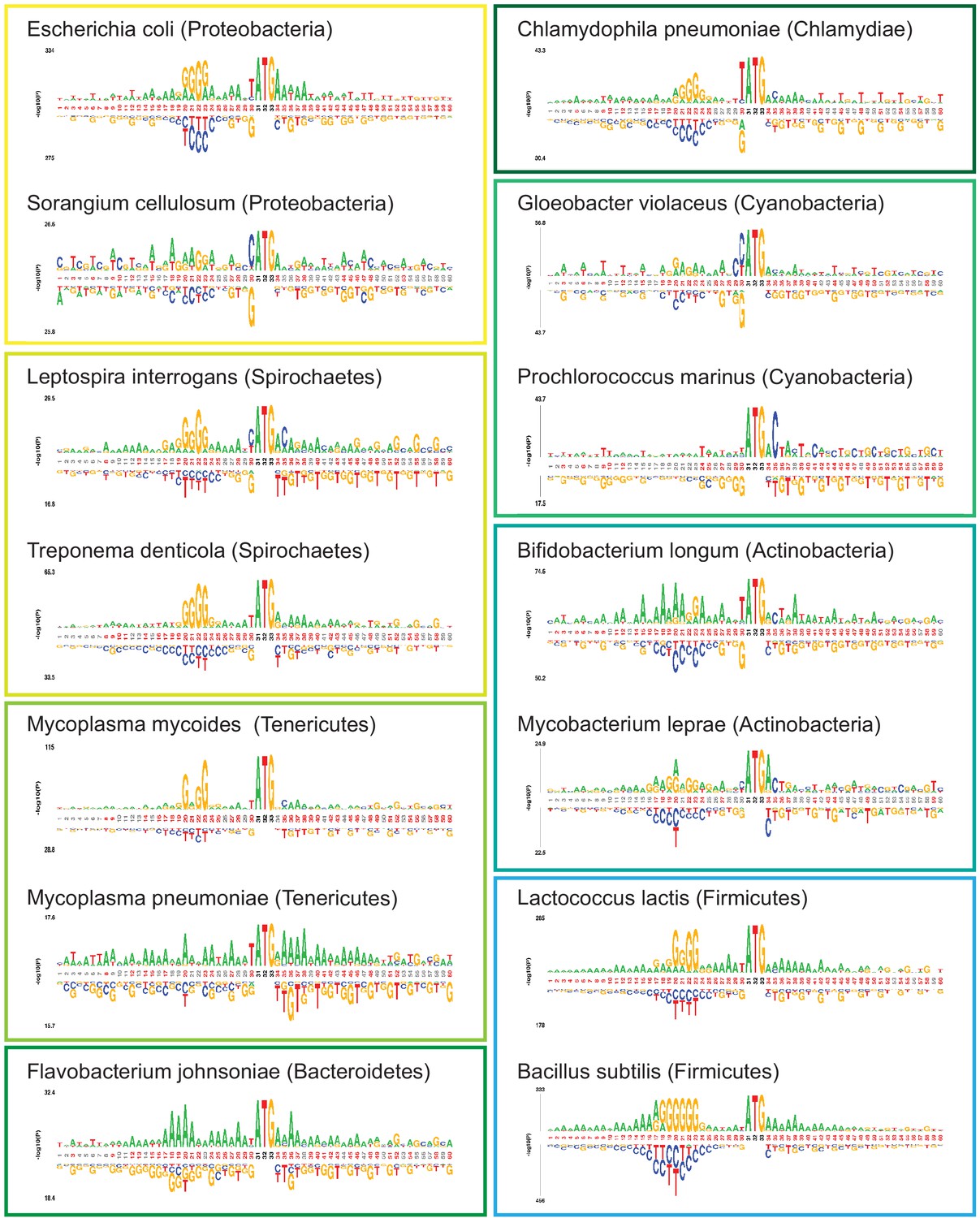
Ну, с E. coli авторы разобрались, и воспроизводить то же самое, только хуже, будет не очень интересно. Окрестности старт-кодона P. gaetbulicola оказались удивительно похожими на E. coli (рис. 2), особенно если сравнить с тем, насколько разными они могут быть внутри одного рода для Mycoplasma (рис. 4).
У M. pneumoniae видно некоторое обогащение A перед старт-кодоном и чуть более сильное после. Учитывая, что у нее всего 15% генов имеют SD (Srivastava et al., 2016) (на лого для всех генов SD вообще не видно), это очень хорошо согласуется с результатами обсуждаемой статьи. Посмотреть сюда подробнее могло бы быть интересно, но микоплазма все-таки меркнет в сравнении с Gracilibacteria — ее окрестности старт-кодона выглядят очень интересно и не похожи ни на что другое, и анализировать дальше я буду, конечно, ее.
Первая моя мысль, когда я это увидел, была про то, что у нее может быть просто другая ASD, а значит это может оказаться SD; но нет — ее ASD отличается, но не настолько, SD все равно должна состоять в основном из G (рис. 2).
Следующее замечание, которое можно сделать — в геноме Gracilibacteria низкое содержание GC, 28.8%. У E. coli и P. gaetbulicola оно почти равно 50%, поэтому для них предположение о равенстве базовых частот практически ничего не меняет, но для Gracilibacteria в AT-богатом участке перед старт кодоном на самом деле не так много информации, как кажется по рис. 2.
Потом я нашел библиотеку на Python, которая рисует лого по произвольной таблице с высотами букв (logomaker), поэтому я решил нарисовать его по определению из лекции, но учтя реальные базовые частоты букв, чтобы посмотреть, насколько эти участки на самом деле обогащены A и T. Кроме того, я взял еще чуть более широкую окрестность (рис. 5).
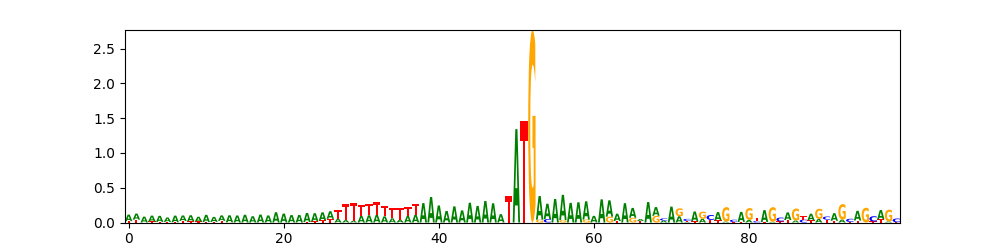
Видно, что, во-первых, действительно обогащены. Во-вторых, информационное содержание падает после ≈23 нуклеотидов upstream от старт-кодона, т.е. это будто бы дейтсвительно мотив, ассоциированный со старт-кодоном. В-третьих, видно, что после примерно четырех кодонов вглубь гена исчезает обогащение A и появляется другой очень милый паттерн: первая позиция кодонов обогащена G, третья — A.
Таким образом, я назначу участок −22...+12 «последовательностью Козак» и буду работать с ним.
Я случайно разделил CDS пополам (получилось по 598 — это train и test), нашел все ATG внутри CDS и выбрал из них столько же (это control). Я не брал ATG, которые лежали слишком близко к границе CDS, потому что мне было лень вытаскивать окружающие CDS последовательности. Так получились train, test и control. Построил по train PWM, посчитал веса для train, test и control, нарисовал гистограммы (рис. 6).
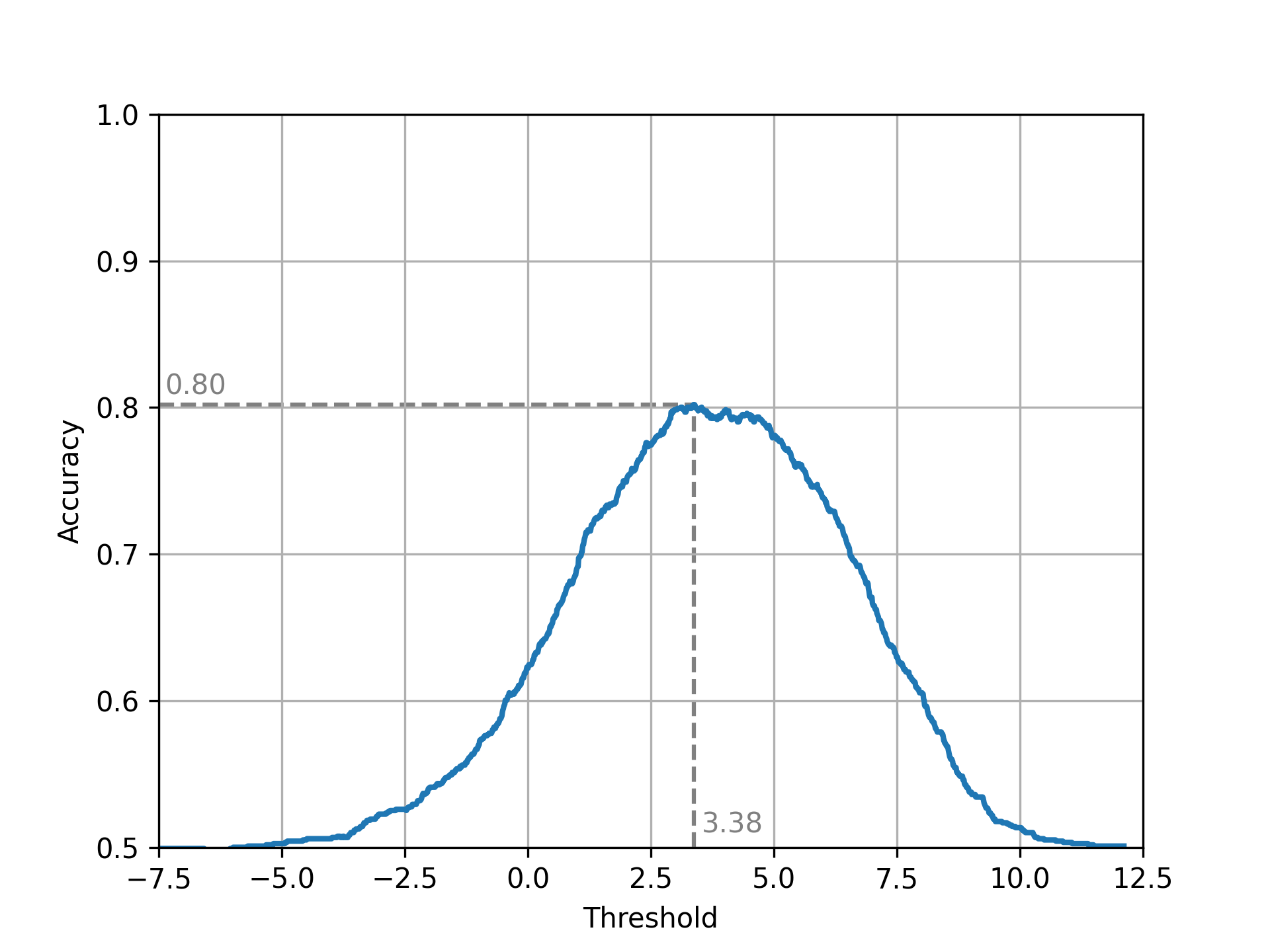
Теперь нужно выбрать порог. Выбирать буду так, чтобы итоговая табличка выглядела лучше всего, т.е. чтобы доля верно классифицированных последовательностей («accuracy») среди test и control была максимальной. Для этого построю зависимость accuracy от выбранного порога (рис. 7).
При значении порога в 3.38 балла 80.2% последовательностей из test и control оказываются классифицированы правильно (табл. 1).
| Motif | Train | Test | Control |
|---|---|---|---|
| + | 528 | 486 | 125 |
| − | 70 | 112 | 473 |
Информационное содержание мотива (по Шнайдеру) — 8.6 бит, и 5.4 из них приходится на старт-кодон. Не слишком много для такой длины.
«Выводы»
То, что 80% последовательностей из test и control удается верно классифицировать по этой PWM, намекает на то, что мотив, может быть, и правда существует. С другой стороны, может получится, например, так, что у этой бактерии кодирующие последовательности богаче GC, некодирующие богаче AT, единственная разница между этими выборками — это GC-состав, и, если бы мы брали контроль из некодирующих последовательностей, у нас бы ничего не вышло. GC-состав выборок действительно сильно различается: в train и test это 18.9 и 19.7% соответственно, а в control — 30.6%. Если все последовательности из test и control, в которых восемь или меньше букв GC, записывать как «+», а те, в которых девять или больше — как «−», мы получим accuracy в 78.1%, т.е. практически столько же, сколько с использованием PWM. (Может быть, если считать не GC против AT, а каждую букву по отдельности, и провести границу не в одномерном, а в трехмерном пространстве, то можно будет дискриминировать последовательности только по их составу значительно точнее, потому что, судя по виду мотива, сильнее всего он обогащен именно A, но вот это мне уже лень делать). В общем, следующая очевидная вещь, которую хочется сделать — взять контроль из некодирующих последовательностей и посмотреть, что получится.
Механизм, с помощью которого рибосома узнает A-богатые участки у нужных старт-кодонов РНК без последовательности Шайна — Дальгарно у E. coli, неизвестен (Saito et al., 2020). Вероятно, мотив, который мы нашли здесь, это то же самое и он нужен для инициации трансляции, но точно сказать, естественно, нельзя. Ни одной статьи по инициации трансляции у Gracilibacteria я не нашел.
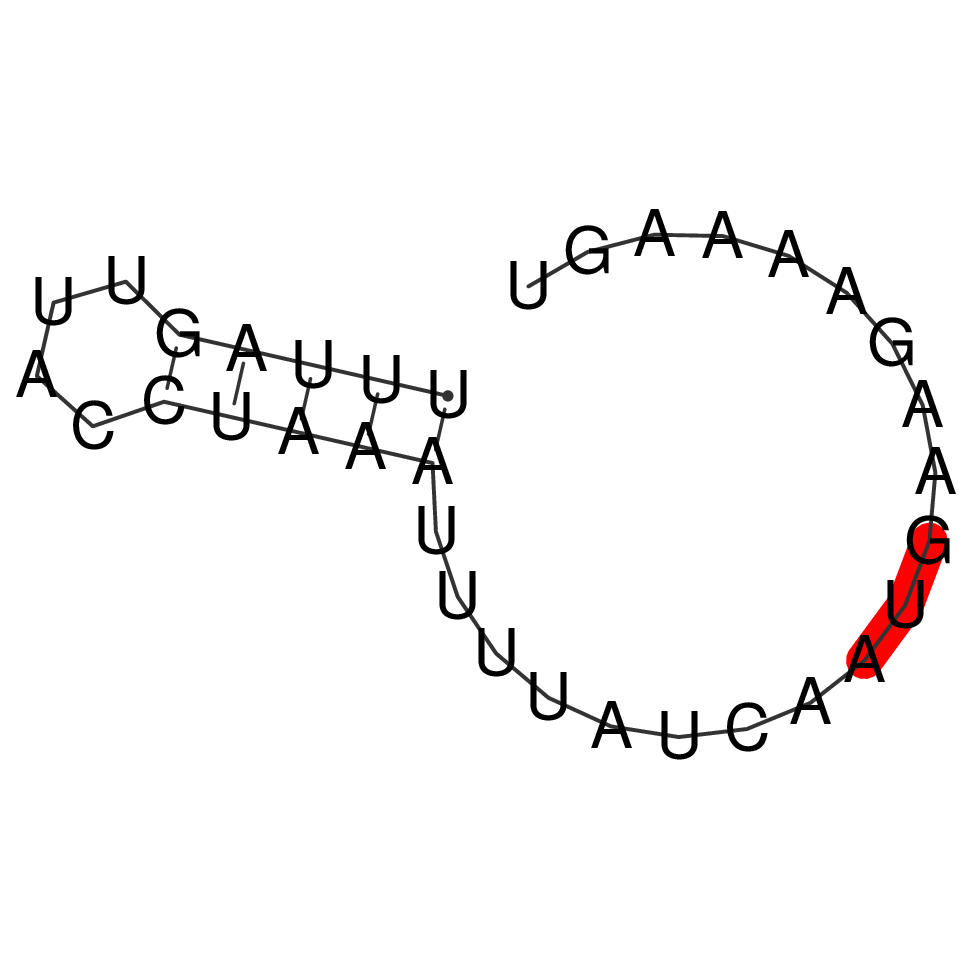
Вторая мысль, которая приходит в голову, когда смотришь на консенсус этого мотива — «да он же свернется в шпильку!» Чесслово, он ведь состоит из 11 T и 11 A подряд. Но мотив довольно слабый, и ни одной реальной последовательности, совпадающей с консенсусом, в геноме нет. Я подумал, что, может быть, они отличаются от консенсуса, но так, чтобы самокомплементарность сохранялась, и решил быстро это проверить. Взял три случайных последовательности и свернул их с помощью ViennaRNA. В двух вообще не было вторичной структуры, третья образовала шпильку, но короткую и близко к одному концу, а не так, как я ожидал (рис. 8). Ну, эта идея оказалась неправильной.
Материалы и методы
AC геномов есть в практикуме 13 первого семестра и в мини-обзоре.
Скрипт pr8.sh разбирает геном на нужные кусочки (окрестности старт-кодонов, целиковые CDS для контроля, 16S рРНК, чтобы посмотреть, какой должна быть SD). Скрипт pwm.py делает все остальное.
Чтобы нарисовать картинку свернутой РНК:
echo UUUAGUUACCUAAAUUUUAUCAAUGAAGAAAAGU | RNAfold > example_rna.fold
RNAplot --pre '23 25 8 RED omark' < example_rna.fold
Приложение 1
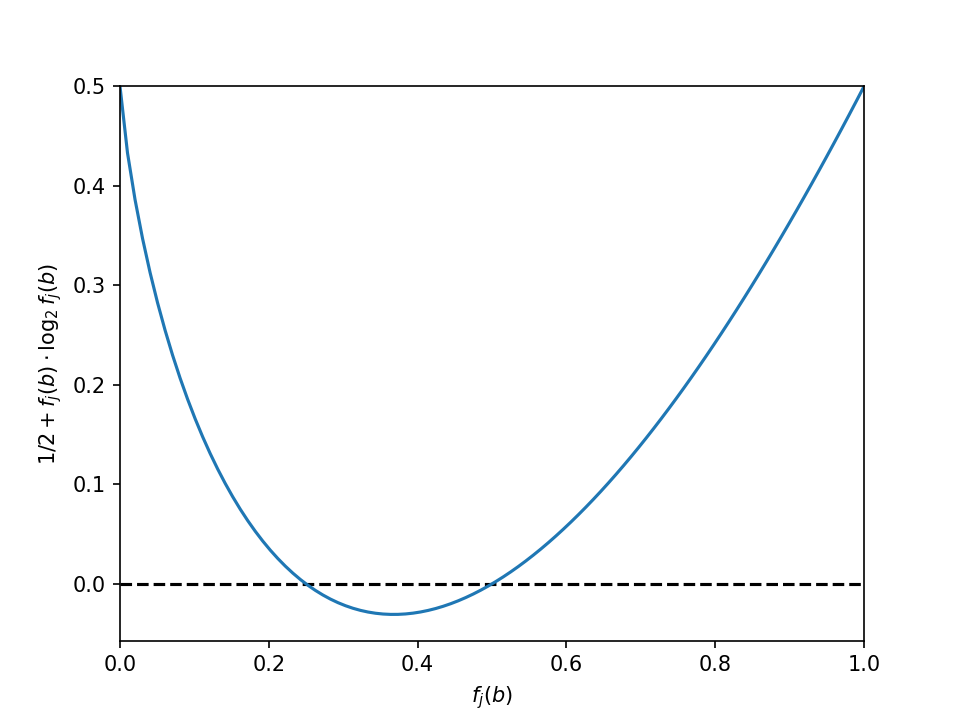
Информационное содержание колонки выравнивания по Шеннону определяется так: \begin{split} \text{IC}_j &= H_g - H_j \\ &= -\sum_b p(b) \log_2 p(b) + \sum_b f_j(b) \log_2 f_j(b) \end{split} Значит, \(\text{IC}_j(b)\) будет выглядеть как \[ -p(b) \log_2 p(b) + f_j(b) \log_2 f_j(b) \] , или, если базовые частоты букв равны, \[ \frac{1}{2} + f_j(b) \log_2 f_j(b) \] Если посмотреть на график этой функции, видно, что она немонотонна (рис. 8).
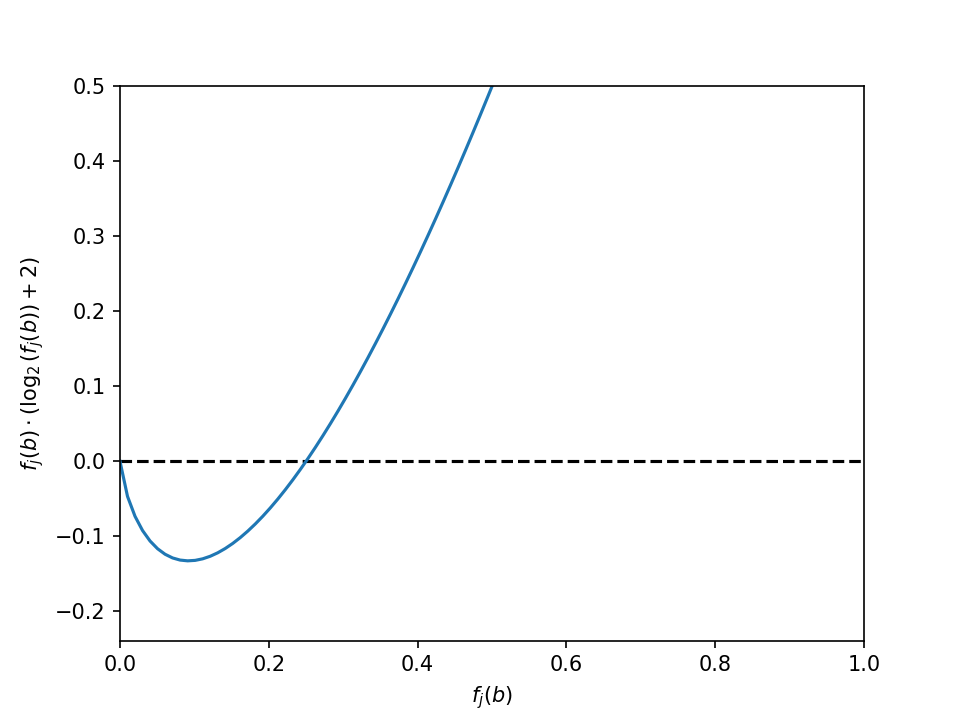
Ее нули — это 1/4 и 1/2 (можно проверить, подставив), поэтому на лого будут изображены, ну, «информативные» буквы: либо редкие, либо частые. Поэтому лого будет выглядеть совсем не так, как нам хочется. Например, если частоты букв равны 0.7, 0.1, 0.1, 0.1, то будут изображены все четыре буквы, но та, частота которой равна 0.7, будет ниже остальных: \(\text{IC}_j(b:\ f_j(b) = 0.7) = 0.140\), \(\text{IC}_j(b:\ f_j(b) = 0.1) = 0.168\). Или, например, если только одна буква редкая и имеет частотуИнформационное содержание по Шнайдеру монотонно там, где положительно (рис. 10), поэтому с ним рисовать лого по определению из лекции можно.
Список литературы
- Mendoza-Vargas, Alfredo, Leticia Olvera, Maricela Olvera, Ricardo Grande, Leticia Vega-Alvarado, Blanca Taboada, Verónica Jimenez-Jacinto, et al. 2009. “Genome-Wide Identification of Transcription Start Sites, Promoters and Transcription Factor Binding Sites in E. Coli.” PLOS ONE 4 (10): e7526. https://doi.org/10.1371/journal.pone.0007526.
- Saito, Kazuki, Rachel Green, and Allen R Buskirk. 2020. “Translational Initiation in E. Coli Occurs at the Correct Sites Genome-Wide in the Absence of mRNA-rRNA Base-Pairing.” Edited by Joseph T Wade, James L Manley, Joseph T Wade, and Alexander Mankin. eLife 9 (February):e55002. https://doi.org/10.7554/eLife.55002.
- Schneider, Thomas D., and R.Michael Stephens. 1990. “Sequence Logos: A New Way to Display Consensus Sequences.” Nucleic Acids Research 18 (20): 6097–6100. https://doi.org/10.1093/nar/18.20.6097.
- Srivastava, Ambuj, Prerana Gogoi, Bhagyashree Deka, Shrayanti Goswami, and Shankar Prasad Kanaujia. 2016. “In Silico Analysis of 5′-UTRs Highlights the Prevalence of Shine–Dalgarno and Leaderless-Dependent Mechanisms of Translation Initiation in Bacteria and Archaea, Respectively.” Journal of Theoretical Biology 402 (August):54–61. https://doi.org/10.1016/j.jtbi.2016.05.005.