Исследуйте качество восстановления функции ЭП от одной переменной в зависимости от того, какие и сколько гармоник ряда Фурье используются для ее восстановления.Функцию задали с помощью предосталенного скрипта compile-func.py с параметрами: 10,3,8+7,4,9+20,1.5,15+20,1.5,20+15,1,17. Одновремено с ниже представленным рисунком был создан файл. Рис.1 График заданной функции ЭП Далее с помощью программы func2fourier.py были найдены коэффициенты Фурье. Выходной файл func_ft.txt содержит амплитуды и фазы гармоник с соответствующими номерами. Получилось 498 гармоник. После с помощью скрипта fourier-filter.py были отобраны некоторые гармоники, количество гармоник менялось и с помощью скрипта проводилось востановление. Все данные будут представлены в таблице№1 и рисунках. Уже при разрешение 1-1.2A функция востанавливается очень хорошо. 
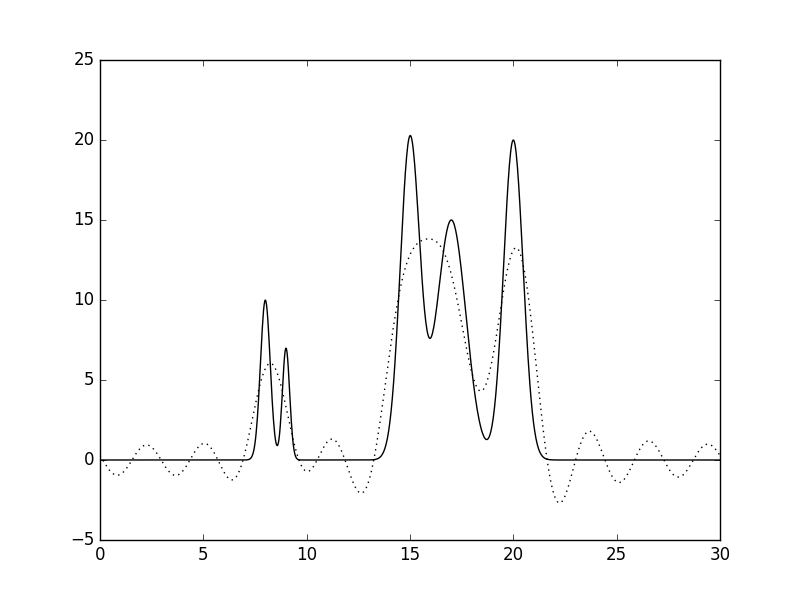 Рис.2 Восстановленная по полному набору гармоник функция ЭП (n=10, d=3A). 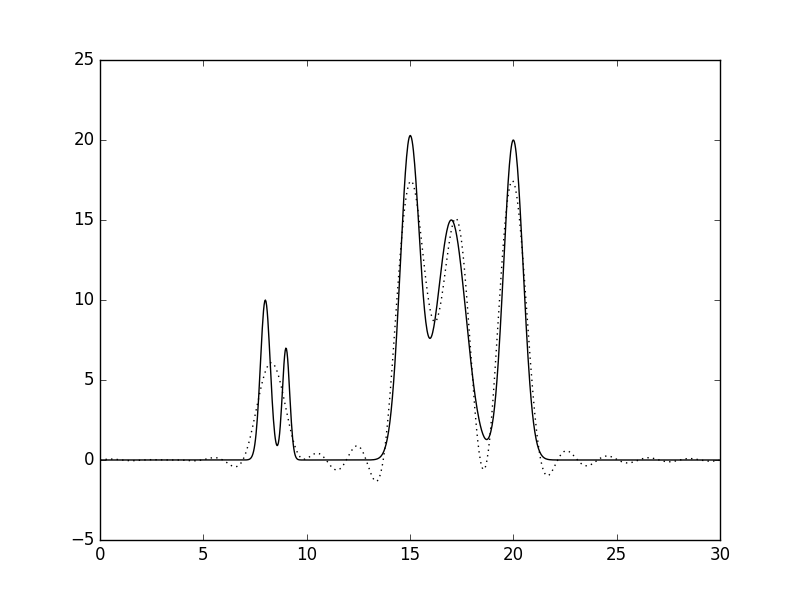 Рис.3 Восстановленная по полному набору гармоник функция ЭП (n=15, d=2A). 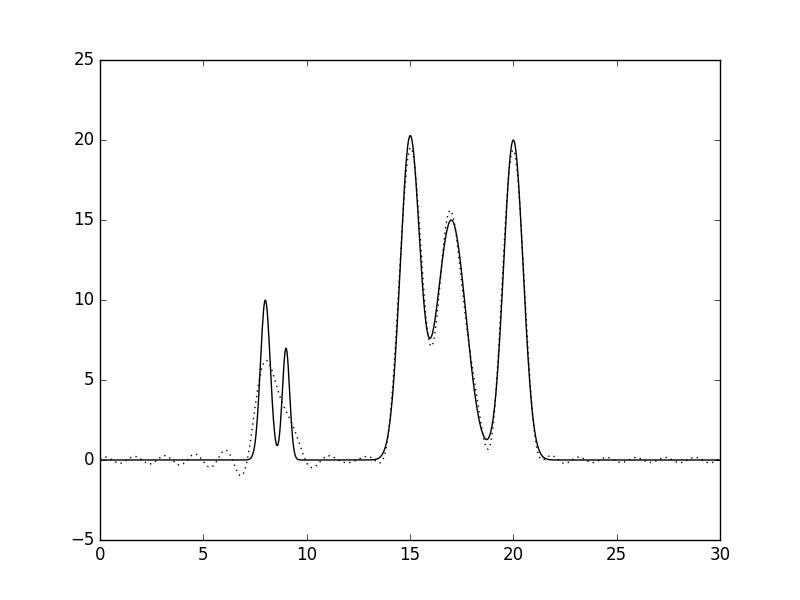 Рис.4 Восстановленная по полному набору гармоник функция ЭП (n=20, d=1.5A). 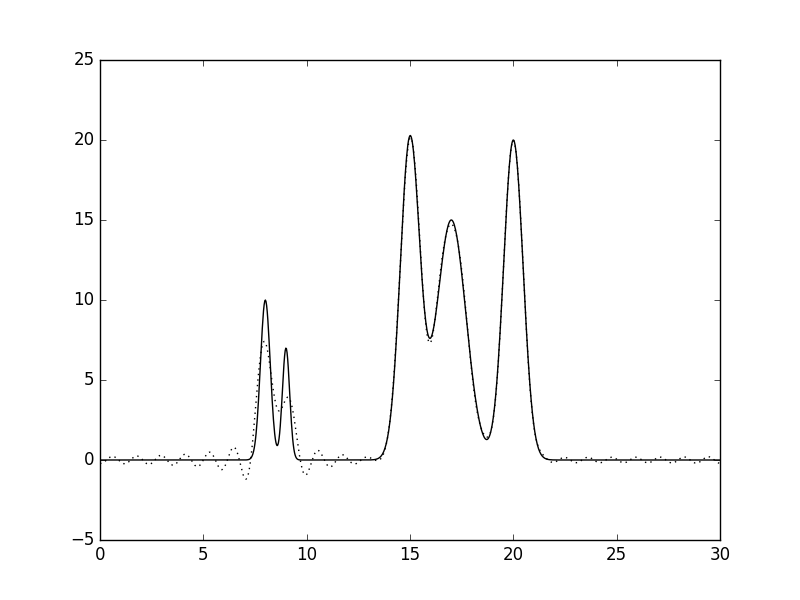 Рис.5 Восстановленная по полному набору гармоник функция ЭП (n=25, d=1.2A). 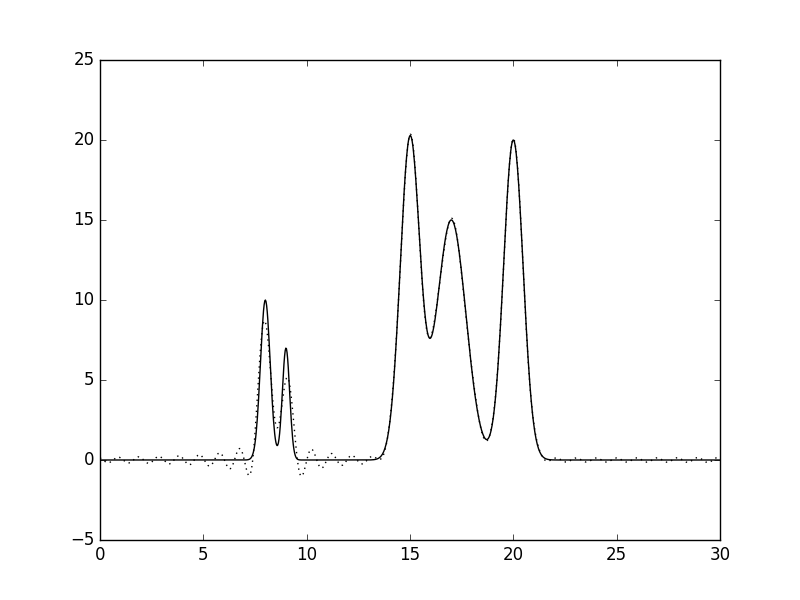 Рис.6 Восстановленная по полному набору гармоник функция ЭП (n=30, d=1A). 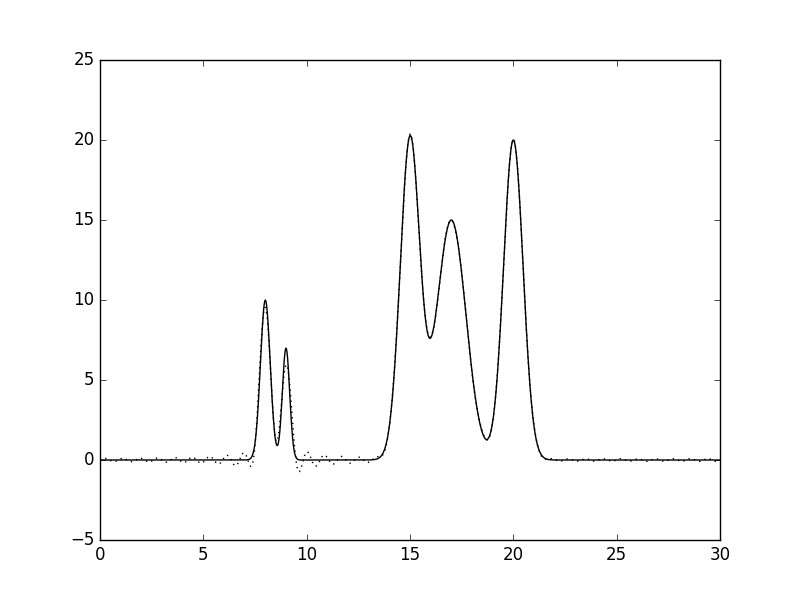 Рис.7 Восстановленная по полному набору гармоник функция ЭП (n=35, d=0.85A). Далее будем использовать только 35 гармоник и будем добавлять разные шумы в эксперемент (F (включение случайного и "нормально распределённого" шума в значения амплитуд) и -P (аналогично для фаз гармоник). Все данные будут представлены в таблице№1 и рисунках. 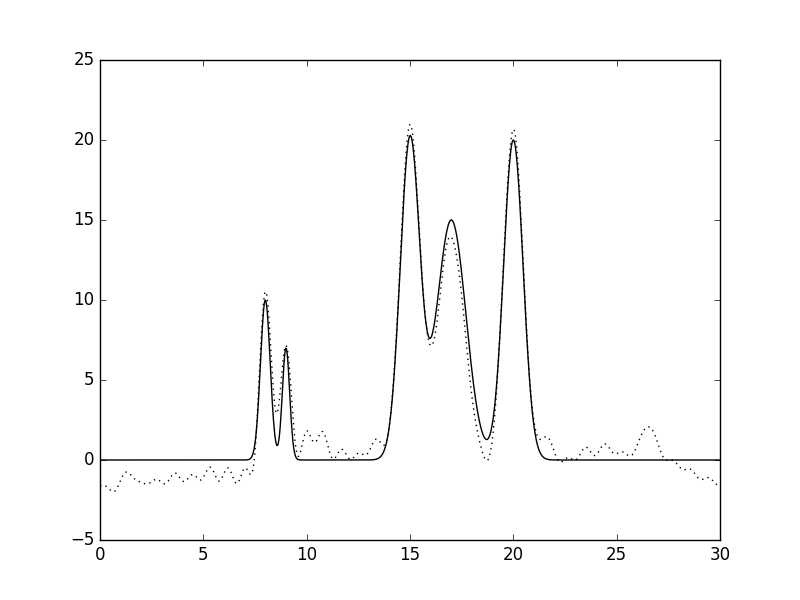 Рис.8 Восстановленная по полному набору гармоник функция ЭП c шумом (n=35, d=0.85A F=20 P=0). 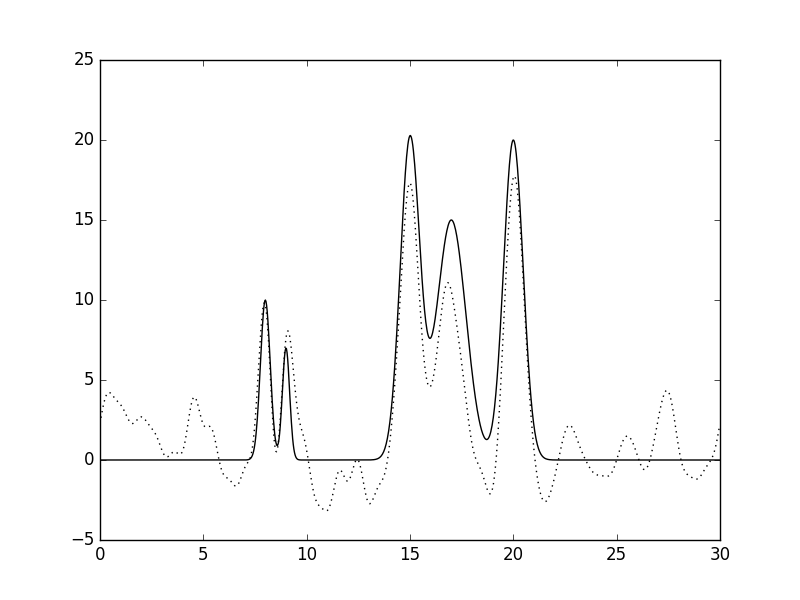 Рис.9 Восстановленная по полному набору гармоник функция ЭП с шумом (n=35, d=0.85A F=40 P=0). 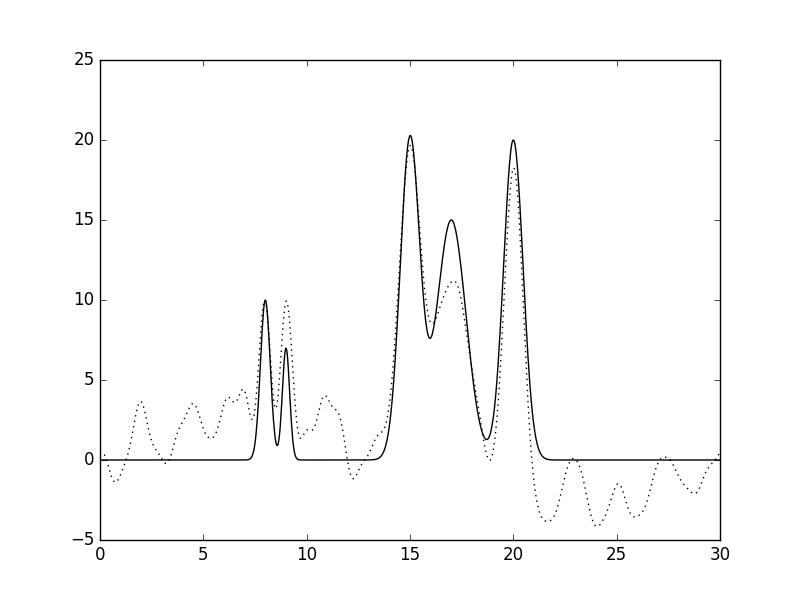 Рис.10 Восстановленная по полному набору гармоник функция ЭП с шумом (n=35, d=0.85A F=0 P=20). 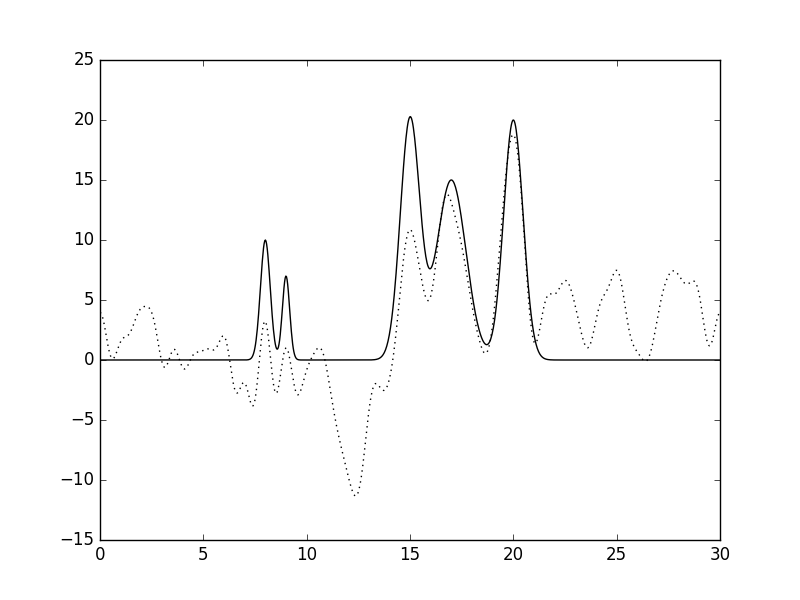 Рис.11 Восстановленная по полному набору гармоник функция ЭП с шумом (n=35, d=0.85A F=0 P=40). 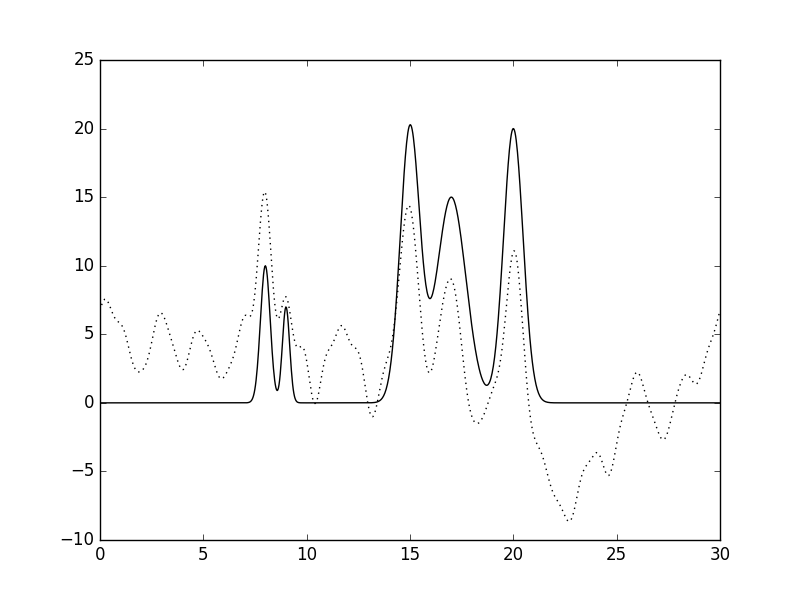 Рис.12 Восстановленная по полному набору гармоник функция ЭП с шумом (n=35, d=0.85A F=20 P=40). 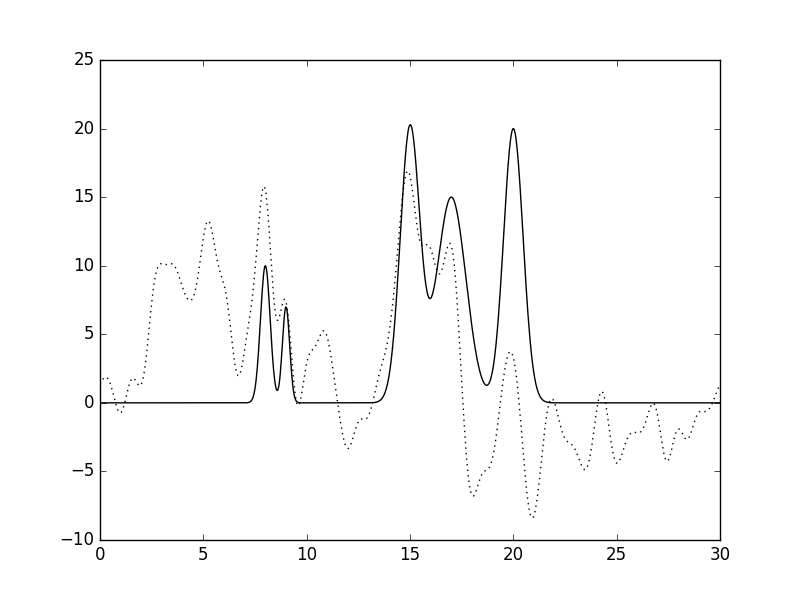 Рис.13 Восстановленная по полному набору гармоник функция ЭП с шумом (n=35, d=0.85A F=40 P=40). 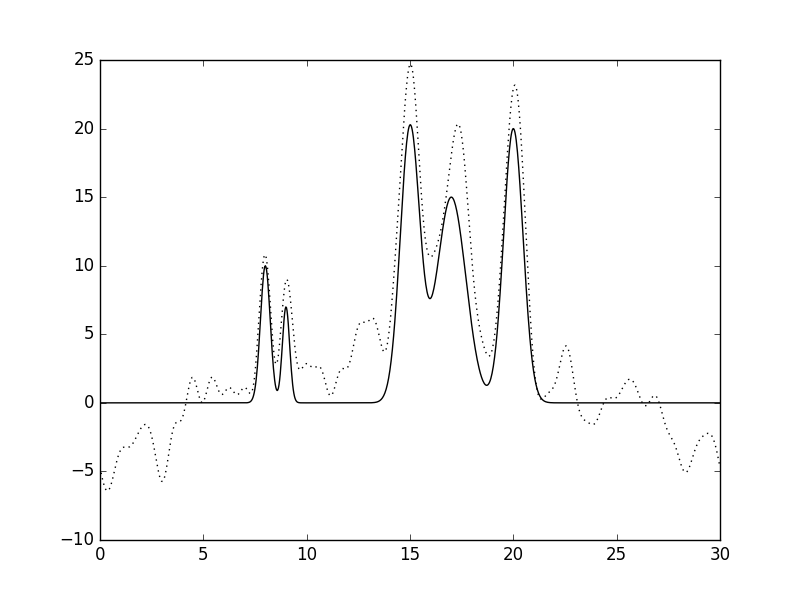 Рис.14 Восстановленная по полному набору гармоник функция ЭП с шумом (n=35, d=0.85A F=40 P=20). 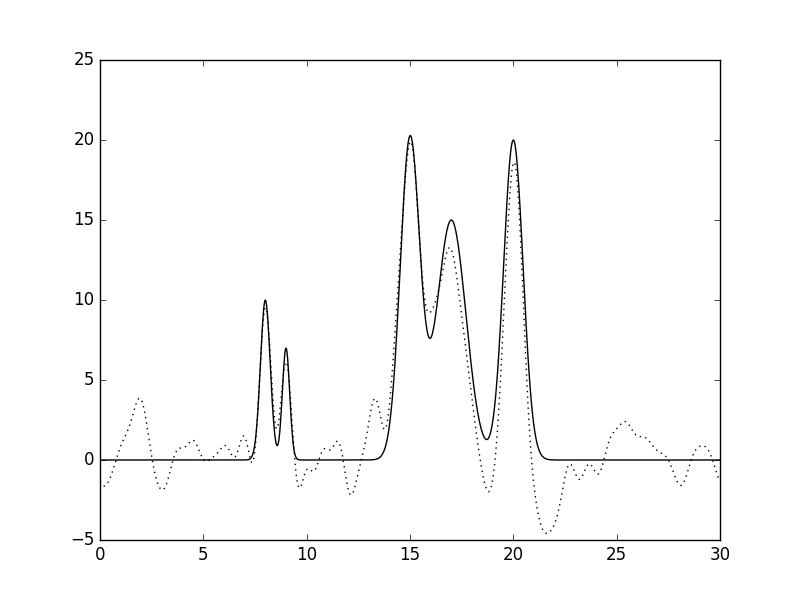 Рис.15 Восстановленная по полному набору гармоник функция ЭП с шумом (n=35, d=0.85A F=20 P=20). Теперь будем использовать неполный набор гармоник. Сначала уберем основопологающею первую гармнонику(Рис.16). Если убрать последние 10 гармоник, то не происходит сильного изменения. 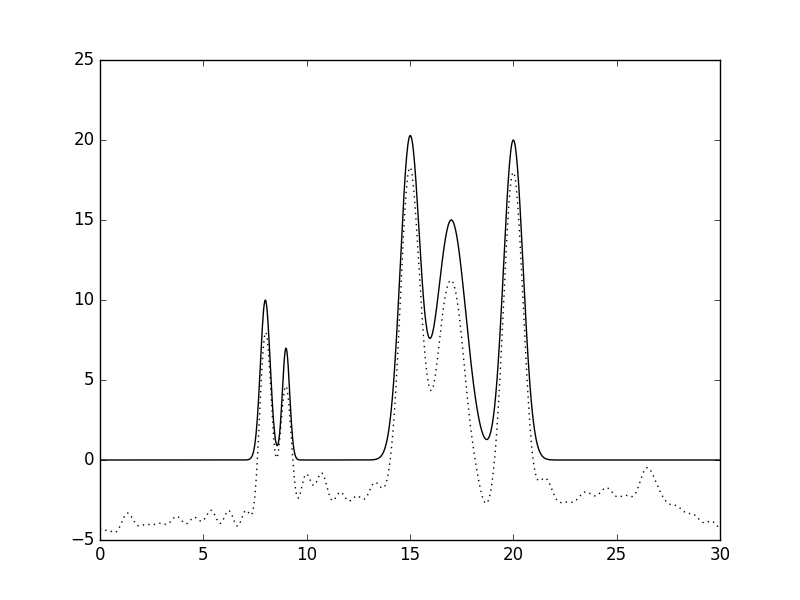 Рис.16 Восстановленная по неполному набору гармоник функция ЭП с шумом (n=35, d=0.85A F=0 P=0). |