Занятие 1: Общие представления о филогенетических деревьях.
Занятие 1
Отобранные бактерии
| Название | Мнемоника |
| Clostridium botulinum | CLOB1 |
| Lactobacillus acidophilus | LACAC |
| Lactococcus lactis | LACLM |
| Streptococcus pneumoniae | STRPN |
| Bacillus anthracis | BACAN |
| Bacillus subtilis | BACSU |
| Listeria monocytogenes | LISMO |
| Staphylococcus epidermidis | STAES |
Скобочная формула дерева
(CLOB1,((LACAC,(LACLM,STRPN)),((LISMO,(BACAN,BACSU)),STAES)));
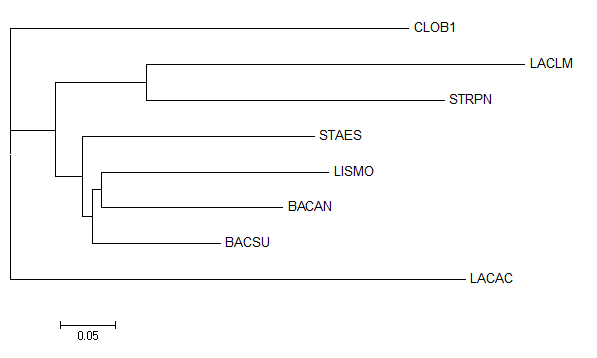
Изображение дерева
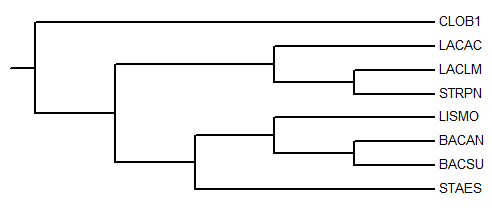
Ветви дерева
Дерево содержит пять нетривиальных ветвей:
1){LACLM,STRPN} против {CLOB1,LACAC,LISMO,BACAN,BACSU,STAES}
2){LACAC,LACLM,STRPN} против {CLOB1,LISMO,BACAN,BACSU,STAES}
3){BACAN,BACSU} против {CLOB1,LACAC,LACLM,STRPN,LISMO,STAES}
4){LISMO,BACAN,BACSU} против {CLOB1,LACAC,LACLM,STRPN,STAES}
5){LISMO,BACAN,BACSU,STAES} против {CLOB1,LACAC,LACLM,STRPN}
Занятие 2
Упражнение 1
Пользуясь таксономическим сервисом NCBI: http://www.ncbi.nlm.nih.gov/taxonomy/, я определила, к каким таксонам относятся отобранные мною на предыдущем занятии бактерии.
Таксономия:
Clostridium botulinum : Bacteria; Firmicutes; Clostridia; Clostridiales; Clostridiaceae; Clostridium
Lactobacillus acidophilus : Bacteria; Firmicutes; Bacilli; Lactobacillales; Lactobacillaceae; Lactobacillus
Lactococcus lactis : Bacteria; Firmicutes; Bacilli; Lactobacillales; Streptococcaceae; Lactococcus
Streptococcus pneumoniae : Bacteria; Firmicutes; Bacilli; Lactobacillales; Streptococcaceae; Streptococcus
Bacillus anthracis : Bacteria; Firmicutes; Bacilli; Bacillales; Bacillaceae; Bacillus; Bacillus cereus group
Bacillus subtilis : Bacteria; Firmicutes; Bacilli; Bacillales; Bacillaceae; Bacillus; Bacillus subtilis group
Listeria monocytogenes : Bacteria; Firmicutes; Bacilli; Bacillales; Listeriaceae; Listeria
Staphylococcus epidermidis : Bacteria; Firmicutes; Bacilli; Bacillales; Staphylococcaceae; Staphylococcus
Ветви, выделяющие какие-либо из таксонов, отобржены на рисунке:
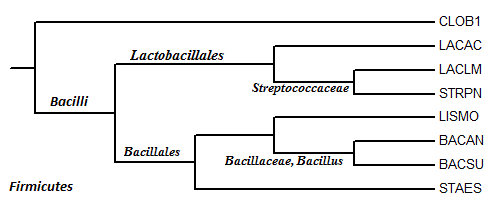
Упражнения 2 и 3
Для реконструкции филогенетического дерева был выбран фактор инициации трансляции 2 (мнемоника IF2)
Получила из Swiss-Prot последовательности белков с данной функцией из отобранных мною бактерий. Выровняла последовательности программой muscle.
Упражнение 4* - дополнительное

Диагностические позиции:
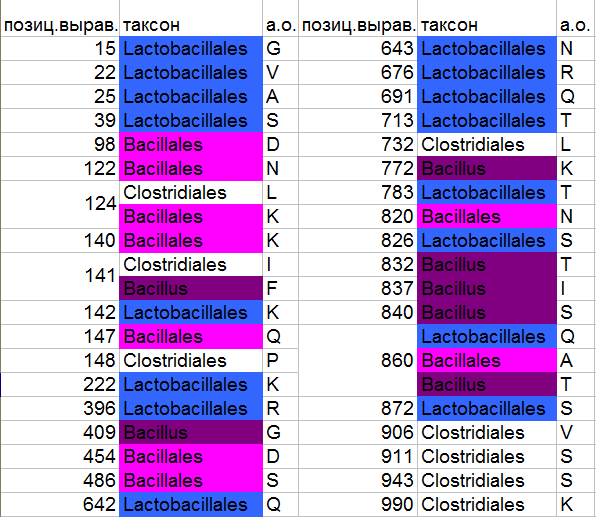
Упражнение 5: реконструкция филогенетического дерева программой fprotpars
Команда для запуска программы:
fprotpars -sequence if2_aligned.fasta -outfile if2_trees.fprotpars
Программа нашла всего одно дерево (неукорененное):
+--STRPN
+--------------3
! +--LACLM
+--2
! ! +-----------LISMO
! ! !
! +-----5 +--------STAES
! ! !
1 +--4 +--BACSU
! ! +--7
! +--6 +--BACAN
! !
! +-----CLOB1
!
+--------------------LACAC
Скобочная формула:
(LACAC, ((STRPN, LACLM), (LISMO, (STAES, (CLOB1, (BACSU, BACAN))))))
В полученном дереве и в правильном совпадают лишь две ветви (нетривиальные): {LACAC,LACLM,STRPN} vs {CLOB1,LISMO,BACAN,BACSU,STAES}
{BACAN,BACSU} vs {CLOB1,LACAC,LACLM,STRPN,LISMO,STAES}
, все остальные не соответствуют ветвям правильного дерева.
Упражнение 6: Оценка эволюционных расстояний между последовательностями программой fprotdist.
Матрица расстояний:
LACAC CLOB1 LACLM STRPN STAES LISMO BACAN BACSU
LACAC 0.000000 0.787550 0.883118 0.818371 0.701794 0.732684 0.678139 0.593545
CLOB1 0.787550 0.000000 0.857738 0.765318 0.616843 0.688236 0.600605 0.579657
LACLM 0.883118 0.857738 0.000000 0.624227 0.698932 0.655551 0.649035 0.582115
STRPN 0.818371 0.765318 0.624227 0.000000 0.605911 0.606991 0.571132 0.515740
STAES 0.701794 0.616843 0.698932 0.605911 0.000000 0.430918 0.411412 0.343205
LISMO 0.732684 0.688236 0.655551 0.606991 0.430918 0.000000 0.378702 0.342432
BACAN 0.678139 0.600605 0.649035 0.571132 0.411412 0.378702 0.000000 0.288485
BACSU 0.593545 0.579657 0.582115 0.515740 0.343205 0.342432 0.288485 0.000000
Утверждение ультраметричности гласит: "из трех расстояний между тремя объектами два всегда равны между собой и не меньше третьего"
Возьмем три последовательности: LACAC, STAES, BACSU
d(LACAC, STAES) = 0.701794
d(STAES, BACSU) = 0.343205
d(LACAC, BACSU) = 0.593545
Очевидно, что для данного случая аксиома ультраметричности не выполняется, т.к. даже в большом приближении нельзя найти равные расстояния.
Возьмем три других последовательности, например, из STAES, STRPN и LISMO:
d(STAES, STRPN) = 0.605911
d(STAES, LISMO) = 0.430918
d(STRPN, LISMO) = 0.606991
Первое и третье значения практически равны и больше второго, значит данная тройка удовлетворяет аксиоме ультраметричности.
Принцип аддитивности: если есть 4 последовательности: a, b, c, d, - то из трех сумм d(a,b) + d(c,d); d(a,c) + d(b,d); d(a,d) + d(b,c) две равны между собой и больше третьей.
Рассмотрим BACAN, LACLM, BACSU и CLOB1
d(BACAN,LACLM) + d(BACSU,CLOB1) = 0.649035 + 0.579657 = 1.228692
d(BACAN,BACSU) + d(LACLM,CLOB1) = 0.288485 + 0.857738 = 1.146223
d(BACAN,CLOB1) + d(LACLM,BACSU) = 0.600605 + 0.582115 = 1.182720
Эти последовательности, в принципе, могут удовлетворять принципу аддитивности, если принять, что значения первой и третьей сумм приблизительно равны. И они больше значения второй суммы.
Упражнение 7: Реконструкции дерева, полученные в программе fneighbor.
Команды для программы fneighbor:
fneighbor -datafile if2_matrix.fprotdist -outfile if2_nj.fneighbor -treetype n -outtreefile fn_tree_nj.fneighbor
fneighbor -datafile if2_matrix.fprotdist -outfile if2_upgma.fneighbor -treetype u -outtreefile fn_tree_upgma.fneighbor
Изображения построены в MEGA по полученным фйлам со скобочными формулами:
алгоритм UPGMA:
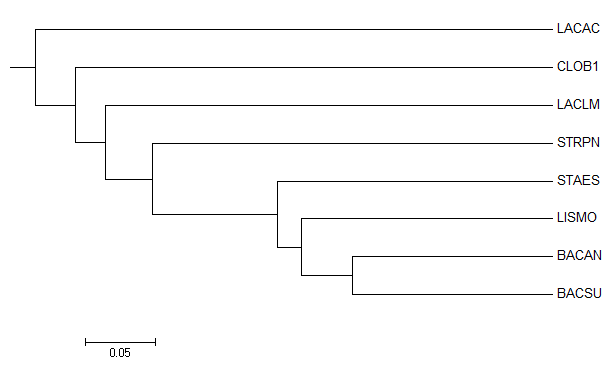
С правильным деревом совпадает ветвь (STAES,(LISMO,(BACAN,BACSU))) vs (CLOB1,LACAC,LACLM,STRPN), все остальное - неправильно. Это, по-видимому, означает, что дерево не подчиняется гипотезе молекулярны часов.
алгоритм Neighbor-Joining:
Я укоренила дерево в том же месте, где укоренено правильное: на ветви, отделяющей CLOB1 от всех остальных последовательностей. И затем проанализировала уже укорененное дерево. С правильным деревом совпадают ветви
(STAES,LISMO,BACAN,BACSU) vs (CLOB1,LACAC,LACLM,STRPN) и
(LISMO,BACAN,BACSU) vs (STAES,CLOB1,LACAC,LACLM,STRPN),
все остальное - неправильно. Причем данный алгоритм почему-то посчитал, что BACAN ближе к LISMO, чем к BACSU, хотя в действительности как раз наоборот.
Если же сравнивать между собой два дерева, полученные с помощью разных алгоритмов в программе fneighbor, то можно заметить, что в них совпадают ветви
(LISMO,BACAN,BACSU) vs (STAES,CLOB1,LACAC,LACLM,STRPN),
(STAES,LISMO,BACAN,BACSU) vs (CLOB1,LACAC,LACLM,STRPN),
(LACLM,STRPN,STAES,LISMO,BACAN,BACSU) vs (CLOB1,LACAC)
Упражнение 8* - дополнительное.
Для ознакомления с созданным в НИИФХБ имени А.Н. Белозерского сервисом TreeTop я ввела в поле Alignment свое выравнивание. Результат меня приятно поразил: все, что в предыдущих заданиях я получала с помощью различных программ, не имеющих удобного графического интерфейса, а именно: дерево в разных представлениях, матрицу расстояний, скобочные формулы - все это TreeTop выдал мне за пару секунд на одной сранице!
И для этого мне не пришлось набирать команды в командной строке с кучей параметров, названий входных и выходных файлов - я просто ввела выравнивание!
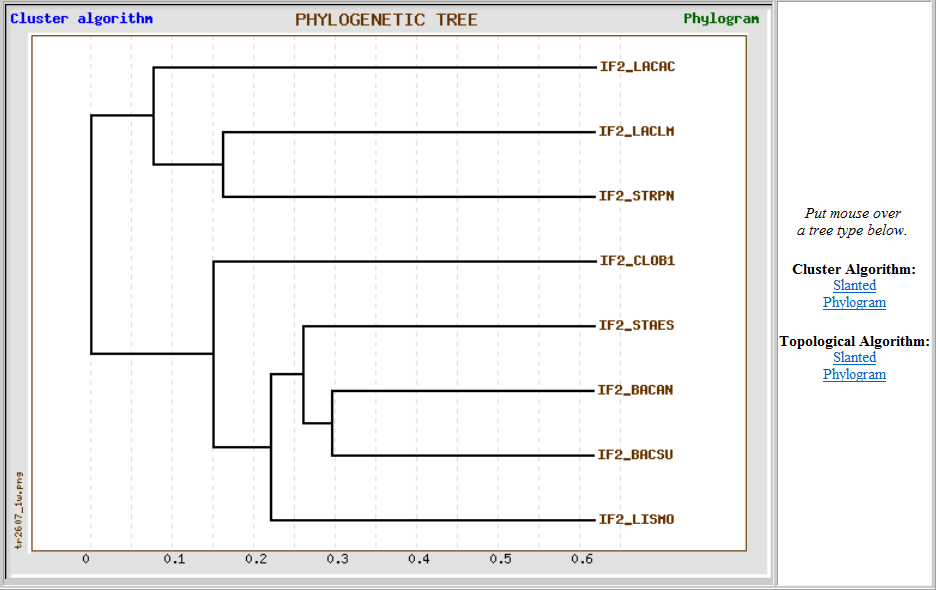
Дерево, полученное с помощью кластерного алгоритма, практически совпало с правильным (поменялись местами LISMO и STAES). И, кстати, если поводить мышкой по области справа от дерева, можно получить его еще и в угловой форме:
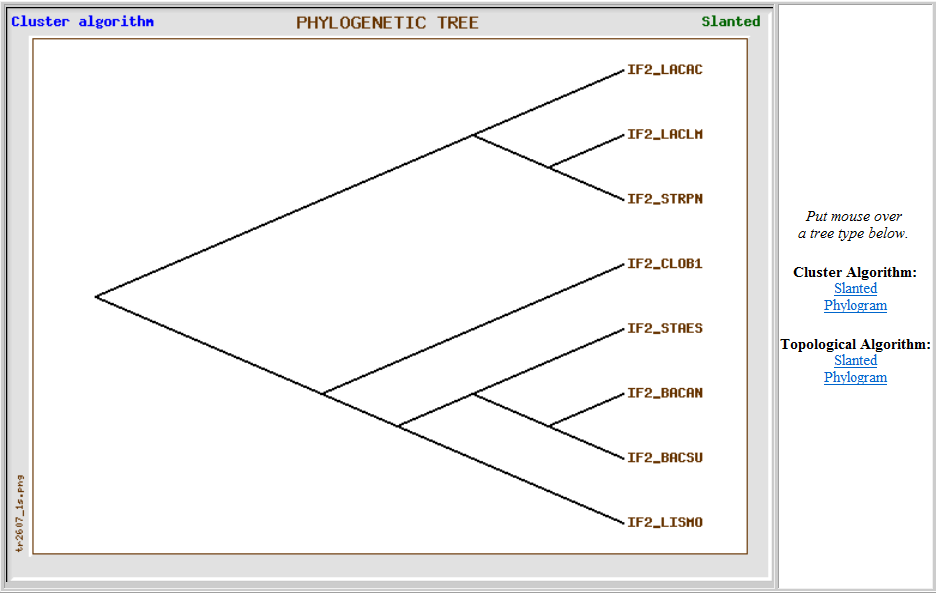
Дерево, полученное с помощью топологического алгоритма, имеет меньшее сходство с правильным:
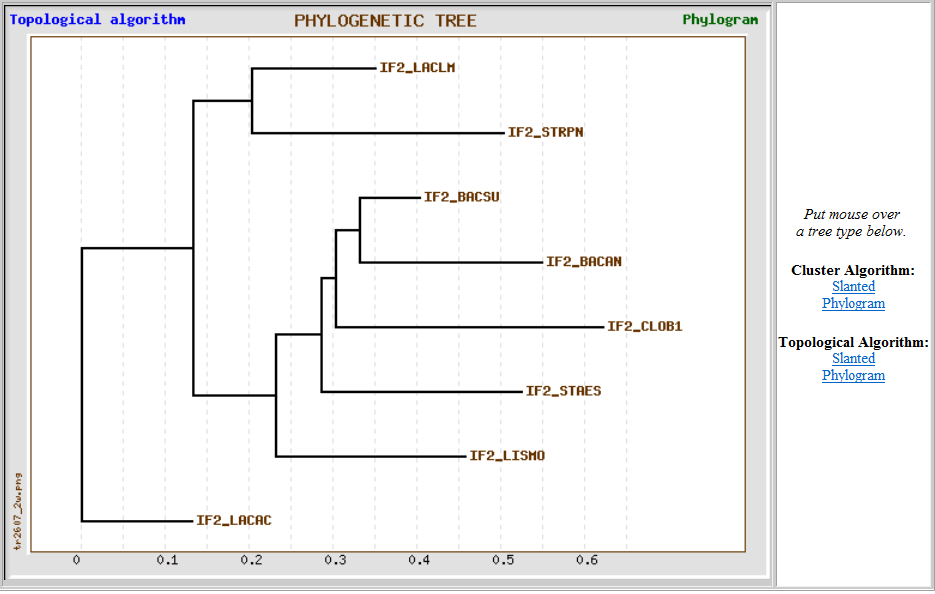
В целом мне очень понравился сервис, созданный в нашем НИИФХБ имени А.Н. Белозерского: удобный способ подачи входных данных и выдачи результатов, а интерфейс достаточно лаконичный и ненавязчивый, и разобраться новичку в нем несложно =)
E-mail: yan1303@yandex.ru
Официальный сайт ФББ
Ваши предложения :)))
Проекты
Главная страница