Анализ результатов моделирования самосборки липидного бислоя
Чтобы визуализировать результаты моделирования, воспользуемся командой trjconv -f b_md.xtc -s b_md.tpr -o b_pbc_1.pdb -skip 20. При вопросе о выводе групп выбираем DPPC.

Теперь попробуем команду trjconv -f b_md.xtc -s b_md.tpr -o b_pbc_2.pdb -skip 20 -pbc mol. Выводим группы - DPPC.
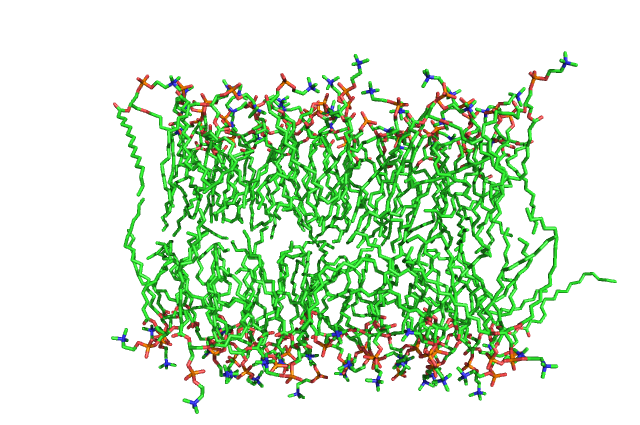
Трудно определить, на какой модели появляется четкий бислой. Чтобы понять это более точно, сделаем структуру с молекулами воды (нужно повторить предыдущую команду, а при вопросе о выводе групп выбрать System). Момент образования бислоя будем определять по исчезновению молекул воды из срединной гидрофобной части бислоя. В моем случае, это произошло при переходе от 23 модели к 24.
В файле .pdb рядом с записью MODEL 24 содержится информация о времени (в пикосекундах), когда образовался бислой:
TITLE bilayer in water t= 11500.00000
 |
 |
| Рис. 3a. Модель 23: слева видны молекулы воды в гидрофобном слое. | Рис. 3b. Модель 24: в гидрофобной части нет молекул воды. |
Определим зависимость площади, приходящейся на один липид, по осям Y и Z (X - нормаль к поверхности бислоя) от времени.
time1 = []
square = []
with open("box_1.xvg", 'r') as f1:
lines = f1.readlines()
for line in lines:
if (not line.startswith("@")) and (not line.startswith("#")):
linelist = line.split("\t")
time1.append(linelist[1])
square.append(float(linelist[3])*float(linelist[4])/32)
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
plt.plot(time1, square, c='purple',alpha=1)
plt.xlim()
plt.show()
При образовании бислоя липиды уплотняются и структурируются, поэтому и площадь, занимаемая одним липидом, уменьшается.
Построим зависимость изменения гидрофобной и гидрофильной поверхностей, доступных растворителю, от времени.
time2 = []
hphob = []
hphyl = []
with open("sas_b.xvg", 'r') as f2:
lines = f2.readlines()
for line in lines:
if (not line.startswith("@")) and (not line.startswith("#")):
linelist = line.split()
time2.append(linelist[0])
hphob.append(linelist[1])
hphyl.append(linelist[2])
plt.figure(figsize=(10,6))
plt.plot(time2, hphob, c='purple',alpha=1)
plt.plot(time2, hphyl, c='red',alpha=1)
plt.xlim()
plt.legend(['y = hydrophobic SAS', 'y = hydrophilic SAS'], loc='upper right')
plt.show()
В начале моделирования липиды расположены рыхло, и потому весь липид доступен для воды, при этом гидрофобная поверхность максимальна. Но это состояние не выгодно в присутствии растворителя, и гидрофобная поверхность резко снижается - сначала образуется мицеллоподобная структура. Далее на всем протяжении гидрофильная поверхность будет больше, чем гидрофобная, как ей и хочется. Дальнейшее слабое уменьшение поверхностей происходит из-за того, что липиды структурируются в бислой - они располагаются плотнее, поэтому поверхность, доступная растворителю становится меньше. Примерно на 15000 пс кривые выходят на условное плато - это время образования бислоя.

Оценим меру порядка в углеводородных хвостах липидов в начале и конце траектории. Задача осложняется тем, что в файле выдачи не указано, в каком из трех столбцов нужный коэффициент.
num = []
start1 = []
start2 = []
start3 = []
with open("ord_start.xvg", 'r') as f3:
lines = f3.readlines()
for line in lines:
if (not line.startswith("@")) and (not line.startswith("#")):
linelist = line.split()
num.append(linelist[0])
start1.append(linelist[1])
start2.append(linelist[2])
start3.append(linelist[3])
end1 = []
end2 = []
end3 = []
with open("ord_end.xvg", 'r') as f4:
lines = f4.readlines()
for line in lines:
if (not line.startswith("@")) and (not line.startswith("#")):
linelist = line.split()
end1.append(linelist[1])
end2.append(linelist[2])
end3.append(linelist[3])
plt.figure(figsize=(16,6))
plt.subplot(131)
plt.plot(num, start1, c='green',alpha=1)
plt.plot(num, end1, c='blue',alpha=1)
plt.legend(['y = start order', 'y = end order'], loc='upper left')
plt.subplot(132)
plt.plot(num, start2, c='green',alpha=1)
plt.plot(num, end2, c='blue',alpha=1)
plt.legend(['y = start order', 'y = end order'], loc='upper left')
plt.subplot(133)
plt.plot(num, start3, c='green',alpha=1)
plt.plot(num, end3, c='blue',alpha=1)
plt.legend(['y = start order', 'y = end order'], loc='upper right')
plt.show()
Судя по статье, эта мера порядка имеет значения от -1/2 (неупорядочено) до 1 (упорядочено). Это логически соотносится с крайним правым рисунком: вдоль каждой кривой упорядоченность падает с приближением к концу углеводородного хвоста (это логично, он более подвижен), а в конце траектории значения в целом выше, чем в начале, так как в конце образуется упорядоченный бислой.
Информация о системе:
- Силовое поле используемое при построении топологии: fgmx
- Заряд системы: 0. Плюсы на холинах компенсируют свободные минусы фосфатов.
- Размер и форма ячейки: 6.2600 нм x 4.4430 нм x 5.7780 нм, прямоугольный параллелепипед.
- Минимизация энергии:
- Алгоритм минимизации энергии: l-bfgs
- Алгоритм расчёта электростатики и Ван-дер-Ваальсовых взаимодействий: Cut-off
- Модель, которой описывался растворитель: flexspc
- Утряска растворителя:
- Число шагов: 1000
- Длина шага: 0.0002
- Алгоритм расчёта электростатики (PME) и Ван-дер-Ваальсовых взаимодействий (Cut-off)
- Алгоритмы термостата (Berendsen) и баростата (no)
- Основной расчёт МД:
- Время моделирования: 50000 пс
- Число шагов: 10000000
- Длина шага: 0,005 пс
- Алгоритм интегратора: md
- Алгоритм расчёта электростатики (PME) и Ван-дер-Ваальсовых взаимодействий (Cut-off)
- Алгоритмы термостата (v-rescale) и баростата (Berendsen)