Разложение функции в ряд Фурье

Задание 1. Создание функции электронной плотности


На отрезке от 0 до 30 Å была смоделирована функция, состоящая из шести гауссовых кривых, соответствующих электронным плотностям атомов. Максимум плотности примерно пропорционален числу электронов в атоме. Атомы в молекулах ковалентно связаны и находятся на расстоянии ~1 Å друг от друга, молекулы удалены друг от друга на расстояние 3.9 Å. Функция получена при помощи скрипта compile-func.py следующей командой: 
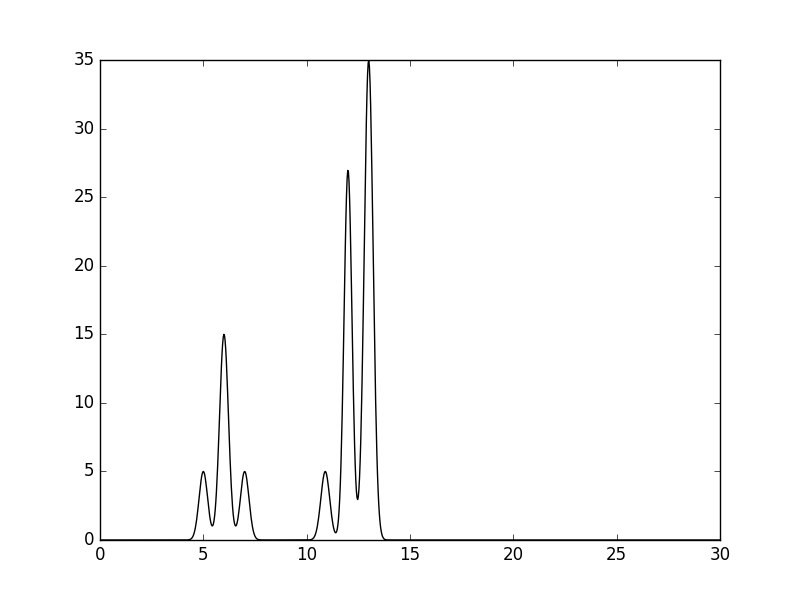
python compile-func.py -g 5,3.4,5+15,3.3,6+5,3.4,7+5,3.3,10.9+27,3.7,12+35,3.3,13
(генерация шести гауссовых функций с максимумами в точках 5, 6, 7, 10.9, 12, 13 и величинами пиков 5, 15, 5, 7, 27, 35). Результат работы скрипта - файл. График функции представлен на рис.1:

Рис.1. Функция электронной плотности для одномерного случая, смоделированная для двух молекул из трех атомов.


Задание 2. Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные.


Функция была разложена в ряд Фурье с помощью скрипта func2fourier.py. Команда 
python func2fourier.py -i func.txt -o series.txt
позволила получить файл с 499 гармониками в формате {[номер гармоники] [амплитуда] [фаза]}, которые в сумме дают исходную функцию.

Задание 3. Восстановление функции электронной плотности с удалением гармоник и добавлением шума.


Введем следующие критерии качества восстановленной функции:
  • Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов");
  • Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума;
  • Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно;
  • Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы";
Будем восстанавливать функцию электронной плотности при помощи скрипта fourier2func.py, и отбирать гармоники из полного набора с помощью fourier-filter.py. Для начала попробуем восстановить электронную плотность по всем имеющимся гармоникам:

python fourier2func.py -f func.txt -i series.txt
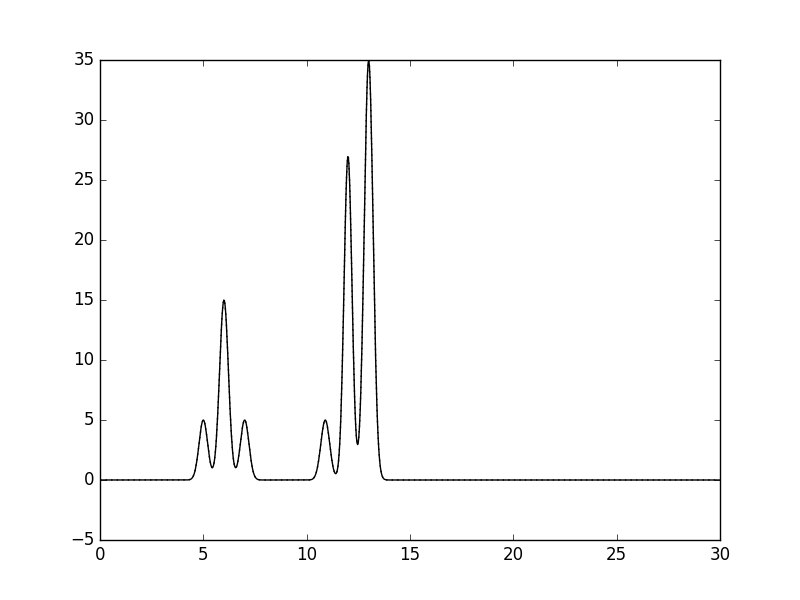
Рис.2. Исходная функция электронной плотности и восстановленная по полному набору гармоник.


Исходная и восстановленная функции полность совпадают. Теперь попробуем восстновить функцию по первым 1, 10, 15, 20, 25, 30, 40, 50, 60 и 65 гармоникам: 
python fourier-filter.py -r 0 -i series.txt -o ser0.txt 
python fourier2func.py -f func.txt -i ser0.txt -o serf0.txt 

python fourier-filter.py -r 0-10 -i series.txt -o ser10.txt 
python fourier2func.py -f func.txt -i ser10.txt -o serf10.txt 

python fourier-filter.py -r 0-15 -i series.txt -o ser15.txt 
python fourier2func.py -f func.txt -i ser15.txt -o serf15.txt 

python fourier-filter.py -r 0-20 -i series.txt -o ser20.txt 
python fourier2func.py -f func.txt -i ser20.txt -o serf20.txt 

python fourier-filter.py -r 0-30 -i series.txt -o ser30.txt 
python fourier2func.py -f func.txt -i ser30.txt -o serf30.txt 

python fourier-filter.py -r 0-40 -i series.txt -o ser40.txt 
python fourier2func.py -f func.txt -i ser40.txt -o serf40.txt 

python fourier-filter.py -r 0-50 -i series.txt -o ser50.txt 
python fourier2func.py -f func.txt -i ser50.txt -o serf50.txt 

python fourier-filter.py -r 0-60 -i series.txt -o ser60.txt 
python fourier2func.py -f func.txt -i ser60.txt -o serf60.txt 

python fourier-filter.py -r 0-65 -i series.txt -o ser65.txt 
python fourier2func.py -f func.txt -i ser65.txt -o serf65.txt

n_0: 0
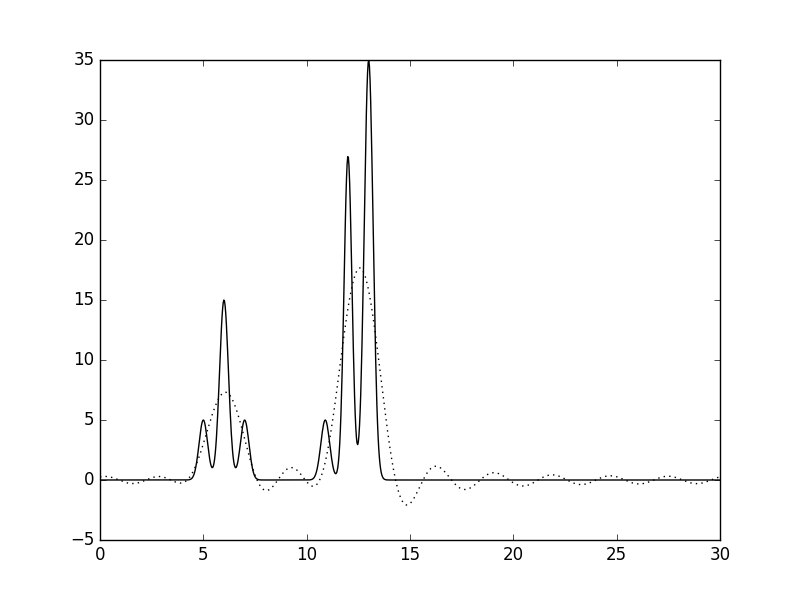n_0: 10
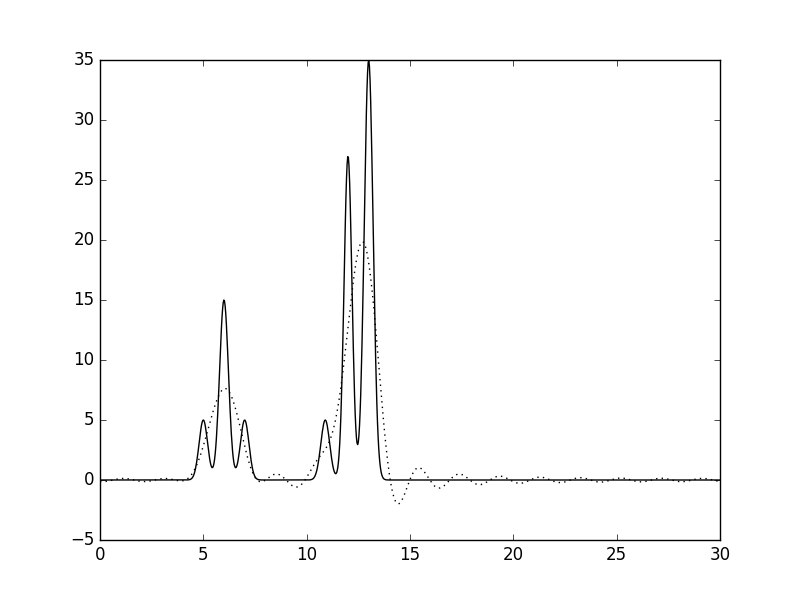n_0: 15

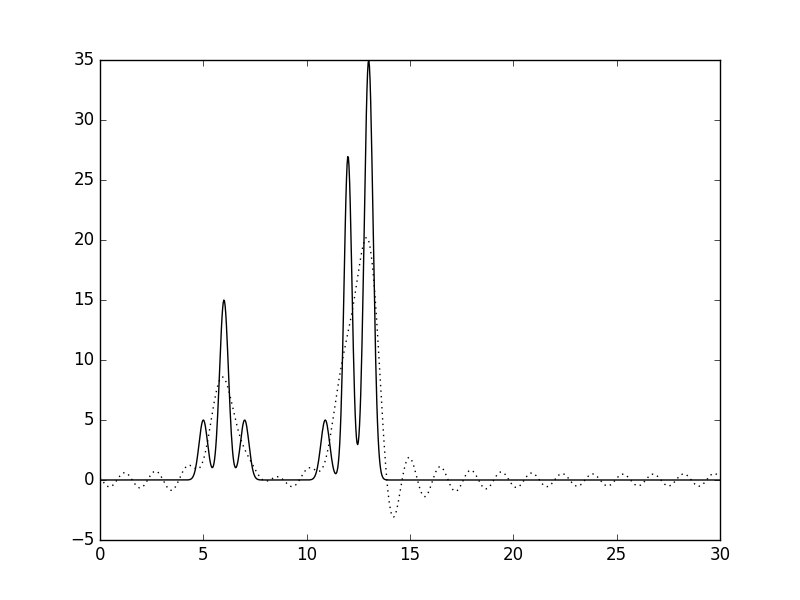n_0: 20
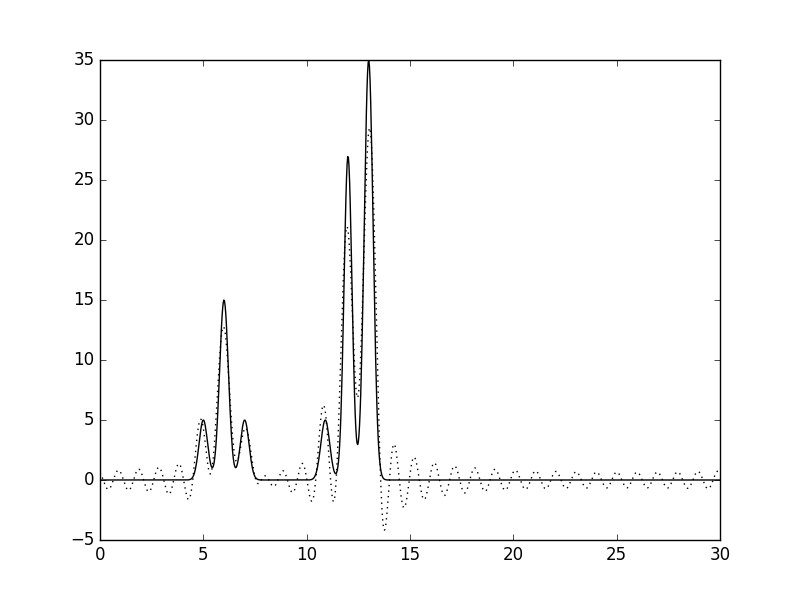n_0: 30
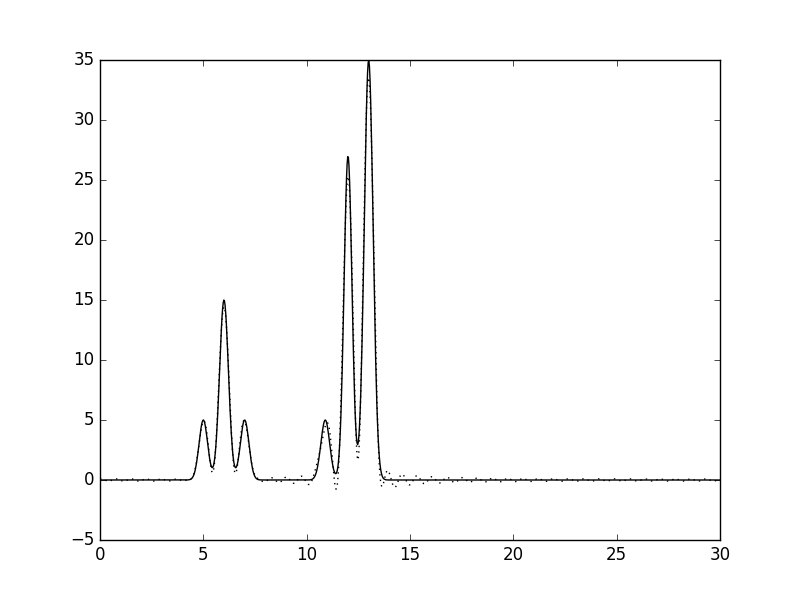n_0: 40

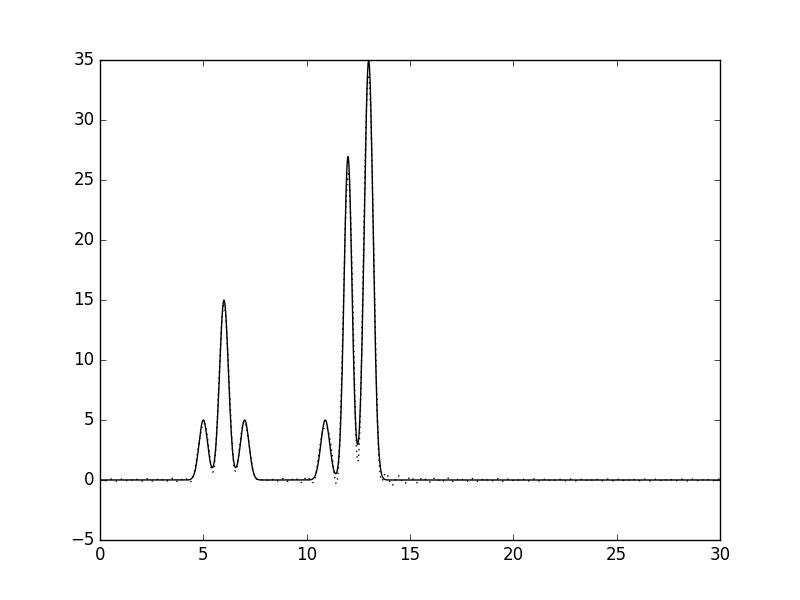n_0: 50
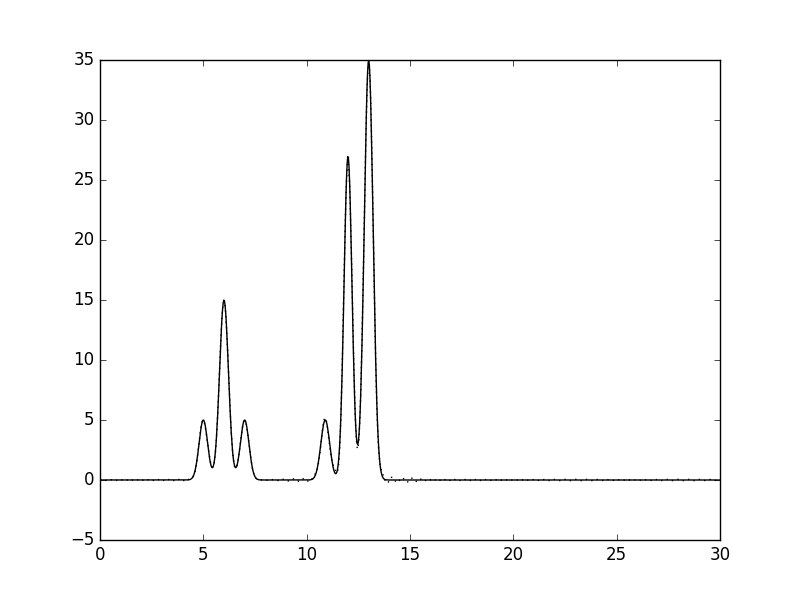n_0: 60
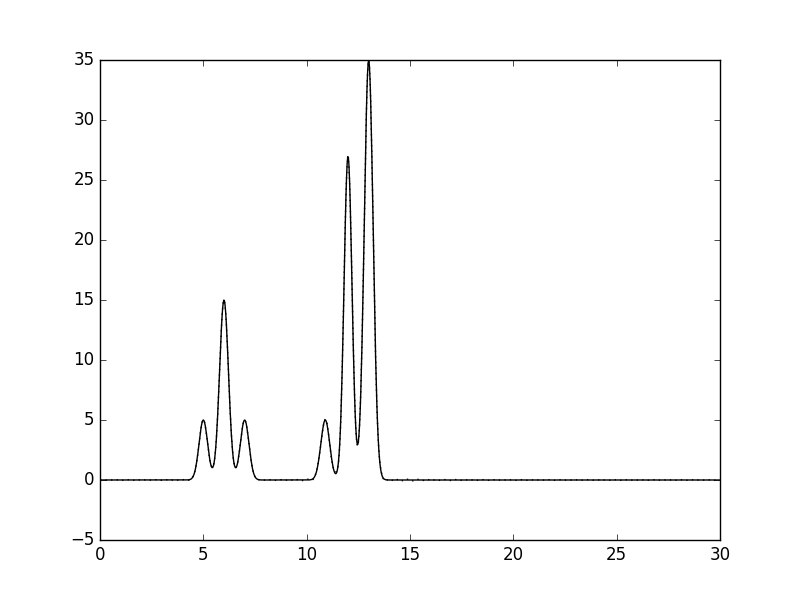n_0: 65
Таблица 1. Восстановленная функция электронной плотности (пунктир) при различном числе гармоник (n_0). Исходная функция - сплошная линия.

Согласно Таблице 1, по десяти гармоникам можно восстановить примерное положение центров молекул; по 30 гармоникам можно неточно определить положения атомов, а минимальный набор гармоник, необходимый для "отличного" восстановления функции - 41 Далее вся работа проводилась с этим набором.
Далее оценим влияние шума на восстановление функции: добавим 10% шума к
  • амплитуде:
 
python func2fourier.py -F 10 -i func.txt -o ser_noise_f.txt 
python fourier-filter.py -r 0-40 -i ser_noise_f.txt -o ser_noise_f_40.txt 
python fourier2func.py -f func.txt -i ser_noise_f_40.txt -o f40.txt


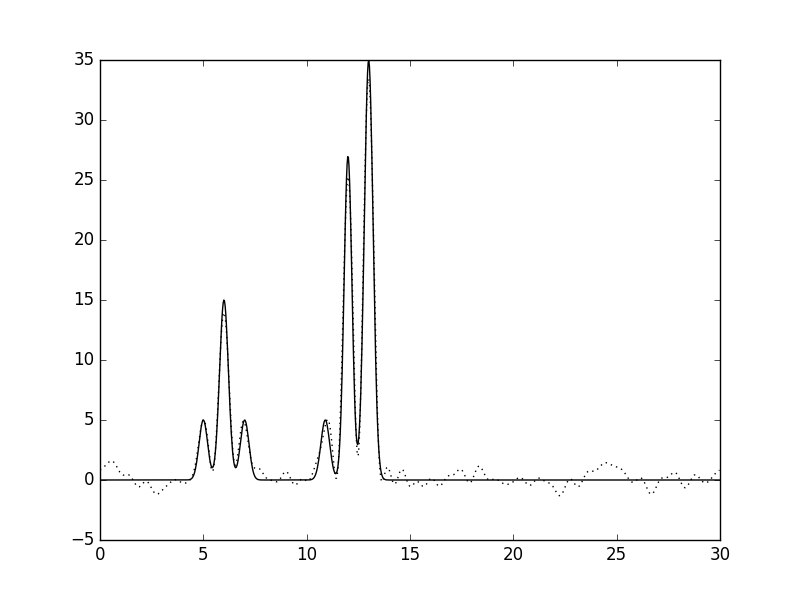
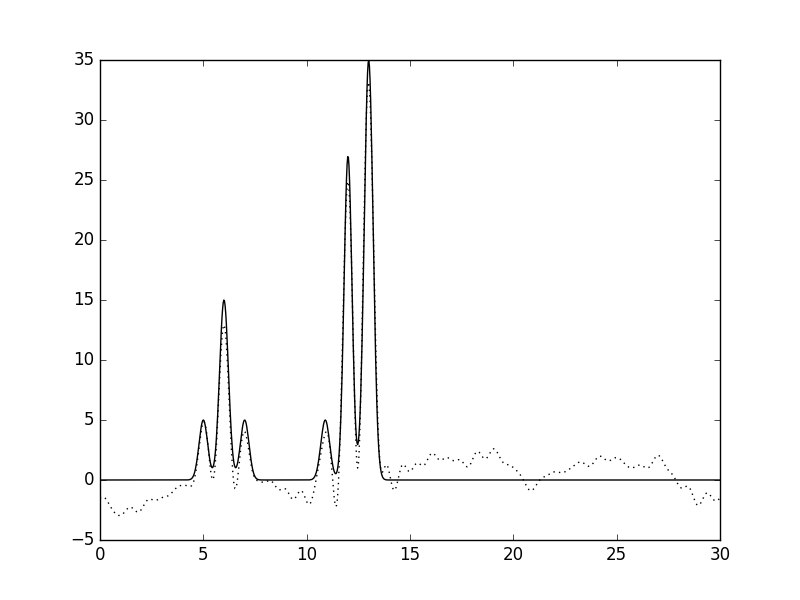
Рис.3. Гармоники 0-40, шум добавлен к амплитуде.

  • фазе:


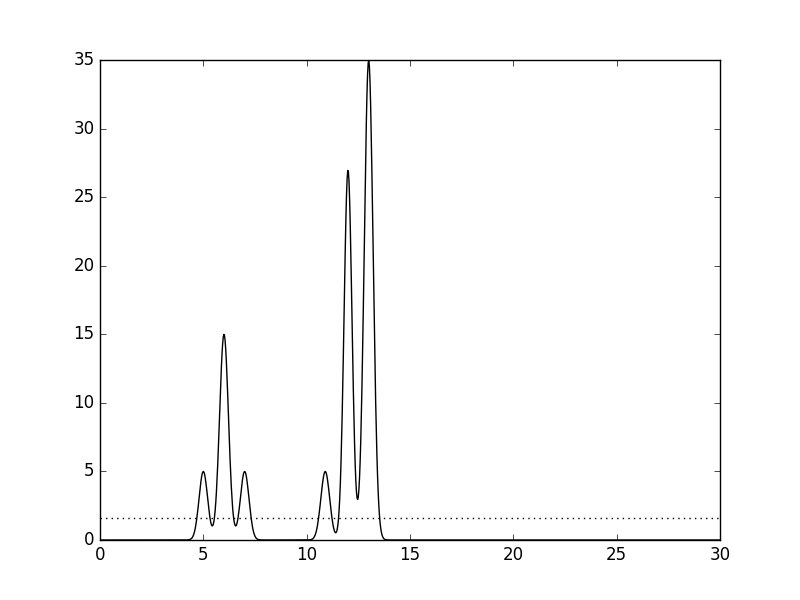
Рис.3. Гармоники 0-40, шум добавлен к фазе.


python func2fourier.py -P 10 -i func.txt -o ser_noise_p.txt 
python fourier-filter.py -r 0-40 -i ser_noise_p.txt -o ser_noise_p_40.txt 
python fourier2func.py -f func.txt -i ser_noise_p_40.txt -o p40.txt
  • и к фазе и амплитуде одновременно:
python func2fourier.py -F 10 -P 10 -i func.txt -o ser_noise_fp.txt 
python fourier-filter.py -r 0-40 -i ser_noise_fp.txt -o ser_noise_fp_40.txt 
python fourier2func.py -f func.txt -i ser_noise_fp_40.txt -o fp40.txt


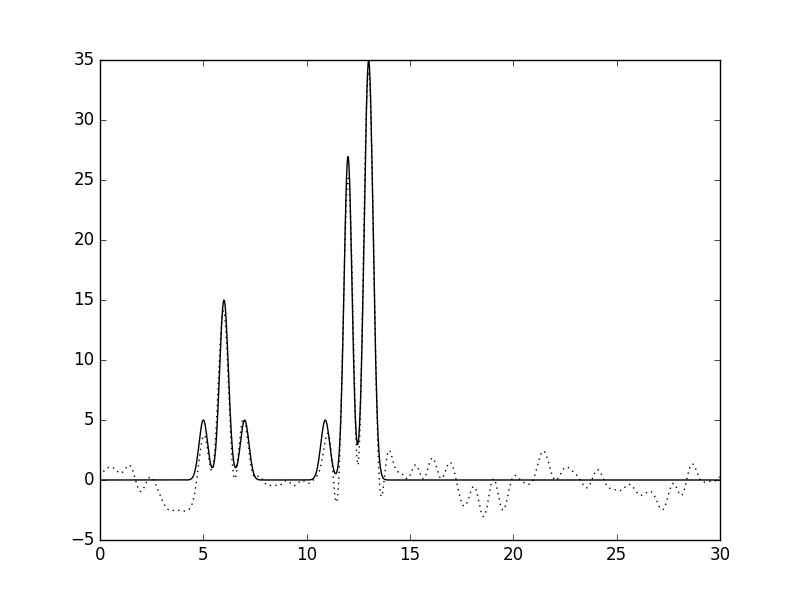
Рис.3. Гармоники 0-40, шум добавлен к амплитуде и фазе.

Можно заметить, что добавление шума к амплитуде почти не влияет на восстановление функции, в отличии от зашумления фазы.

Наконец, проанализируем, как функция восстанавливается по неполному набору гармоник (как это и происходит в условиях реального эксперимента).


Сначала удалим первую, первые две и первые три гармоники: 
python fourier-filter.py -r 1-40 -i series.txt -o ser1_40.txt 
python fourier2func.py -f func.txt -i ser1_40.txt -o 1_40.txt

python fourier-filter.py -r 2-40 -i series.txt -o ser2_40.txt 
python fourier2func.py -f func.txt -i ser2_40.txt -o 2_40.txt

python fourier-filter.py -r 3-40 -i series.txt -o ser3_40.txt 
python fourier2func.py -f func.txt -i ser3_40.txt -o 3_40.txt


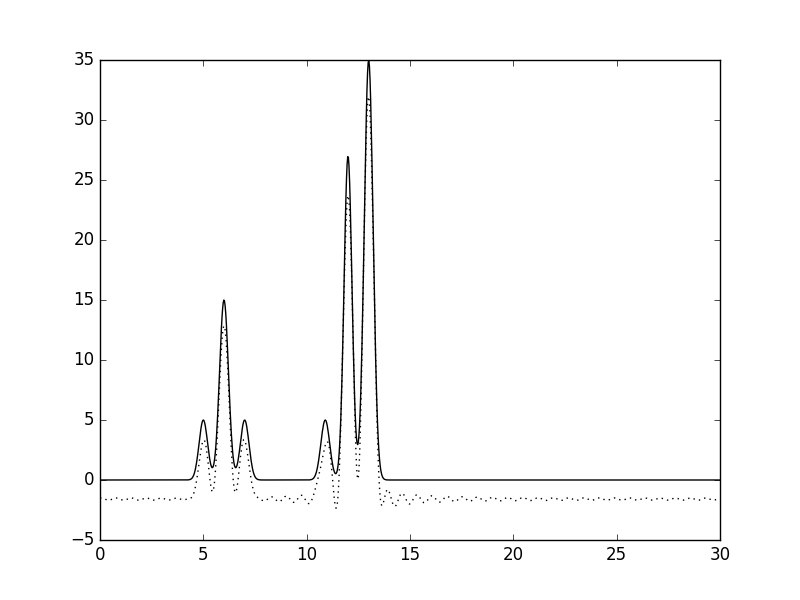
Рис.4. Гармоники 1-40.


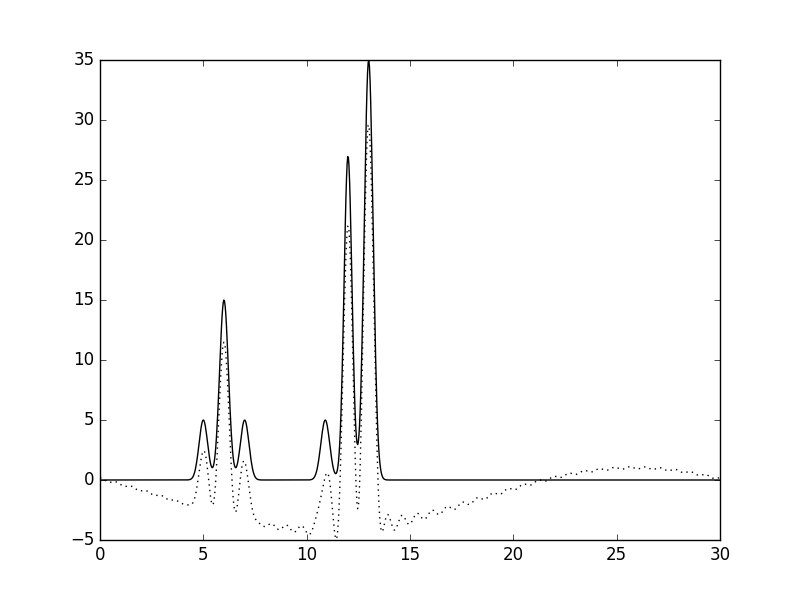
Рис.5. Гармоники 2-40.


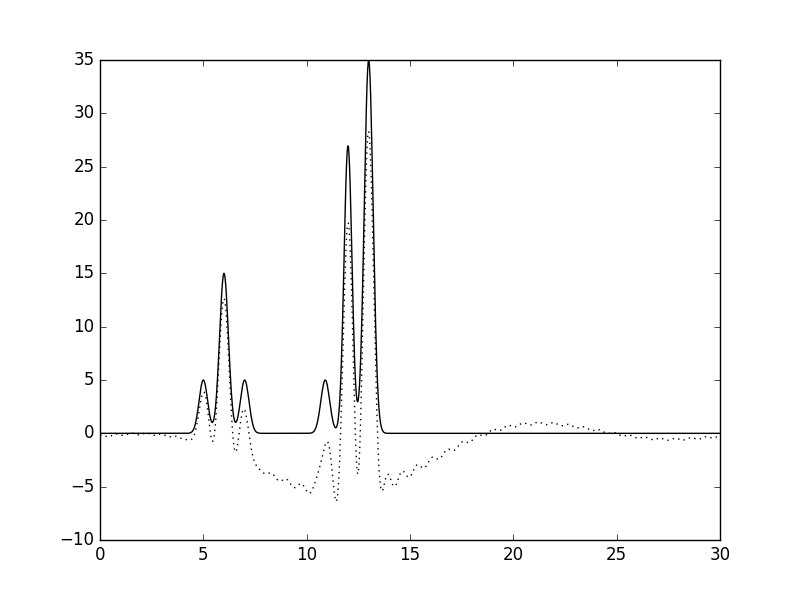
Рис.6. Гармоники 3-40.

При удалении первой гармоники функция заметно смещается вниз по оси ординат, что можно объяснить тем, что значение первой (нулевой) гармоники равняется первому коэффициенту ряда Фурье. Если удалить первые две или три гармоники, то от функции вычитается синусоида с возрастающим периодом.
Теперь удалим 4 и 8 гармоник из середины набора: 
python fourier-filter.py -r 0-17,23-40 -i series.txt -o sermid1.txt 
python fourier2func.py -f func.txt -i sermid1.txt -o mid1.txt

python fourier-filter.py -r 0-15,25-40 -i series.txt -o sermid2.txt 
python fourier2func.py -f func.txt -i sermid2.txt -o mid2.txt


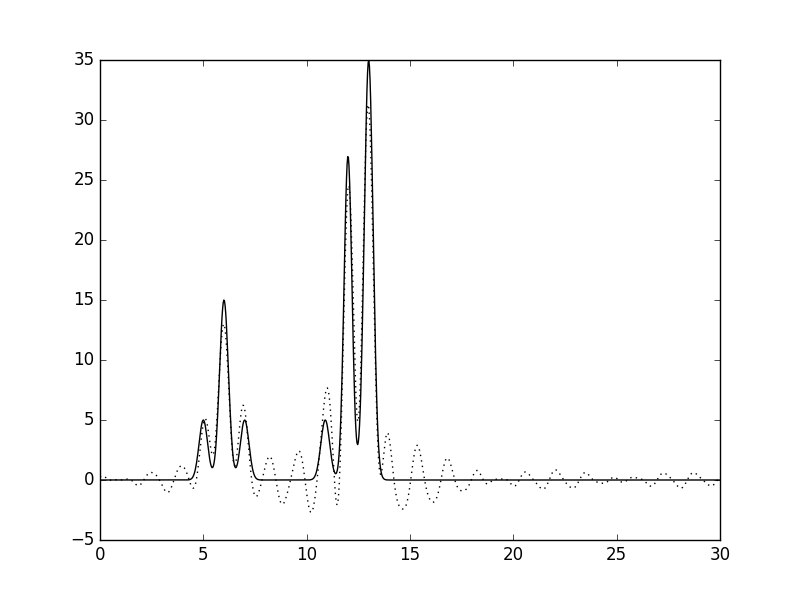
Рис.7. Гармоники 0-17,23-40.


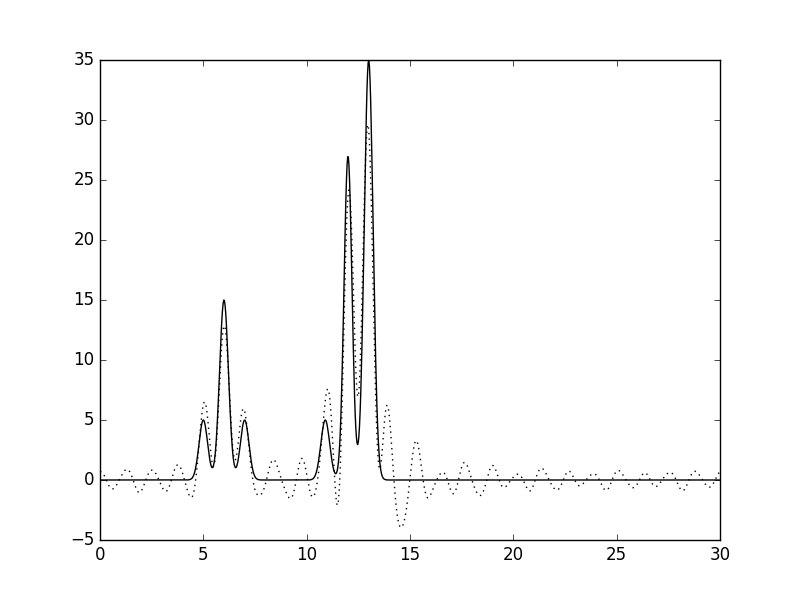
Рис.8. Гармоники 0-15,25-40.

Качество восстановления заметно ухудшилось.
Теперь добавим гармонику с номером n_0+10: 
python fourier-filter.py -r 0-40,50 -i series.txt -o serend.txt 
python fourier2func.py -f func.txt -i serend.txt -o end.txt


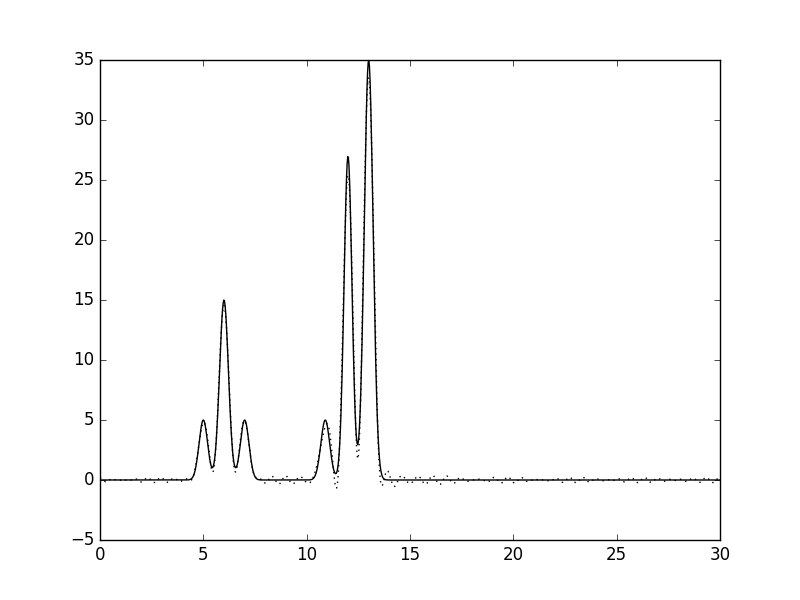
Рис.9. Гармоники 0-40,50.

Добавление 50-й нармоники почти не повлияло на качество восстановления. Исходя из вышерассмотренного, можно сдлеать вывод, что при восстановлении функции наиболее значимый вклад восят гармоники, находящиеся в середине набора 0-n_0.

Задание 3. Результаты



Таблица 1. Восстановление функции электронной плотности по разложению в ряд Фурье
Набор гармоник Разрешение, Å Полнота данных (%) Шум амплитуды (% от F) Шум фазы (% от φ) Качество восстановления
Полный набор гармоник без шумов
0-498 0.06 100 0 0 отличное
0 - 100 0 0 плохое
0-10 2.7 100 0 0 плохое
0-15 1.875 100 0 0 плохое
0-20 1.4 100 0 0 среднее
0-30 0.96 100 0 0 хорошее
0-40 0.73 100 0 0 отличное
0-50 0.58 100 0 0 отличное
0-60 0.49 100 0 0 отличное
0-65 0.45 100 0 0 отличное
Полный набор гармоник с шумами
0-40 0.73 100 10 0 хорошее
0-40 0.73 100 0 10 среднее
0-40 0.73 100 10 10 среднее
Неполный набор гармоник
1-40 0.73 97.5 0 0 отличное
2-40 0.73 92.8 0 0 отличное
3-40 0.73 92.6 0 0 отличное
0-17, 23-40 0.73 90.2 0 0 плохое
0-15, 25-40 0.73 80.4 0 0 плохое
0-40, 50 0.58 82.3 0 0 отличное


Назад к странице семестров

© Andrew Sigorskih,2017.