Молекулярная динамика биологических молекул в GROMACS:
Моделирование самосборки липидного бислоя и анализ результатов

Для получения исходной структуры набора липидов на kodomo были выполнены следующие команды:

In [ ]:
# получим файлы
wget http://kodomo.cmm.msu.ru/~golovin/bilayer/dppc.itp
wget http://kodomo.cmm.msu.ru/~golovin/bilayer/lipid.itp
wget http://kodomo.cmm.msu.ru/~golovin/bilayer/dppc.gro
wget http://kodomo.cmm.msu.ru/~golovin/bilayer/b.top
wget http://kodomo.cmm.msu.ru/~golovin/bilayer/em.mdp
wget http://kodomo.cmm.msu.ru/~golovin/bilayer/pr.mdp
wget http://kodomo.cmm.msu.ru/~golovin/bilayer/md.mdp
    
# создадим ячейку
genconf -f dppc.gro -o b_64.gro -nbox 4 4 4

# c помощью editconf преобразуем dppc.gro и b_64.gro в pdb файлы
editconf -f b_64.gro -o b_64.pdb
editconf -f dppc.gro -o dppc.pdb

# В текстовом редакторе в файле b.top установили правильное количество липидов в системе
mcedit b.top

# Сделаем небольшой отступ в ячейке от липидов, что бы добавить примерно 2500 молекул воды
editconf -f b_64.gro -o b_ec -d 0.5

# Проведём оптимизацию геометрии системы, что бы удалить "плохие" контакты молекул
grompp -f em -c b_ec -p b -o b_em -maxwarn 2
mdrun -deffnm b_em -v

# Cтоит отметить изменение максимальной силы в ходе оптимизации геометрии:
# от 4.37970е+05 на шаге 0 до 6.16887е+02 на шаге 51

# Добавим в ячейку молекулы воды типа spc
genbox -cp b_em -p b -cs spc216 -o b_s

# Проведём "утряску" воды:
grompp -f pr -c b_s -p b -o b_pr -maxwarn 1
mdrun -deffnm b_pr -v

# Переформатируем b_pr.gro и b_s.gro в pdb формат
editconf -f b_pr.gro -o b_pr.pdb
editconf -f b_s.gro -o b_s.pdb
рис.1. Молекула дипальмитоилфосфатидилхолина из файла dppc.gro
рис.2. Ячейка из 64 липидов, файл b_64.gro
рис.3. Система до утряски воды, файл b_s.gro
рис.4. Система после утряски воды, файл b_pr.gro

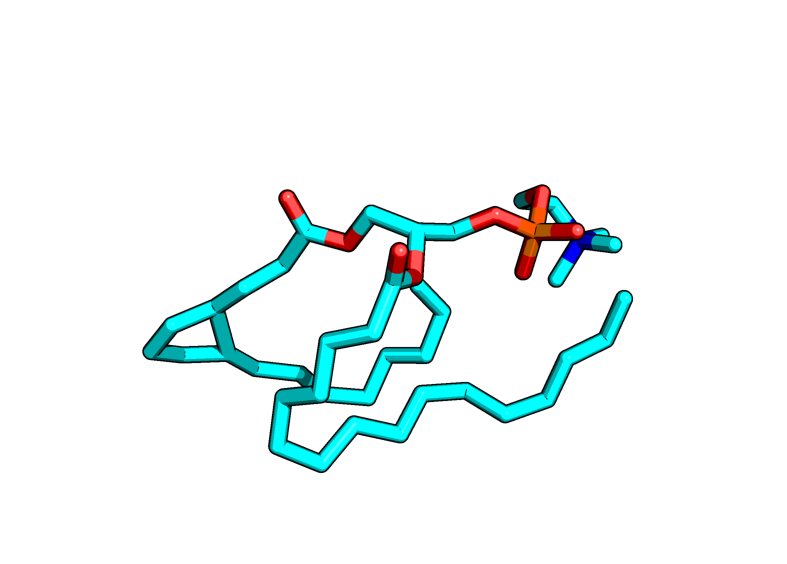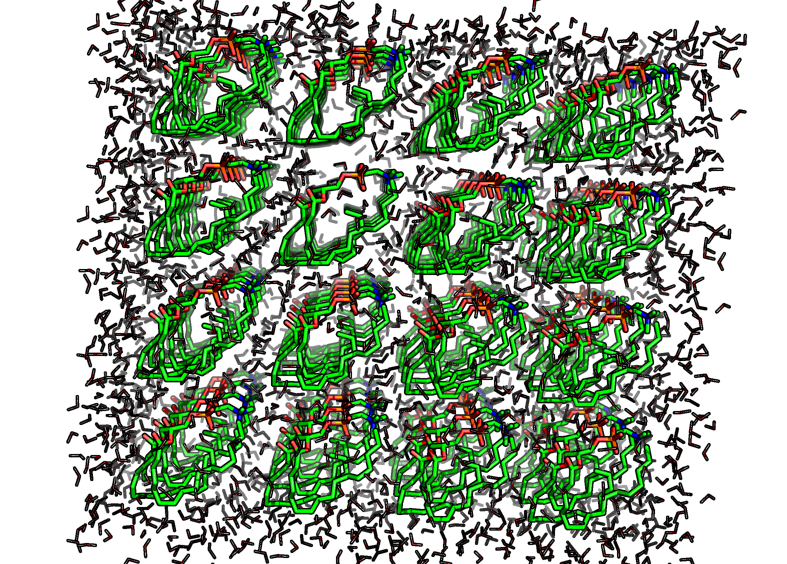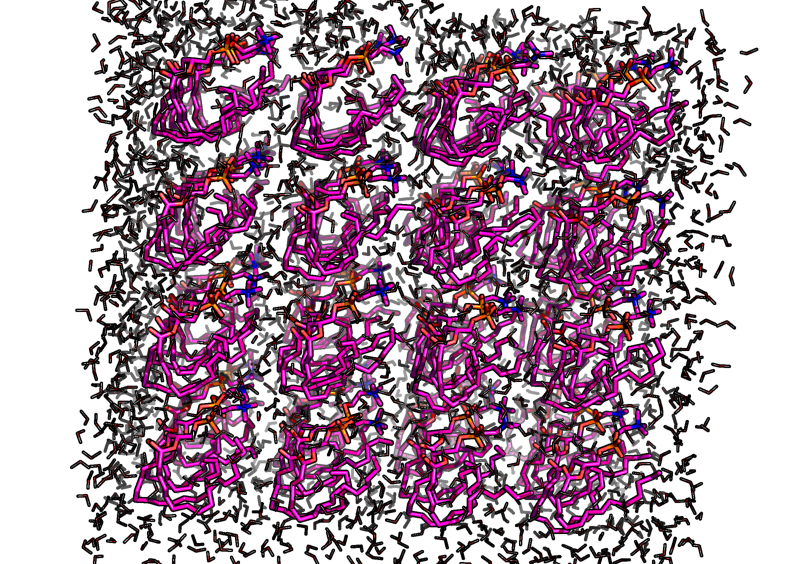Видим, что после утряски липидный параллелипипед стал более расхлябанным, гидрофобные хвосты теперь висят как попало.


На суперкомпьютере "Ломоносов" было запущено моделирование системы:

sbatch -N1 --ntasks-per-node=2 -e error-gpu.log -o output.log -t 350 -p gpu impi /opt/ccoe/gromacs-5.0.4/build/bin/gmx_mpi mdrun -testverlet -deffnm b_md -v

Анализ результатов моделирование самосборки липидного бислоя

In [3]:
# Любой анализ начинают с визуального анализа движений молекул. При вопросе о выводк групп выберите DPPC
trjconv -f b_md.xtc -s b_md.tpr -o b_pbc_1.pdb -skip 20
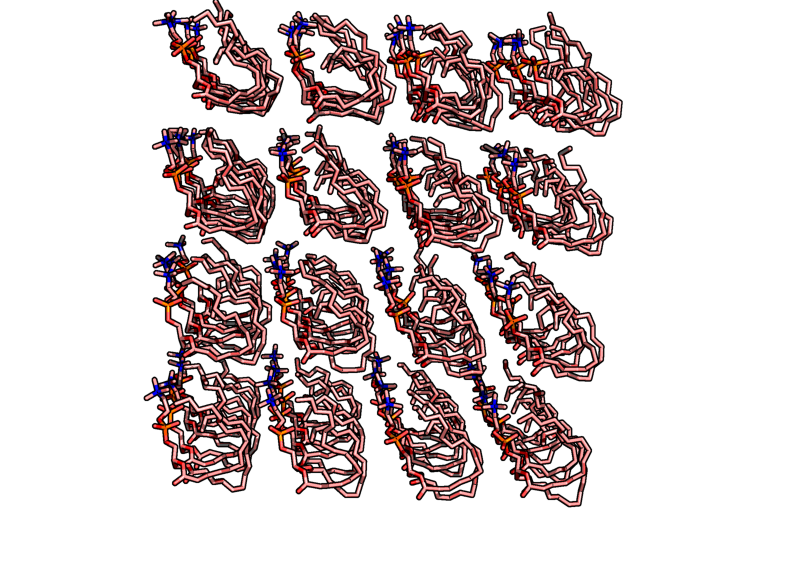рис.5. С виду вполне красивая система превращается...
рис.6. в непонятное месиво(

Попробуем выставить Periodic Boundary Conditions при помощи опции -pbc mol:

In [ ]:
trjconv -f b_md.xtc -s b_md.tpr -o b_pbc_2.pdb -skip 20 -pbc mol

рис.7. Успех! Даже получили что-то, частично похожее на бислой - только одному кусочку не повезло и его выкинуло наверх

Система организуется в мицеллоподобную структуру с самого начала моделирования, однако нечно похожее на бислой наблюдается на начиная с фрейма 35. Из pdb файла найдем время образования этой модели: 17000.00

рис.8. Фрейм 35. Видим начало формирования бислоя из мицеллы.

Определим площадь занимаемую одним липидом.

In [ ]:
import pandas as pd
In [ ]:
# размеры ячейки из траектории
g_traj -f b_md.xtc -s b_md.tpr -ob box_1.xvg
In [35]:
with open('box_1.xvg', 'r') as f:
    lines = [item.strip('\n') for item in f.readlines() 
             if (not item.startswith("@")) and (not item.startswith("#"))]
times = [item.split('\t')[1] for item in lines]
sq = [float(item.split('\t')[3]) * float(item.split('\t')[4]) / 32 for item in lines]
In [37]:
data = pd.DataFrame({'times':times, 'Squares':sq})
data.head()
Out[37]:
Squares times
0 0.802239 0
1 0.805102 25
2 0.806373 50
3 0.810335 75
4 0.815054 100
In [38]:
data.plot(x="times", y = "Squares")
plt.show()

Видим, что площадь, занимаемая средним липидом, с течением времени уменьшается за счет того, что липиды компактизуются в пространстве и укладываются в бислой. Даже испортивший нам всю картину кусок тоже относительно хорошо собран для одного слоя.


Теперь пределим изменение гидрофобной и гидрофильной поверхности в ходе самосборки:

In [ ]:
g_sas -f b_md.xtc -s b_md.tpr -o sas_b.xvg

Нормаль к поверхность это ось Х

In [31]:
with open("sas_b.xvg", 'r') as f:
    lines = [item.strip('\n') for item in f.readlines() 
             if (not item.startswith("@")) and (not item.startswith("#"))]
times = [int(item.split()[0]) for item in lines]
hphob = [float(item.split()[1]) for item in lines]
hphil = [float(item.split()[2]) for item in lines]
In [32]:
data = pd.DataFrame({'times':times, 'Hydrophobic':hphob, 'Hydrophilic':hphil})
In [33]:
data.head()
Out[33]:
Hydrophilic Hydrophobic times
0 131.232 202.648 0
1 132.714 197.694 25
2 136.555 195.547 50
3 136.956 191.287 75
4 141.580 192.608 100
In [34]:
data.plot(x="times", y = ["Hydrophobic", "Hydrophilic"])
plt.show()

Вначале гидрофобная поверхность системы максимально: липиды лежат в ячейке отдельно, при этом стоит помнить и про возникшую при утряске системы с водой "расхлябанность". Однако это состояние крайне невыгодно, и система очень быстро (уже на втором фрейме) начинает скатываться в мицеллоподобную структуру, а затем утрясывается до бислоя, при этом гидрофобная поверхнсть продолжает уменьшаться (однако выитый наружу кусок немного ее увеличивает к концу). Гидрофильная повперхность всё это время выше, но она тоже несколько снижается из-за компактизации липидов в бислое.


Теперь оценим меру порядка в начале и в конце траектории:

In [ ]:
wget http://kodomo.cmm.msu.ru/~golovin/bilayer/sn1.ndx
# начало
g_order -s b_md -f b_md.xtc -o ord_start.xvg -n sn1.ndx -e 5000 -d X

# конец 
g_order -s b_md -f b_md.xtc -o ord_end.xvg -n sn1.ndx -b 45000 -d X
In [40]:
with open("ord_start.xvg", 'r') as f:
    lines = [item.strip('\n') for item in f.readlines() 
             if (not item.startswith("@")) and (not item.startswith("#"))]
xax = [int(item.split()[0]) for item in lines]
start = [float(item.split()[2]) for item in lines]

with open("ord_end.xvg", 'r') as f:
    lines = [item.strip('\n') for item in f.readlines() 
             if (not item.startswith("@")) and (not item.startswith("#"))]
end = [float(item.split()[2]) for item in lines]
In [41]:
data = data = pd.DataFrame({'xax':xax, 'Start_order':start, 'End_order':end})
data.head()
Out[41]:
End_order Start_order xax
0 -0.051353 -0.007330 1
1 -0.073848 -0.004933 2
2 -0.088481 -0.007688 3
3 -0.090587 -0.006301 4
4 -0.094305 -0.001805 5
In [42]:
data.plot(x="xax", y = ["Start_order", "End_order"])
plt.show()

В начале траектории значения меры порядка сильно колебаются, что можно объяснить с хаотичностью движений молекул липидов. В конце траектории видно, что сначала липиды довольно сильно теряют подвижность в силу организации их в бислой, однако потом выбивается тот самый кусок, испортившй нам картину, и подвижность тут же резко возрастает.

Основные сведения о системе

  • Силовое поле используемое при построении топологии топологии - ffgmx
  • Заряд системы - 0.000 (всё протонировано?)
  • Размер и формa ячейки - прямоугольный параллелепипед со сторонами 6.2600, 4.4430 и 5.7780 нм.
  • Минимизация энергии:
      • Алгоритм минимизации энергии - l-bfgs
      Алгоритм расчёта электростатики и Ван-дер-Ваальсовых взаимодействий - Cut-off
  • Модель, которой описывался растворитель - flexspc
  • Утряска растворителя:
      • Число шагов - 1000
      Длина шага - 0.0002
      Алгоритм расчёта электростатики и Ван-дер-Ваальсовых взаимодействий - pme, Cut-off
      Алгоритмы термостата и баростата - Berendsen, no
  • Основной расчёт МД:
      • Время моделирования - 50000.00
      Длина траектории - 50 ns
      Число шагов - 10000000
      Длина шага - 0,005 ps
      Алгоритм интегратора - md
      Алгоритмы расчёта электростатики и Ван-дер-Ваальсовых взаимодействий - pme, Cut-off
      Алгоритмы термостата и баростата - v-rescale, Berendsen

Назад к странице семестров