На страницу 3 семестра

Эволюционные расстояние между последовательностями

g0 g1 g2 g3 g4 a b c d e f
g0 0 70 50 65 60 100 100 90 90 100 100
g1 — 0 120 135 130 30 30 160 160 170 170
g2 — — 0 15 10 150 150 40 40 50 50
g3 — — — 0 25 165 165 25 25 65 65
g4 — — — — 0 160 160 50 50 40 40
a — — — — — 0 60 190 190 200 200
b — — — — — — 0 190 190 200 200
c — — — — — — — 0 50 90 90
d — — — — — — — — 0 90 90
e — — — — — — — — — 0 80
g — — — — — — — — — — 0
Слева представлена треугольная матрица расстояний между нуклеотидными последовательностями, полученными ранее (см. Эволюционную модель).

Матрица попарного различия: среднее число несовпадающих нуклеотидов на 100 позиций

g0 g1 g2 g3 g4 a b c d e f
g0 0.00 34.54 30.93 37.97 35.22 45.02 46.91 46.91 46.22 47.08 48.45
g1 — 0.00 49.48 54.30 52.41 20.10 19.93 59.11 59.62 60.65 61.17
g2 — — 0.00 11.86 7.56 54.64 57.39 27.66 26.12 28.18 30.58
g3 — — — 0.00 19.07 58.25 60.82 17.35 16.49 34.88 39.18
g4 — — — — 0.00 56.01 59.97 33.16 32.13 24.23 24.91
a — — — — — 0.00 35.57 61.34 63.40 61.51 64.09
b — — — — — — 0.00 63.06 63.92 66.15 65.46
c — — — — — — — 0.00 29.04 45.19 47.08
d — — — — — — — — 0.00 45.36 48.80
e — — — — — — — — — 0.00 40.03
g — — — — — — — — — — 0.00
    Матрица, представленная слева, получена при помощи программы distmat пакета EMBOSS. При этом выравнивания были сделаны без вставок и делеций (т.к. их не предусматривает наша модель эволюции): последовательности были просто написаны друг под другом. Программа distmat использовалась без коррекции расстояний (с параметром uncorrected distances).

Матрица попарных эволюционных расстояний, вычисленных по методу Джукса - Кантора

g0 g1 g2 g3 g4 a b c d e f
g0 0.00 46.28 39.87 52.94 47.57 68.76 73.65 73.65 71.84 74.11 77.89
g1 — 0.00 80.871 96.541 89.981 23.403 23.173 116.37 118.84 124.05 126.79
g2 — — 0.00 12.90 7.97 97.79 108.67 34.52 32.10 35.34 39.29
g3 — — — 0.00 22.01 112.42 124.95 19.74 18.63 46.92 55.41
g4 — — — — 0.00 103.03 120.54 43.78 41.95 29.26 30.28
a — — — — — 0.00 48.22 127.73 140.00 128.68 144.58
b — — — — — — 0.00 137.81 143.41 160.29 154.68
c — — — — — — — 0.00 36.73 69.20 74.11
d — — — — — — — — 0.00 69.63 78.87
e — — — — — — — — — 0.00 57.23
g — — — — — — — — — — 0.00
    Эта матрица была получена на основе того же множественного выравнивания, что и предыдущая, при помощи той же программы distmat. Но была применена формула Джукса – Кантора (JC).

Сравнение 2 методов определения эволюционных расстояний





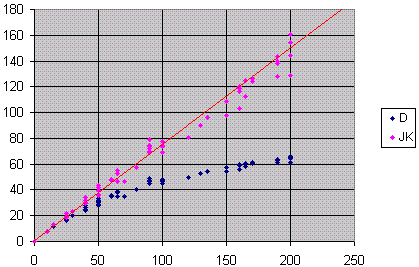
  • По оси x отложено количество мутаций, сделанных программой msbar (что в 4/3 раза более истиного расстояния, т.к. замену нуклеотида сам на себя программа считает мутацией)
  • По оси y отложены:
    1. Синим цветом — расстояния между последовательностями согласно методу неоткорректированных расстояний (D)
    2. Розовым — расстояния между ними же согласно формуле Джукса – Кантора (JC).
    3. Красным цветом — линия y = 0.75x (истинные расстояния)
Расстояния указаны в количестве мутаций на 100 п.н.
Работа проводилась в Microsoft Excel.

    Итак, мы видим, что формула Джукса – Кантора даёт почти идеально верные результаты при малых расстояниях между последовательностями, а при больших (до 200 мутаций) – небольшие отклонения. Метод неоткорректированных расстояний даёт хорошие результаты на расстояниях до 40 нуклеотидов, а при больших расстояниях сильно занижает результат, асциллируя при стремлении расстояния к бесконечности у прямой y = 0.75.

© Лев Шагам,2005