Айдарханов Руслан ФББ - Abinitio вычисления для нафталина и азулена

Была предоставлена оптимизированная структура этана в виде z-matrix:
```
 $DATA
eth
C1
 C   
 C      1   cc 
 H      2   ch   1   cchv 
 H      2   ch   1   cch   3   d1 0
 H      2   ch   1   cch   3   d2 0
 H      1   ch   2   cch   3   d3 0
 H      1   ch   2   cch   5   d3 0
 H      1   chv  2   cch   4   d3 0

cc=1.52986
ch=1.08439
chv=1.08439
cch=111.200
cchv=111.200
d1=120
d2=-120
d3=180
 $END
```
Наша цель состоит в том, что бы создать порядка 20 разных файлов для расчёта энергии в Gamess с разными значениями по длине одной из связей. Автоматизируем процесс с помощью скрипта на bash.
Файл-заготовка для размножения: et.inp. Для этого к координатам добавляем шапку для dft из предыдущего практикума. Только надо изменить информацию о типе входных координат: замените COORD=CART на COORD=ZMT.
Создаём скрипт, который будет генерировать необходимые файлы, выполнять для них расчёт с помощью GAMESS и выводить значения энергии для каждого файла.
make_b.bash
Запускаем скрипт командой и сразу же перенаправляем выход в файл bond.txt:
```
bash ./make_b.bash > bond.txt
```
Запускаем Xming для Putty и присоединяемся к kodomo. Переходим в рабочую директорию и запустите Gnuplot:
```
gnuplot
```
Построим зависимость энергии от длины связи: plot "bond"
Появился график с точками похожими на параболу. Теперь нам надо найти коэффициенты в функции f(x)=a+k(x-b)^2 которые бы позволили наиболее близко описать наблюдаемую зависимость. Для этого воспользуемся возможностями Gnuplot. Сначала зададим функцию в развернутом виде, в строке gnuplot введём:
```
f(x)=a + k*x*x - 2*k*x*b + k*b*b 
```
И зададим стартовые значения коэффициентов:
```
a=-80
k=1
b=1.5
```
Проведём подгонку коэффициентов под имеющиеся точки в файле bond.txt:
```
fit f(x) "bond.txt" via a,k,b 
```
Значения коэффициентов: bond_param.txt. Построим графики функции и значений энергии из Gamess.
```
plot "bond.txt", f(x)
```
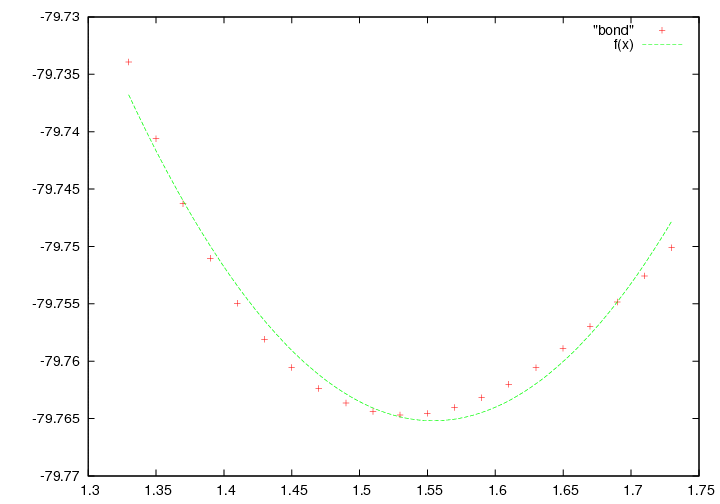
Функция неточно совпадает с точками, так как в данном случае мы наблюдаем участок потенциала Мориса, имеющий более сложную зависимость.
Проделаем аналогичные операции для валентного угла HCC, его значения должны изменяться от 109.2 до 113.2. Апроксимируем зависимость так же параболой:
```
f(x)=a + k*x*x - 2*k*x*b + k*b*b
```
Скрипт: make_v.bash
Энергии: valent.txt
Значения коэффициентов: valent_param.txt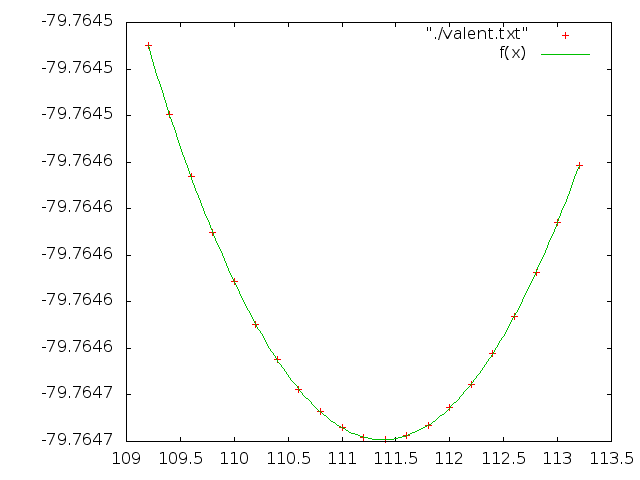

Очень хорошая апроксимация, все точки на параболе.
Проделаем аналогичные операции для торсионного угла d3, его значения должны изменяться от -180 до 180 c шагом 12. Зависимость в данном случае неплохо апроксимируется косинусом:
```
f(x)=a*cos(k*x/180*pi) + b
```
Скрипт: make_t.bash
Энергии: tors.txt
Значения коэффициентов: tors_param.txt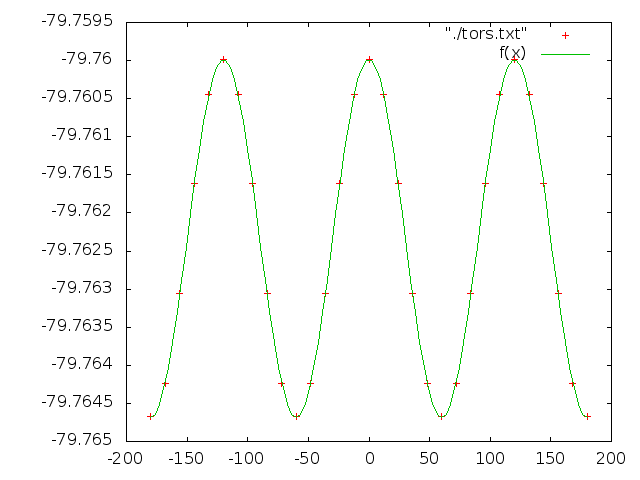

Мы имеем 3 минимума, а не 4, так как крайние точки совпадают (углы -180 и 180).
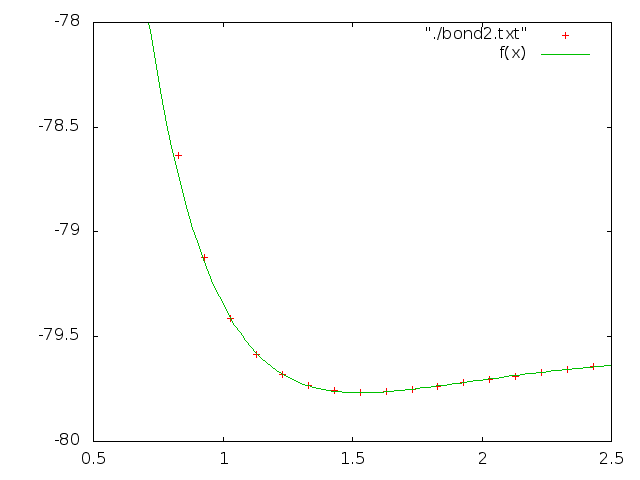
* Увеличим шаг до 0.1 ангстрема при расчёте связи. Данная зависимость описывается потенциалом Мориса:
```
f(x)=d*(1-exp(-a*(r-re)))*(1-exp(-a*(r-re))) + f
```
Значение для re возьмём оптимальное: re=1.52986.
Скрипт: make_b2.bash
Энергии: bond2.txt
Значения коэффициентов: bond2_param.txt

Abinitio вычисления для нафталина и азулена

© Айдарханов Руслан 2008