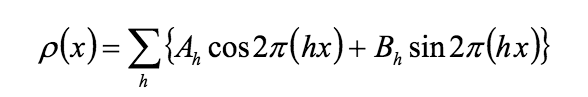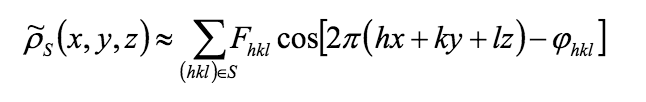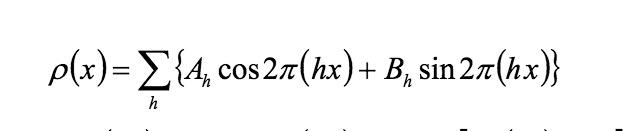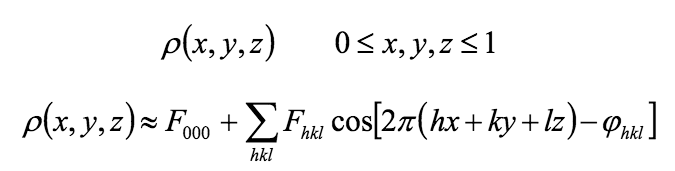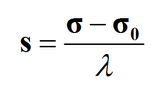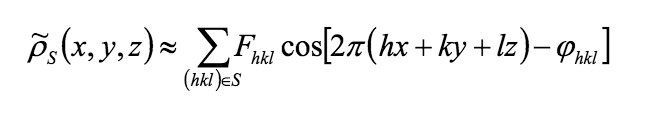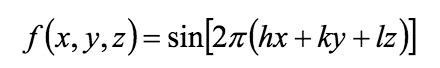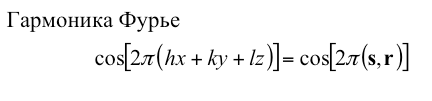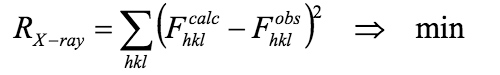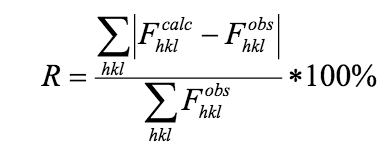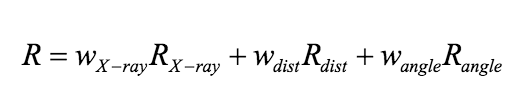Вопросы к коллоквиуму

Этапы расшифровки

1. Перечислите основные этапы определения структуры методом РСА.

   1. Выделение и очистка белка.
   2. Кристаллизация.
   3. Дифракционный эксперимент.
   4. Решение фазовой проблемы.
   5. Расчет и интерпретация синтеза Фурье, построение предварительной модели.
   6. Уточнение атомной модели.

   7. Проверка правильности модели.

Электронная плотность

1. Дайте определение функции электронной плотности (для объекта, состоящего из молекул и атомов).

   Функция электронной плотности – это функция на пространстве, значение которой равно среднему (по времени) заряду в элементарном объеме.
   
   Среднее по времени число электронов, обнаруживаемых в маленькой окрестности точки, деленное на объем окрестности. Точное определение: предел этой величины при стремлении объема окрестности к нулю. Электронная плотность в центре атома максимальна.

2. В каких физических единицах измеряется функция электронной плотности?
   
   Функция электронной плотности измеряется в числе электронов в единице объема.
   
3. Опишите характер графика зависимости электронной плотности для одного атома.
   
   Правая «половина» гауссового «колокола».
   
   

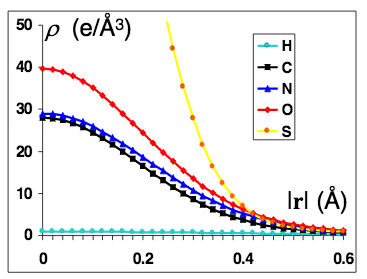
4. Как изображается функция электронной плотности в pymol? Какие условные единицы используются при изображении электронной плотности в компьютере?
   
   В виде изоповерхности для определенного уровня подрезки, который измеряется в терминах среднеквадратичных отклонений.

Кристалл

1. Что такое симметрия объекта, состоящего из молекул и атомов?
   
   Это преобразование, которое задается матрицей вращения и вектором трансляции. Их применение превращает объект в идентичный.
   
2. Что такое трансляционная симметрия? Как идеализируется физический объект, обладающий трансляционной симметрией?
   
   Это тип симметрии, при котором при сдвиге объекта на определенный вектор (вектор трансляции) получается идентичный объект.
   
   Идеализация – кристалл.
   <Бесконечный в направлении вектора трансляции объект с периодичной (в том же направлении) внутренней структурой.>
   
3. Что такое кристалл?
   
   Молекулярный кристалл – это много экзепляров молекулы, расположенных регулярным образом. В общем случае, кристаллы это твердые тела, частицы которых образуют трёхмерно-периодическую пространственную укладку.
   Структура кристалла определяется тремя векторами трансляции.
   
   Кристалл – это структура, переходящая в саму себя при трансляционных симметриях на три некомпланарных вектора.
   

4. Что такое кристаллографическая ячейка? Иногда говорят “элементарная ячейка кристалла”.
   

   Параллелепипед, построенный по трем векторам трансляции, такой что сдвиги на эти векторы являются симметриями кристалла и его нельзя уменьшить, сохранив первое свойство.
   
   Элементарная ячейка – математический объект. Она вводится для удобства работы.

5. Что такое кристаллографическая симметрия? Что такое нетрансляционная симметрия кристалла? Привести пример для плоского кристалла.
   
   Это симметрия, которая распространяется на весь кристалл.
   
   <Нетрансляционная симметрия – все типы симметрий, кроме трансляционной.
   Поворотная ось 2, 3, 4 или 6 порядка, а также зеркальная симметрия.>
   
6. Что такое кристаллографическая группа, обозначение которой приводится в PDB файле?
   
   Это группа симметрии (т. е. способ комбинирования элементов симметрии) для данного кристалла.
   Это набор всех симметрий кристалла.
   
7. Что такое асимметрическая ячейка кристалла?
   
   Это наименьшая часть структуры кристалла, применение к которой операторов симметрии позволит получить элементарную ячейку.
   
   
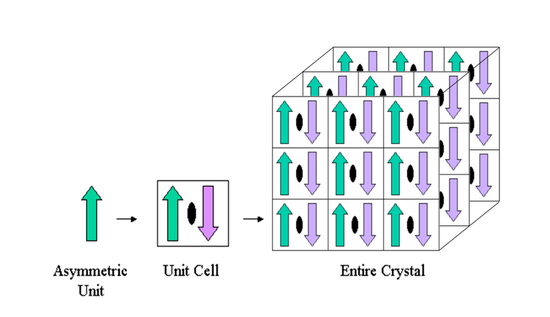
8. Какие данные содержатся в PDB файле для восстановления молекул из соседних асимметрических ячеек кристалла?
   
   Операторы симметрии. Поле «SYMMETRY OPERATORS FOR SPACE GROUP...». Матрицы для абсолютных координат – «SMTRY#».
   
9. Что такое некристаллографическая симметрия (молекулы или комплекса молекул в кристалле)?
   
   Это симметрия, которая не распространяется на весь кристалл и имеет место лишь в ограниченной области пространства.
   
   Пример:
   
   

10. Какими свойствами обладает функция электронной плотности кристалла?
    
    rho(r) = rho(r+a)
rho(r) = rho(r+b)
rho(r) = rho(r+c)

Ряд Фурье

1. Что такое ряд Фурье периодической функции? Напишите формулу для n-го слагаемого ряда. Что такое гармоника и какими параметрами она определяется? На примере функций одной переменной.
   
   Это представление периодической функции в виде бесконечной суммы («комбинации косинусов и синусов»).
   
   
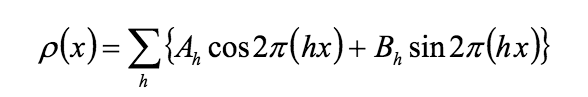
   Ряд, слагаемые которого являются синусоидами с периодом, равным T/n, где T – длина заданного отрезка, n - целое положительное число. Слагаемое называется гармоникой, отвечающей номеру n. Кроме номера, у гармоники два параметра:
   - амплитуда – неотрицательное число, равное максимуму синусоиды;
   - фаза, равная сдвигу синусоиды вдоль оси x.

   
   Первое слагаемое ряда имеет номер 0 и является константой.

   Сумма ряда Фурье является периодической функцией с периодом T. В трехмерном случае номер гармоники задается тремя целыми неотрицательными числами h, k, l.
   

2. Даны параметры некоторого набора гармоник ряда Фурье. Как восстанавливается функция по этому набору? (Такое восстановление называется также синтезом Фурье.)
   
   
   
   
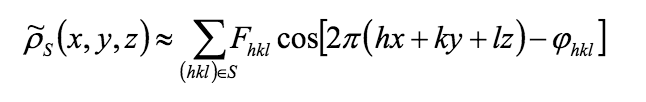
3. Что такое полный набор гармоник? Что такое разрешение полного набора гармоник? Как связано качество восстановления функции и разрешение набора гармоник?
   
   Набор гармоник ряда Фурье называется полным, если известны все гармоники с номерами 0, 1, 2, ..., n.
   
   Разрешением полного набора гармоник называется период гармоники с номером n, т.е. с наибольшим номером. Период гармоники равен расстоянию между соседними максимумами синусоиды; его также называют длиной волны этой гармоники, хотя никакой физической волны нет.
   
   Если разрешение полного набора гармоник равно d (ангстрем), то на восстановленной функции неразличимы детали размера меньше чем d/2, имеющиеся на графике исходной функции.
   
4. Что такое неполный набор гармоник? Как определяется его разрешение и что такое полнота данных для данного разрешения?
   
   Набор, в который входят не все гармоники с разрешением большим или равным d.
   
   Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо сообщить полноту данных — процент гармоник с длиной волны не меньшей d от максимально возможного, присутствующих в наборе. Для полного набора данных (разрешение d=T/n) полнота равна 100%.
   
5. Напишите ряд Фурье для функции электронной плотности кристалла.
   
   
   

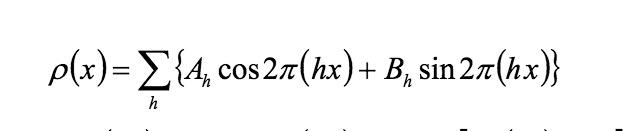
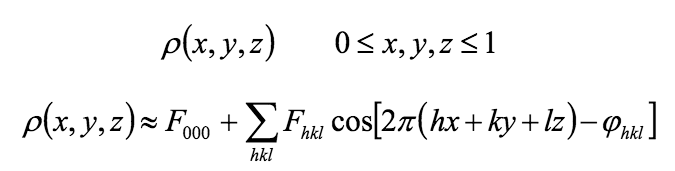
Теория рассеяния

1. Что такое абсолютные и относительные координаты? Как связаны относительные координаты с параметрами кристаллографической ячейки?
   
   Это различные координаты для элементарной ячейки кристалла. В относительных координатах (x, y, z) длины векторов a, b и с равны 1. r = x*a + y*b + z*c
   
   
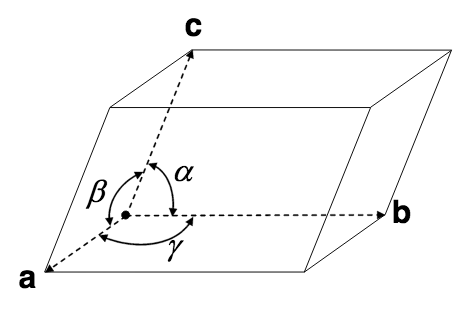
   Система абсолютных координат (X, Y, Z) ортогональная. Единица измерения - ангстрем.
   
   
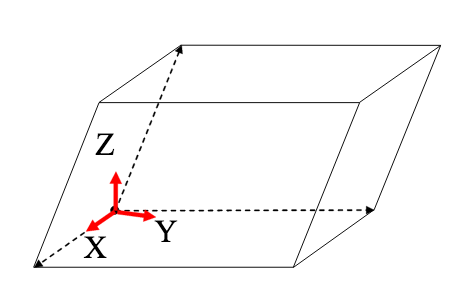
   В файлах .pdb обычно записаны абсолютные координаты. Для перехода в относительные есть поле SCALE.
   
2. Что такое вектор рассеяния? Как найти вектор рассеяния для данного направления на детектируемый сигнал?
   
   Вектор рассения s:
   
   
   
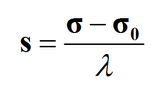
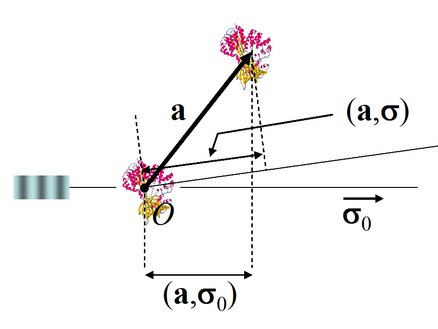
3. Сформулируйте условия Лауэ (на направления, в которых наблюдается дифракция на кристалле).
   
   
   
4. Что такое рефлекс? Как связаны индексы рефлекса h, k, l и соответствующий им вектор рассеяния s?
   
   Рефлекс – это сигнал, улавливаемый детектором (“черное пятнышко” если детектор – фотопластинка). Расположение рефлексов на детекторе позволяет определить параметры кристаллографической ячейки и все кристаллографические симметрии.
   
   Направление из кристалла на точку детектора однозначно определяет вектор рассеяния s. Сигнал в данном направлении усиливается только тогда, когда скалярные произведения вектора рассеяния с векторами a, b, c кристаллографической ячейки равны целым числам. Это и есть числа h, k, l рефлекса.
   
5. Какая величина измеряется в эксперименте?
   
   Интенсивность, значение которой примерно равно квадрату модуля структурного фактора.
   
6. По каким данным эксперимента определяются параметры кристаллографической ячейки?
   
   Расположение рефлексов на детекторе позволяет определить параметры кристаллографической ячейки и все кристаллографические симметрии.
   
7. Как связаны величины, измеренные в эксперименте, с разложением функции электронной плотности кристалла в ряд Фурье? На основании чего устанавливается эта связь?
   
   Из теории рассеяния следует, что интенсивность излучения, детектируемого в направлении, характеризующемся целыми числами h, k, l, пропорциональна квадрату амплитуды гармоники с номером h, k, l. Связь устанавливается так: формулы, выведенные физиками для корня из интенсивности рефлекса h, k, l, совпадают с формулами для вычисления амплитуды гармоники h, k, l.
   ?
   
8. Напишите формулу для синтеза Фурье электронной плотности кристалла и объясните смысл использованных обозначений.
   
   
   
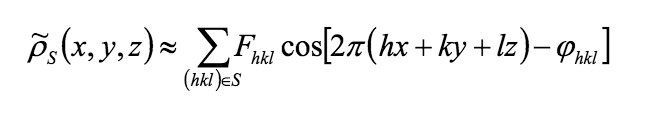
9. Напишите формулу для одной гармоники Фурье, выражающую зависимость одной гармоники Фурье от вектора r=(x,y,z) (из начала координат в данную точку).
   
   
   
   
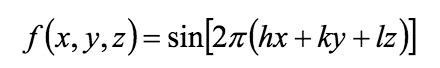
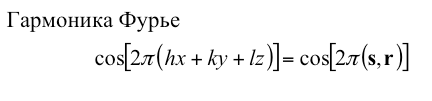
10. Что такое разрешение гармоники Фурье в одномерном и трехмерном случаях?
    
    Каждая гармоника Фурье имеет разрешение. В одномерном случае разрешением называется период синусоиды. В трехмерном случае гармоника h, k, l изменяется как синусоида вдоль одной прямой и постоянна на перпендикулярной плоскости. Естественно, разрешением называется период синусоиды.
    

11. Дан набор измеренных в эксперименте модулей структурных факторов. (“модуль структурного фактора h, k, l” и “амплитуда гармоники Фурье h, k, l” – одно и то же). Как определить разрешение структуры?
    
    

Фазовая проблема

1. В чём состоит фазовая проблема?
   
   В одном рентгеновском эксперименте с постоянной длиной волны рентгеновского излучения нельзя непосредственно измерить фазу структурных факторов, которые необходимы для обратного преобразования Фурье и определения электронной плотности.
   
2. Перечислите основные методы решения фазовой проблемы.
   
   Методы молекулярного замещения, изоморфного замещения и аномального рассеяния.
   
   
   

3. Метод изоморфного замещения: какие дополнительные эксперименты требуется провести?
   
   Кроме исходного кристалла, нужно получить еще два кристалла, полученные из исходного добавлением разных тяжелых атомов - используют ртуть, платину, золото и др. Такие кристаллы можно получить экспериментально добавлением к существующему соответствующих атомов. Они называются изоморфным замещением исходного кристалла.

   Если белки в обоих кристаллах, полученных изоморфным замещением, сохраними свое расположение, и атомы тяжелого металла присоединились во всех кристаллограических ячейках в одном и том же месте, то можно провести еще два рентгеновских эксперимента и по результатам трех рентгеновских экспериментов (исходный кристалл белка, изоморфное замещение одним тяжелым атомом, изоморфное замещение другим тяжелым атомом) решить фазовую проблему.
   

4. Что требуется для применения метода аномального рассеяния?
   
   Бывает достаточно ОДНОГО кристалла белка, в который внедрены тяжелые атомы, аномально рассеивающие рентгеновское излучение. Аномально - значит, что для них применяемая для белков теория рассеяния неточна. По несоответствию рефлексов теории можно решить фазовую проблему ПРИ УСЛОВИИ:

   для кристалла (с аномально рассеивающими атомами) получены результаты рентгеновского эксперимента с ТРЕМЯ разными длинами рентгеновских волн.

   Практически, используют белок с селенометионинами (селен - аномально рассеивающий атом; MSE в .pdb) и синхротрон, позволяющий проводить эксперименты с рентгеновскими волнами разных длин.
   

5. Опишите этапы решения фазовой проблемы методом молекулярного замещения.
   
   Нужна пространственная структура белка, похожего по структуре на исследуемый белок. Например,

   структура того же белка с другим лигандом;

   структура того же белка, решенная методом ЯМР;

   иногда даже структура того же белка, построенная методами теоретического моделирования;

   структура другого белка - гомолога данного; гомология может быть установлена по сходству последовательностей.
   
   
   

6. Комбинированный синтез Фурье (в методе молекулярного замещения).
   
   

Оптимизация модели

1. Как проводится оптимизация структуры? R-фактор. Составной R-фактор.
   
   Минимизация величины R-фактора:
   
   
   
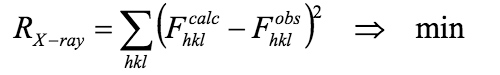
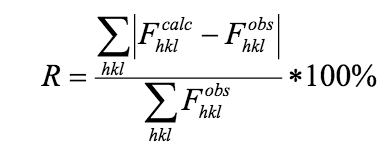
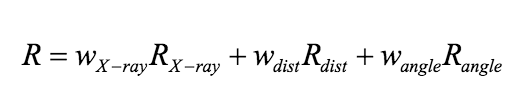
   Составной R-фактор учитывает стереохимические ограничения.
   
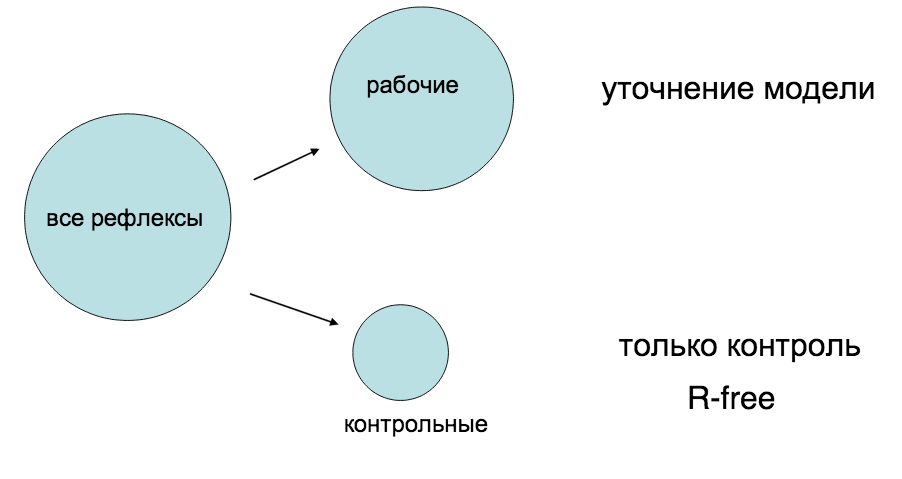
2. Свободный R-фактор (R_free): как считается, зачем нужен.
   
   Разделяем рефлексы на рабочие, по которым строится модель и вычисляет R-фактор, и контрольные, для которых по той же формуле вычисляет Rfree. Как правило, в хорошей структуре полученные значения различаются на 5%. Позволяет обнаружить «подгонку» (overfitting).
   
   

Индексы качества модели

1. Что такое температурный фактор (B-фактор)?
   
   То же, что и ADP – atomic displacement parameter. Атом может колебаться или быть по-разному расположенным в разных ячейках. Характеризует дисперсию – размазанность пика вокруг атома. Измеряется в квадратных ангстремах.
   
2. Что такое коэффициент заполнения атома и почему он не всегда равен 1?
   
   Это показатель того, какой процент элементарных ячеек содержит атом в указанной позиции.
   
   Например, молекулы воды в определенной позиции могут отсутствовать в ряде ячеек. Остаток может иметь несколько альтернативных конформаций.
   
3. Перечислите основные показатели качества рентгеноструктурной модели.
   
   Rfree и Rfree-R;
   карта Рамачандрана;
   комфортность окружения атомов (packing score);
   разрешение, ротамеры, RSR;
   сравнение копий из асимметрической единицы, инверсия пептидной цепи между двумя Calpha (pep-flip);
   B-factor, геометрические показатели, R-factor.
   
4. Индикаторы качества модели в целом (перечислить; что отражают).
   
   R-factor, Rfree и Rfree-R;
   карта Рамачандрана (степени свободы полипептидной цепи);
   комфортность окружения атомов (packing score).
   
   ...
   
5. Карта Рамачандрана и её использование для оценки качества модели.
   
   Для остатков структуры можно построить карту. Есть классификация областей (PROCHECK): предпочитаемая, разрешённая, допустимая и запрещённая.
   Остатки, не попадающие в обведённые области на карте, следует считать маргинальными. Области определены на основании статистики по PDB.
   
   В хорошей модели >90% остатков, не считая Gly и Pro, находятся в предпочитаемой области.
   
6. Как по модели и модулям структурных факторов вычисляется "экспериментальная" электронная плотность (для визуализации и оценки моделирования отдельных остатков).
   
   По модели рассчитываются фазы.
   Затем применяют комбинированный синтез Фурье (см. вопрос 37) для вычисления функции электронной плотности.
   
7. Индикаторы маргинальных остатков в модели (перечислить, что отражают).
   
   Маргинальные остатки: либо координаты остовных атомов существенно не точны, либо это крайне редкие особенности, требующие объяснения.
   
   См. вопросы 44, и 47, и 48, и 49, и 50.
   
8. Пространственный R-фактор.
   
   RSR (real-space R-factor) характеризует то, насколько модель группы атомов (или отдельного атома) соответствует экспериментальной электронной плотности.
   
   (См. вопрос 45.)
   
   Для маргиналов с RSR>20% имеет смысл посмотреть, как остаток вписан в электронную плотность.
   
9. Как вычисляется Z-score пространственного R-фактора?
   
   Как нормированное отклонение наблюдаемого значения RSR от ожидаемого:
   
   
   Высокие положительные значения (Z > 2) свидетельствуют о том, что остаток плохо вписан в электронную плотность по сравнению с другими структурами с тем же разрешением. Этот остаток – маргинал.
   
10. Ротамеры боковых цепей (что такое, как используются).
    
    Ротамеры – это боковые цепи в типичных для данного типа остатка конформациях.
    Имеются базы данных ротамеров.
    Боковые цепи, конформация которых существенно отличается от одной из предпочитаемых, считаются маргинальными.
    
11. Комфортность окружения атома (в чем состоит, как используется).
    
    Невозможны пересечения ван-дер-Ваальсовских радиусов атомов. Заряд остатка должен компенсироваться взаимодействием с зарядом противоположного знака. Донорам/акцепторам протона выгодно образовывать водородную связь (если её нет, то остаток – маргинал). Неполярным атомам предпочтительно находиться в гидрофобном окружении.
    
    Используют интегральную оценку комфортности окружения остатка, в программе WhatCheck рассчитывается Z-score. Маргиналы – с Z-score < -5.
    

12. Молекулы воды в PDB файле (при каких условиях могут быть определены, как выявить ошибочно присутствующие в файле).
    
    Могут быть определены, если «зафиксированы» водородными связями. Если же расстояние велико, то эта молекула не может быть зафиксирована в одинаковых точках во всех ячейках кристалла.

ЯМР

1. Что такое ядерный магнитный резонанс (ЯМР) и как он может быть применён к исследованию структур молекул?
   
   Это физический феномен, суть которого состоит в том, что ядра в магнитном поле поглащают электромагнитное излучение и испускают его.
   
   
   

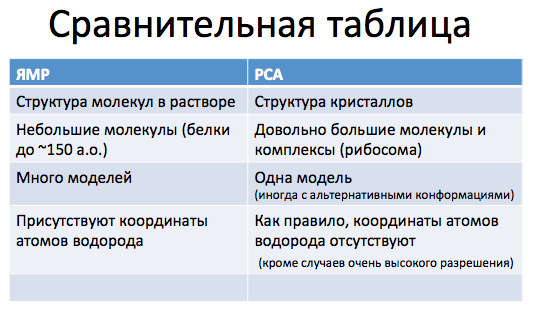
2. Особенности записей PDB, полученных методом ЯМР.
   
   

Содержание записей PDB, полученных методом рентгеновской кристаллографии

% HEADER: classificatin, deposition date, idCode

HEADER GENE REGULATION 28-SEP-05 2B5A

REMARK 2 RESOLUTION. 1.54 ANGSTROMS.

REMARK 3 DATA USED IN REFINEMENT.

REMARK 3 RESOLUTION RANGE HIGH (ANGSTROMS) : 1.54

REMARK 3 RESOLUTION RANGE LOW (ANGSTROMS) : 19.74

REMARK 3 DATA CUTOFF (SIGMA(F)) : 0.000

REMARK 3 COMPLETENESS FOR RANGE (%) : 99.5

REMARK 3 NUMBER OF REFLECTIONS : 44881

REMARK 3 R VALUE (WORKING + TEST SET) : 0.167

REMARK 3 R VALUE (WORKING SET) : 0.165

REMARK 3 FREE R VALUE : 0.201

REMARK 3 FREE R VALUE TEST SET SIZE (%) : 5.033

REMARK 3 FREE R VALUE TEST SET COUNT : 2259

REMARK 290 CRYSTALLOGRAPHIC SYMMETRY TRANSFORMATIONS

REMARK 290 THE FOLLOWING TRANSFORMATIONS OPERATE ON THE ATOM/HETATM

REMARK 290 RECORDS IN THIS ENTRY TO PRODUCE CRYSTALLOGRAPHICALLY

REMARK 290 RELATED MOLECULES.

REMARK 290 SMTRY1 1 1.000000 0.000000 0.000000 0.00000

REMARK 290 SMTRY2 1 0.000000 1.000000 0.000000 0.00000

REMARK 290 SMTRY3 1 0.000000 0.000000 1.000000 0.00000

%ATOM: serial №, name, resn, chain ID, resi, X, Y, Z (Angstroms), occupancy, temperature factor

ATOM 2472 OE2 GLU D 76 7.580 19.345 59.759 1.00 76.28

HETATM 2479 O ACY D 78 18.434 7.347 46.387 1.00 21.28

% CRYST1: a, b and c (Angstroms), alpha, beta, gamma (degrees), space group, Z-value (the number of polymeric chains in a unit cell)

CRYST1 63.205 65.016 73.296 90.00 90.00 90.00 P 21 21 2 16