Восстановление электронной плотности (ЭП)
1. Задание функции
Для проведения компьютерного эксперимента была использована следующая модель: На отрезке [0,30] (ангстремы) расположены две молекулы. Первая молекула содержит три атома, вторая-два. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Всего 3 различных типа атомов. Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.
Функция, описывающая данную модель, была создана с помощью скрипта . Гауссова функция определяется числами lambda,beta,gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2). Здесь a^2=a*a. Использованная команда:
python compile-func.py -o outfuncc.txt -g 30,3.3,5+20,3,6.3+30,3.3,7.6+25,3,12+30,3,13.4
Результат работы скрипта представлен в файле, а график функции на рисунке ниже.
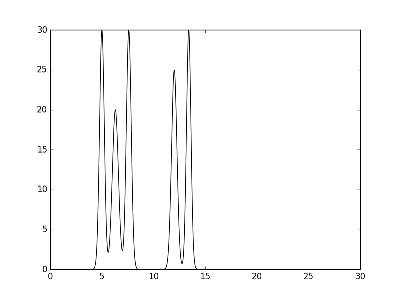
Рис.1. График электронной плотности одномерной модели двух молекул.
2. Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные
Затем с помощью скрипта функция была разложена в ряд Фурье. Было получено 500 гармоник (0-499), их коэффициенты (фазы и амплитуды) записаны в файл.
3. Восстановление функции ЭП по амплитудам и фазам части сигналов
Полные наборы гармоник
По различным полным наборам гармоник с помощью скрипта восстанавливалась исходная функция распределения ЭП. . Их наложение на исходную функцию показано на рисунке 2.
 <
<
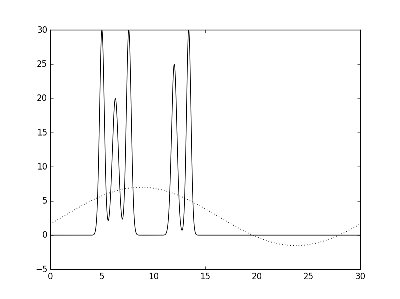
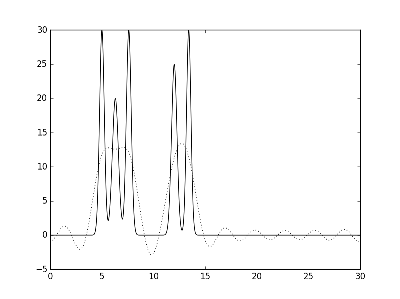
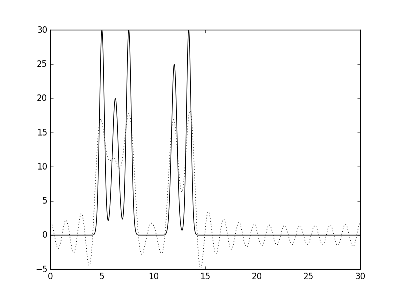
Рис.2. Графики электронной плотности одномерной модели двух молекул и её восстановление с помощью различных полных наборов гармоник. Слева направо и сверху вниз использовались наборы гармоник: с 0 по 1, с 0 по 10, с 0 по 20 и с 0 по 30.
Как видно из рисунка, набор с 0 по 30 является минимальным полным набором гармоник, при котором восстановление функции можно считать отличным
Полный набор гармоник с 0 по 30 при различных уровнях шума
Скрипт func2fourier также позволяет добавлять шум в амплитуды (F) и фазы (P). Шум 20% означает, что к каждому значению Х прибавляется случайное число, распределенное нормально с параметрами: среднее = 0, среднее квадратичное отклонение (сигма)=0.2*Х. Ниже представлены результаты восстанвления по полному набору гармоник с 0 по 30 при различных уровнях шума.
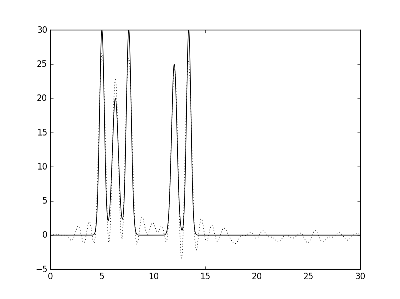
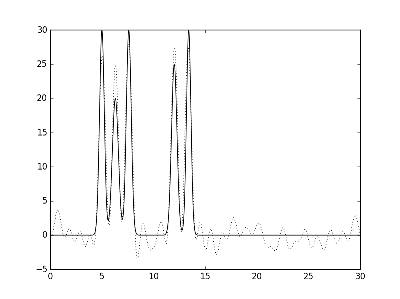
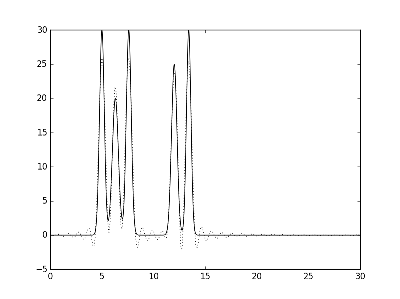
Рис.2. Графики электронной плотности одномерной модели двух молекул и её восстановление с помощью полного набора гармоник с 0 по 30. Слева направо представлено восстановление при различных уровнях шума амплитуды: f 10% и f 20%.
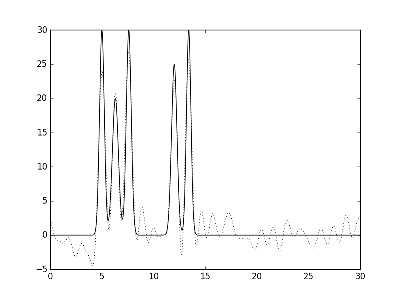
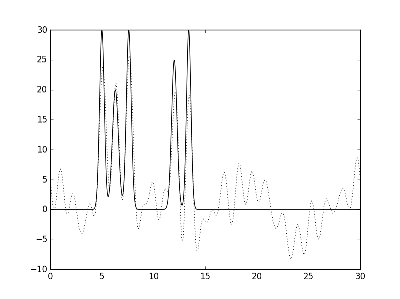
Рис.3. Графики электронной плотности одномерной модели двух молекул и её восстановление с помощью полного набора гармоник с 0 по 30. Слева направо представлено восстановление при различных уровнях шума фазы: p 10% и p 20%.
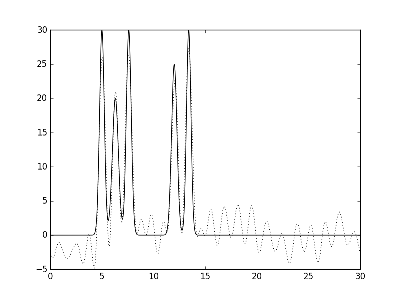
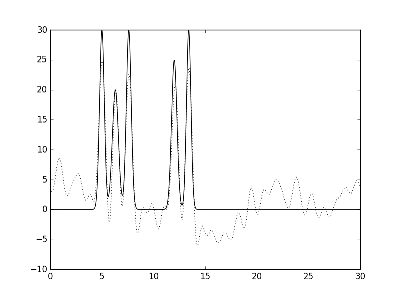
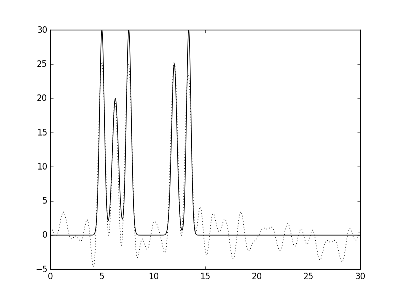
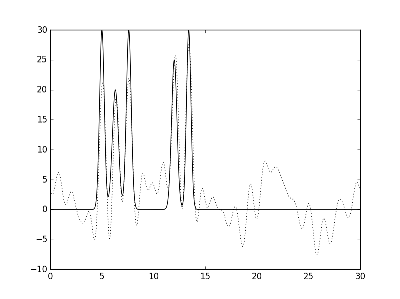
Рис.4. Графики электронной плотности одномерной модели двух молекул и её восстановление с помощью полного набора гармоник с 0 по 30. Слева направо и сверху вниз представлено восстановление при различных уровнях шума амплитуды и фазы: f 10% p 10%, f 10% p 20%, f 20% p 10% и f 20% p 20 %.
Неполные наборы гармоник
Аналочичным образом была восстановлена функция ЭП при использовании различных неполных наборов гармоник.

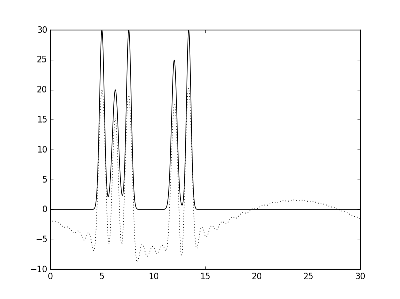
Рис.5. Графики электронной плотности одномерной модели двух молекул и её восстановление с помощью различных неполнох наборов гармоник. Слева направо представлено восстановление при различных наборах гармоник: с 1 по 30 и со 2 по 30.
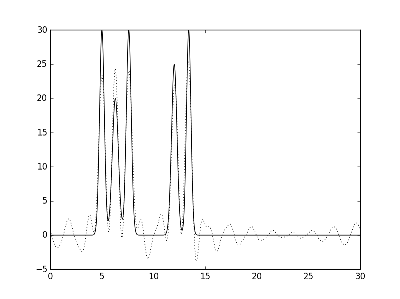
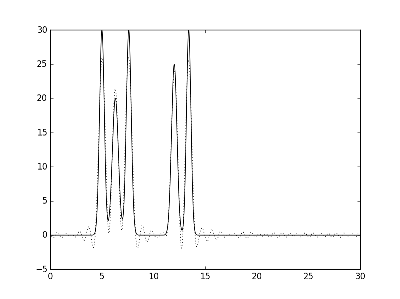
Рис.6. Графики электронной плотности одномерной модели двух молекул и её восстановление с помощью различных неполнох наборов гармоник. Слева направо представлено восстановление при различных наборах гармоник: с 0 по 30, но без 13 и 14 и с 0 по 30, включая 40.
4. Расчет разрешения
Результаты эксперимента собраны в таблице ниже.
| Набор гармоник | Разрешение | Полнота данных | Шум амплитуды (% от величины F) | Шум фазы | Качество восстановления | Комментарии |
| (Å) | (%) | (% от величины phi) | (отличное, хорошее, среднее, плохое) | |||
| Полный набор гармоник | ||||||
| 0–1 | 30 Å | 100% | 0 | 0 | Плохое | |
| 0–10 | 3 Å | 100% | 0 | 0 | Среднее | |
| 0–20 | 1,5 Å | 100% | 0 | 0 | Хорошее | Пик второго атома слабо различим |
| 0-30 | 1 Å | 100% | 0 | 0 | Отличное | |
| 0-30 | 1 Å | 100% | 10 | 0 | Отличное | |
| 0-30 | 1 Å | 100% | 20 | 0 | Отличное | |
| 0-30 | 1 Å | 100% | 0 | 10 | Отличное | |
| 0-30 | 1 Å | 100% | 0 | 20 | Отличное | |
| 0-30 | 1 Å | 100% | 10 | 10 | Отличное | |
| 0-30 | 1 Å | 100% | 20 | 20 | Хорошее | |
| 0-30 | 1 Å | 100% | 10 | 20 | Хорошее | Почти отличное |
| 0-30 | 1 Å | 100% | 20 | 10 | Отличное | |
| Неполный набор гармоник | ||||||
| 1–30 | 96.8% | 0 | 0 | Отличное | ||
| фев.30 | 93.5% | 0 | 0 | Отличное | ||
| 0-12,15-30 | 93.5% | 0 | 0 | Отличное | ||
| 0-30, 40 | 100% | 0 | 0 | Отличное | ||