Работали с программами пакета EMBOSS:
I. Матрица переходов
a) Глобальное выравнивание
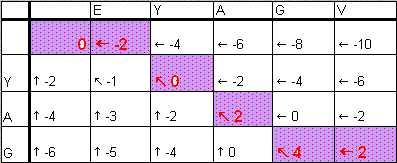
матрица переходов глобального выравнивания строилась для последовательностей EYAGV и YAG
при построении вес совпадения брался 2, вес замены -1, штраф за дилецию -2

выравнивание,соответствующее оптимальному пути:
sq1: EYAGV sq2: -YAG-
a) Локальное выравнивание
наименнее удачное с весом 4
sq1: KPVTLYDVA sq2: PV
оптимальное с весом 6
sq1: KPVTLYDVA
sq2: DVA
II. Поиск участков локальной гомологии
Эта часть посвящена анализу результатов, полученных с помощью программы построения локального выравнивания matcher
матрица переходов глобального выравнивания строилась для последовательностей MKPVTLYDVAEYAGVSYQTVSRVVNQASHVSAKTREKVEAAMAELNYIPNRVAQQLAGKQSLLIGVATSSLALHAPSQIVAAIKSRADQLGASVVVSMVERSGVEACKAAVHN LLAQRVSGLIINYPLDDQDAIAVEAACTNVPALFLDVSDQTPINSIIFSHEDGTRLGVEHLVALGHQQIALLAGPLSSVSARLRLAGWHKYLTRNQIQPIAEREGDWSAMSGFQ QTMQMLNEGIVPTAMLVANDQMALGAMRAITESGLRVGADISVVGYDDTEDSSCYIPPLTTIKQDFRLLGQTSVDRLLQLSQGQAVKGNQLLPVSLVKRKTTLAPNTQTASPR ALADSLMQLARQVSRLESGQ и LYDVAEYAGVADSLMQLARQ
вторая последовательность была составлена из участков 6-15 и 343-352 (включительно) первой последовательности
10
P03023: LYDVAEYAGVS
::::::::::.
seq3: LYDVAEYAGVA
10
350
P03023: LADSLMQLARQ
.::::::::::
seq3: VADSLMQLARQ
10 20
III. Влияние параметров на глобальное выравнивание
параметры выравнивания:
|
|
P03023 1 MKPVTLYDVAEYAGVSYQTVSRVVNQASHVSAKTREKVEAAMAELNYIPN 50
||||||||||: .::.::..|
seq3 1 LYDVAEYAGVA-DSLMQLARQ 20
P03023 51 RVAQQLAGKQSLLIGVATSSLALHAPSQIVAAIKSRADQLGASVVVSMVE 100
seq3 21 20
P03023 101 RSGVEACKAAVHNLLAQRVSGLIINYPLDDQDAIAVEAACTNVPALFLDV 150
seq3 21 20
P03023 151 SDQTPINSIIFSHEDGTRLGVEHLVALGHQQIALLAGPLSSVSARLRLAG 200
seq3 21 20
P03023 201 WHKYLTRNQIQPIAEREGDWSAMSGFQQTMQMLNEGIVPTAMLVANDQMA 250
seq3 21 20
P03023 251 LGAMRAITESGLRVGADISVVGYDDTEDSSCYIPPLTTIKQDFRLLGQTS 300
seq3 21 20
P03023 301 VDRLLQLSQGQAVKGNQLLPVSLVKRKTTLAPNTQTASPRALADSLMQLA 350
seq3 21 20
P03023 351 RQVSRLESGQ 360
seq3 21 20
|
P03023 1 MKPVTLYDVAEYAGV--SY-QTVSRVVNQASHVSAKTREKVEAAMAELNY 47
|||||||||| |. | ::| |
seq3 1 LYDVAEYAGVADSLMQ-LAR---Q 20
P03023 48 IPNRVAQQLAGKQSLLIGVATSSLALHAPSQIVAAIKSRADQLGASVVVS 97
seq3 21 20
P03023 98 MVERSGVEACKAAVHNLLAQRVSGLIINYPLDDQDAIAVEAACTNVPALF 147
seq3 21 20
P03023 148 LDVSDQTPINSIIFSHEDGTRLGVEHLVALGHQQIALLAGPLSSVSARLR 197
seq3 21 20
P03023 198 LAGWHKYLTRNQIQPIAEREGDWSAMSGFQQTMQMLNEGIVPTAMLVAND 247
seq3 21 20
P03023 248 QMALGAMRAITESGLRVGADISVVGYDDTEDSSCYIPPLTTIKQDFRLLG 297
seq3 21 20
P03023 298 QTSVDRLLQLSQGQAVKGNQLLPVSLVKRKTTLAPNTQTASPRALADSLM 347
seq3 21 20
P03023 348 QLARQVSRLESGQ 360
seq3 21 20
|
| score:50 |
score:111 |
с уменьшением GO повышается частота одиночных гэпов(при GO=1=GP мы не учитываем что остатки обычно мутируют группами) и вес выравнивания увеличится,
при изменении матрицы происходит изменение цен замен и совпадений. в матрице 80 больше цена совпадения и меньше - несовпадения(т.к. она строится по двум последовательностямкоторые схожи на 80%),поэтому при переходе к большей матрице 80 вес по идее увеличивается,но так как все эти значения веса зависят от того ,по какой конкретно выборке строилась матрица перехода,то вообще трудно сказать наверняка как изменится вес при изменении матрицы,т.к. это зависит от выборок по которым строились матрицы переходов..
Blastp