Сборка генома de novo.
Чтения
На соответствующем сайте я скачала чтения (в формате fastq) проекта по секвенированию бактерии Buchnera aphidicola с данным мне кодом доступа - SRR4240359. Файл был перенесен в директорию /nfs/srv/databases/ngs/e.caterina/pr13 и там распакован:
| gunzip SRR4240359.fasrq.gz
Подготовка чтений
Для сборки генома требовалась предварительная подготовка чтений. Во-первых, необходимо было удалить остатки адапетров: их последовательности были скапированы из папки /P/y16/term3/block3/adapters в файл adapters.fa. Затем эти последовательности были удалены из ридов:
| java -jar /usr/share/java/trimmomatic.jar SE -phred33 SRR4240359.fastq SRR4240359_1.fastq ILLUMINACLIP:adapters.fa:2:7:7 Input Reads: 13557938 Surviving: 13502036 (99,59%) Dropped: 55902 (0,41%)Анализ чтений (SRR4240359.fastq):
| fastqc SRR4240359.fastqАнализ чтений (SRR4240359_1.fastq):
| fastqc SRR4240359_1.fastq
После этого были удалены буквы с плохим качеством и чтения, длиной менее 30 букв:
| java -jar /usr/share/java/trimmomatic.jar SE -phred33 SRR4240359_1.fastq SRR4240359_cl.fastq TRAILING:20 MINLEN:30 Input Reads: 13502036 Surviving: 12549379 (92,94%) Dropped: 952657 (7,06%)Анализ чтений (SRR4240359_cl.fastq):
| fastqc SRR4240359_cl.fastqРазмер файла изменился с 1375М (до удаления адаптеров) на 1369М (после удаления адаптеров) и 1256М после удаления плохих чтений (сколько ридов было выкинуто написано в выводе команд).
Сборка
Первый этап сборки - подготовка k-меров (k=29 и k=25). Она была выполнена с помощью команды velveth пакета velveth:
| velveth velveth 29 -fastq -short SRR4240359_cl.fastq | velveth velveth 25 -fastq -short SRR4240359_cl.fastq
Затем командой velvetg была произведена сама сборка:
| velvetg velveth Final graph has 2049 nodes and n50 of 47361, max 91528, total 723361, using 0/12549379 reads Final graph has 10154 nodes and n50 of 2982, max 17922, total 919878, using 0/12549379 readsЭта команда создала папку velveth и в ней следующие файлы:
Graph LastGraph Log PreGraph Roadmaps Sequences contigs.fa stats.txtПоследний содержит информация о покрытии и длине контигов (в k-мерах), причем в столбце *cov приведено покрытие с учетом немного отличающихся последовательностей, а в столбце *Ocov - только полностью совпадающих. Если назвать аномальными контиги, с покрытием больше чем в 5 раз больше среднего, то видно, что в первом случае ими оказываются первые два контига с максимальным покрытием, во втором - все три контига, в третьем - только первый контиг с максимальным покрытием.
Таблица 1. Покрытия, длины контигов; k=29 |
Таблица 2. Покрытия, длины контигов; k=25 |
Таблица 3. Покрытия, длины контигов при сборке |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сборка половины файла
Т. к. было известно число ридов после очистки, а также то, что в формате fastq каждый рид имеет 4 строки, половина файла была получена записью первых 25098760 строк в другой файл (и было проверено, что конец файлв случайно не обрезает информацию посреди рида). Далее были проделаны все те же операции:
| head -25098760 SRR4240359_cl.fastq > SRRhalf.fastq
| tail -4 SRRhalf.fastq @SRR4240359.6720197 6720197/1 ATTTGGTTATGCTACTAATGAAACTGAATTTTTCAT + IIIIIIIIIII4IIIIIIIII'IIIIIIIIIIII7I
| velveth velveth 29 -fastq -short SRRhalf.fastq
| velvetg velveth Final graph has 672 nodes and n50 of 52117, max 111442, total 678130, using 0/6274690 reads
Анализ полученной сборки можно увидеть в таблице 3 (выше). Среднее покрытие упало примерно в 6 раз, максимальные покрытия контигов также уменьшились, строк с минимальным покрытием стало гораздо меньше (что не отражено в таблице). Почему-то увеличилась максимальная длина контигов - возможно, это как-то связано с трудностью правильного разрешения повторов при наличии только половины ридов.
Анализ
С помощью megablast (порог Evalue 0.01, длина слова 24) были получены выравнивания для трех самых длинных контигов с хромосомой Buchnera aphidicola (GenBank/EMBL AC — CP009253 - это subject, т. е. координаты на ней s.start и s.end ). В таблице 4 представлены данные по выравниваниям:
| subject acc.ver | query cover | % identity | alignment length | mismatches | gap opens | q. start | q. end | s. start | s. end | evalue | bit score |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NODE_4_length_91528_cov_53.88 (total score 35764) | |||||||||||
| CP009253.1 | 66% | 74,083 | 9592 | 2123 | 296 | 51681 | 61122 | 398726 | 389348 | 0,0 | 3605 |
| 79,606 | 5031 | 868 | 109 | 46453 | 51436 | 403823 | 398904 | 0,0 | 3461 | ||
| 79,528 | 4665 | 817 | 109 | 32299 | 36893 | 417677 | 413081 | 0 | 3197 | ||
| 80,255 | 3054 | 542 | 52 | 3379 | 6406 | 445895 | 442877 | 0 | 2242 | ||
| 77,106 | 3870 | 747 | 105 | 40098 | 43910 | 410208 | 406421 | 0 | 2109 | ||
| 76,199 | 4151 | 837 | 116 | 20326 | 24404 | 429483 | 425412 | 0 | 2052 | ||
| 82,361 | 2177 | 368 | 15 | 44042 | 46210 | 406218 | 404050 | 0 | 1879 | ||
| 77,082 | 2954 | 566 | 86 | 11310 | 14233 | 438139 | 435267 | 0 | 1602 | ||
| 77,343 | 2785 | 552 | 66 | 81975 | 84741 | 369544 | 366821 | 0 | 1574 | ||
| 75,186 | 3494 | 712 | 120 | 14295 | 17724 | 435241 | 431839 | 0 | 1506 | ||
| 82,042 | 1743 | 290 | 21 | 75484 | 77214 | 375867 | 374136 | 0 | 1463 | ||
| 80,799 | 1828 | 320 | 28 | 37980 | 39794 | 412321 | 410512 | 0 | 1402 | ||
| 80,937 | 1516 | 268 | 18 | 67774 | 69280 | 383115 | 381612 | 0 | 1179 | ||
| 79,044 | 1694 | 326 | 24 | 6536 | 8211 | 442817 | 441135 | 0 | 1134 | ||
| 78,823 | 1478 | 288 | 22 | 63845 | 65312 | 386887 | 385425 | 0 | 972 | ||
| 78,922 | 1243 | 239 | 19 | 62541 | 63769 | 388123 | 386890 | 0 | 822 | ||
| 76,896 | 1398 | 301 | 18 | 24505 | 25895 | 425347 | 423965 | 0 | 773 | ||
| 76,508 | 1426 | 292 | 41 | 80328 | 81733 | 371148 | 369746 | 0 | 737 | ||
| 74,796 | 1714 | 363 | 56 | 72152 | 73836 | 378849 | 377176 | 0 | 708 | ||
| 77,129 | 1198 | 248 | 20 | 931 | 2118 | 449336 | 448155 | 0 | 671 | ||
| 79,113 | 857 | 170 | 7 | 28514 | 29367 | 421327 | 420477 | 2,06E-165 | 582 | ||
| 76,782 | 1038 | 220 | 20 | 88647 | 89672 | 362954 | 361926 | 2,69E-159 | 562 | ||
| 74,057 | 1299 | 262 | 52 | 65376 | 66659 | 385420 | 384182 | 2,81E-129 | 462 | ||
| 78,073 | 602 | 113 | 15 | 29526 | 30122 | 420364 | 419777 | 2,93E-099 | 363 | ||
| 88,947 | 190 | 13 | 6 | 8333 | 8514 | 440944 | 440755 | 1,11E-058 | 228 | ||
| 79,636 | 275 | 44 | 10 | 86626 | 86896 | 364968 | 364702 | 1,89E-046 | 187 | ||
| 97,561 | 82 | 1 | 1 | 8604 | 8685 | 440732 | 440652 | 5,37E-032 | 139 | ||
| 72,78 | 518 | 100 | 36 | 37177 | 37666 | 412936 | 412432 | 1,93E-031 | 137 | ||
| NODE_3_length_83127_cov_51.23 (total score 31975) | |||||||||||
| CP009253.1 | 74% | 75,730 | 8459 | 1773 | 211 | 63898 | 72248 | 333222 | 341508 | 0,0 | 3989 |
| 76.669 | 7428 | 1549 | 151 | 24568 | 31921 | 295935 | 303252 | 0.0 | 3947 | ||
| 75,881 | 8396 | 1596 | 322 | 2546 | 10767 | 275566 | 283706 | 0 | 3890 | ||
| 76,819 | 4370 | 887 | 99 | 38755 | 43066 | 307878 | 312179 | 0 | 2342 | ||
| 77,534 | 3423 | 670 | 73 | 15945 | 19311 | 288181 | 291560 | 0 | 1969 | ||
| 77,111 | 3351 | 678 | 82 | 43711 | 47019 | 312679 | 315982 | 0 | 1857 | ||
| 76,349 | 3391 | 680 | 94 | 74025 | 77364 | 343228 | 346547 | 0 | 1707 | ||
| 73,978 | 4304 | 944 | 140 | 50053 | 54266 | 318826 | 323043 | 0 | 1581 | ||
| 75,955 | 2828 | 571 | 85 | 58084 | 60853 | 327227 | 330003 | 0 | 1354 | ||
| 80,965 | 1534 | 280 | 10 | 22733 | 24259 | 294227 | 295755 | 0 | 1205 | ||
| 75,48 | 2606 | 541 | 71 | 80178 | 82752 | 349918 | 352456 | 0 | 1182 | ||
| 74,727 | 2568 | 497 | 107 | 1 | 2487 | 273055 | 275551 | 0 | 1007 | ||
| 75,134 | 2240 | 488 | 61 | 55586 | 57792 | 324747 | 326950 | 0 | 987 | ||
| 78,483 | 1450 | 297 | 14 | 78487 | 79929 | 348233 | 349674 | 0 | 935 | ||
| 77,795 | 1297 | 239 | 38 | 72607 | 73879 | 341781 | 343052 | 0 | 754 | ||
| 75,982 | 1349 | 297 | 25 | 12821 | 14155 | 285200 | 286535 | 0 | 671 | ||
| 80,161 | 872 | 165 | 8 | 19520 | 20387 | 291693 | 292560 | 0 | 645 | ||
| 82,667 | 675 | 115 | 2 | 61234 | 61907 | 330333 | 331006 | 6,7E-170 | 597 | ||
| 76,237 | 1132 | 223 | 37 | 11015 | 12124 | 283963 | 285070 | 3,16E-158 | 558 | ||
| 81,754 | 570 | 102 | 2 | 21300 | 21868 | 293424 | 293992 | 3,27E-133 | 475 | ||
| 76,541 | 503 | 109 | 8 | 54899 | 55396 | 324054 | 324552 | 2,14E-070 | 267 | ||
| 100 | 24 | 0 | 0 | 6253 | 6276 | 431457 | 431434 | 0,001 | 45,4 | ||
| NODE_1_length_78160_cov_57.46 (total score 26526) | |||||||||||
| CP009253.1 | 72% | 74,946 | 13008 | 2715 | 426 | 20126 | 32866 | 127825 | 140555 | 0,0 | 5465 |
| 77,804 | 8168 | 1549 | 191 | 45885 | 53969 | 153752 | 161738 | 0,0 | 4796 | ||
| 77,747 | 7536 | 1434 | 178 | 36505 | 43904 | 144368 | 151796 | 0 | 4401 | ||
| 79,589 | 4914 | 891 | 92 | 54174 | 59034 | 161898 | 166752 | 0 | 3415 | ||
| 76,216 | 6517 | 1391 | 138 | 59065 | 65508 | 166750 | 173180 | 0 | 3301 | ||
| 72,489 | 4740 | 1059 | 181 | 5418 | 10003 | 113290 | 117938 | 0 | 1303 | ||
| 83,736 | 1199 | 184 | 9 | 18868 | 20061 | 126623 | 127815 | 0 | 1123 | ||
| 77,025 | 1741 | 334 | 54 | 16888 | 18604 | 124604 | 126302 | 0 | 939 | ||
| 77,546 | 1247 | 260 | 16 | 15655 | 16889 | 123332 | 124570 | 0 | 734 | ||
| 76,007 | 1192 | 246 | 38 | 33552 | 34719 | 141477 | 142652 | 5,52E-165 | 580 | ||
| 75,28 | 1072 | 213 | 46 | 34957 | 36005 | 142826 | 143868 | 5,8E-130 | 464 | ||
Таблица 4. Выравнивания трех самых длинных контигов
Ниже (рис. 1-3) приведены карты выравниваний. Видно, что покрытия расположены линейно, но имеют разрывы. При этом контиг 4 имеет обратную ориентацию.
 Рисунок 1. NODE_4_length_91528_cov_53 | 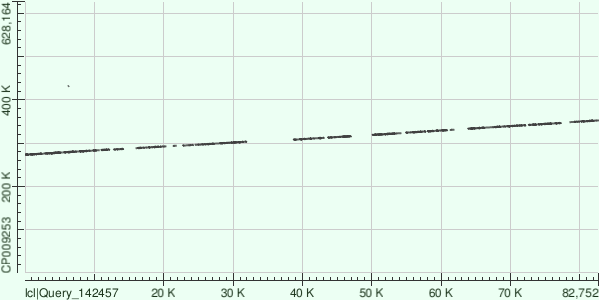 Рисунок 2.NODE_3_length_83127_cov_51 |  Рисунок 3.NODE_1_length_78160_cov_57.46 |
