Вернуться на страницу семестра
Цель работы: изучить качество восстановления функции ЭП от одной переменной
в зависимости от того, какие и сколько гармоник ряда Фурье используются для ее
восстановления.
Задание включает следующие этапы:
Создание модельной функции ЭП в одномерной элементарной ячейке
Расчет параметров сигнала, моделирующих экспериментальные данные: амплитуды и фазы
Восстановление функции ЭП по модельным ("экспериментальным") данным
Оценка качества восстановления функции ЭП
Этапы 3 - 4 предстоит повторить несколько раз.
1. Задание функции
Модель для компьютерного эксперимента. На отрезке [0,30] (ангстремы) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии
1-1.5 ангстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Всего 5-7 атомов
(2+3 или 2+3+2; возможны другие варианты). Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален
числу электронов в атоме.
Функция задается на интервале [0,30]. Моделируется в 1D график электронной плотности молекулы. 30 следует понимать как 30 ангстрем. Функция имеет вид нескольких
гауссовых кривых с центром в разных точках. Иногда - на расстоянии 1-1.5 ангстрем - модель ковалентно связанных атомов; иногда 3-5 ангстрем.
Задание функции:
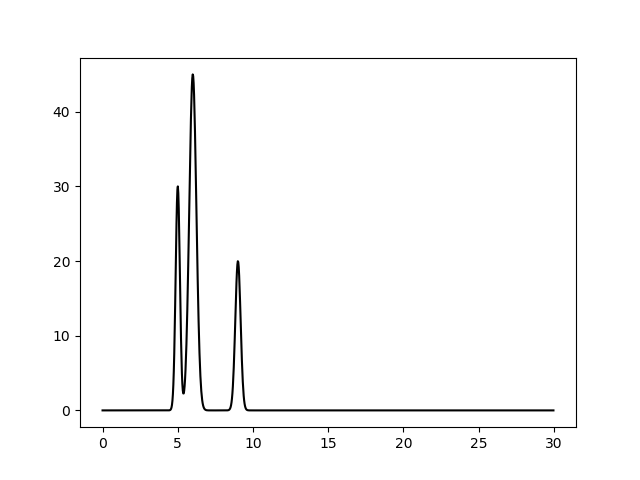
python2 compile-func.py -g 30,5,5+30,3,6+15,3,6+20,4,9 -o e_f.txt
Рисунок 1. Электронная плотность
2. Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные
Амплитуды и фазы рассчитываются по входной функции ЭП. При моделировании экспериментальных данных учитывается, что в эксперименте, во-первых, определяются амплитуды не для всех сигналов;
во-вторых, интенсивности сигналов (следовательно, и амплитуды) определяются с ошибкой; в-третьих, фазы определятся для всех измененных сигналов, но тоже с ошибкой.
Расчёт с шумом и без:
python2 func2fourier.py -i e_f.txt -o F_P_noise_fu_f.txt -F 15 -P 15
python2 func2fourier.py -i e_f.txt -o F_noise_fu_f.txt -F 15
python2 func2fourier.py -i e_f.txt -o fu_f.txt
Добавление гауссового шума к амплитудам (параметр -F <число>) и фазам (-P <число>) искажает все вычисленные амплитуды и фазы.
Пример: -F 20 (шум 20%) приводит к тому, что к каждой амплитуде прибавляется случайное число, распределенное нормально с параметрами:
среднее = 0, среднее квадратичное отклонение (сигма)=0.2*F. Аналогично действует параметр -P <число>
3. Восстановление функции ЭП по амплитудам и фазам части сигналов
Команды выбора нужных гармоник и восстановления:
python2 fourier-filter.py -i fu_f.txt -r 0-5 -o fu_f_cut_0-5.txt
python fourier2func.py -f e_f.txt -i fu_f_cut_0-5.txt -o fu_fu_0-5.txt
| | | | | | | | | | | |
| Полный набор гармоник, без шума |
| 0–10 | 0-20 | 0-30 | 0-40 |
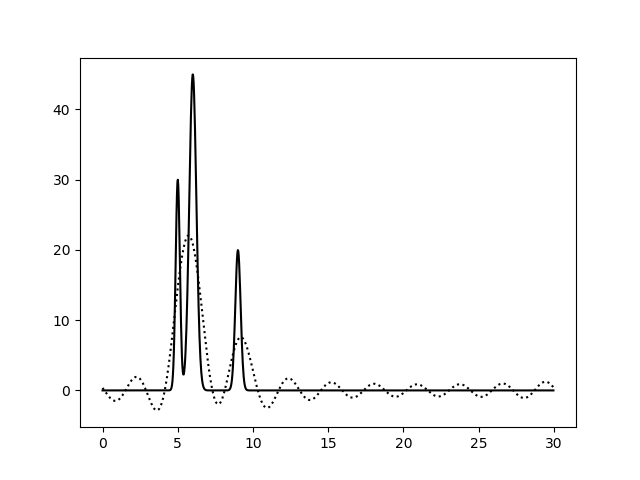 | 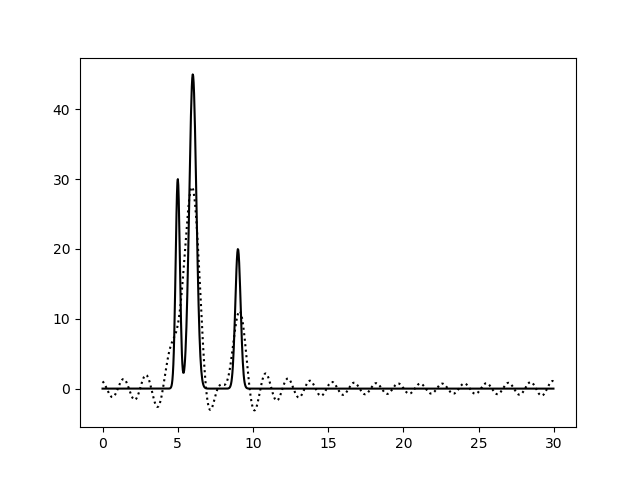 | 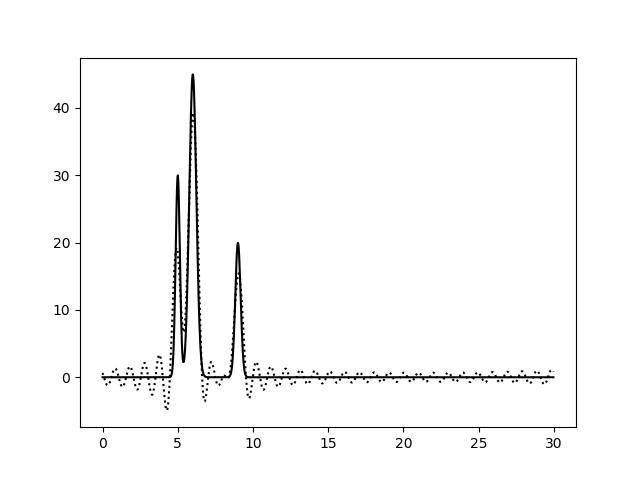 | 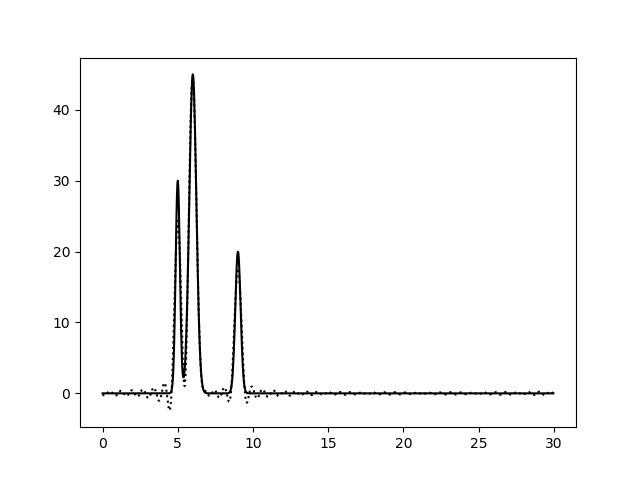 |
| Полный набор гармоник, с шумом (15% к амплитуде) |
| 0–10 | 0-30 | 0-40 |
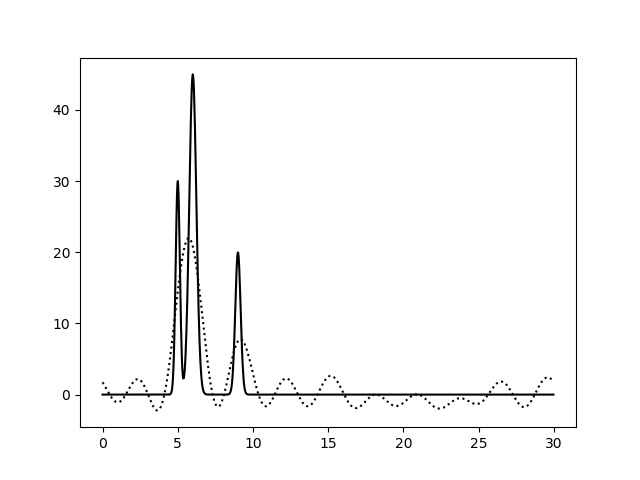 | 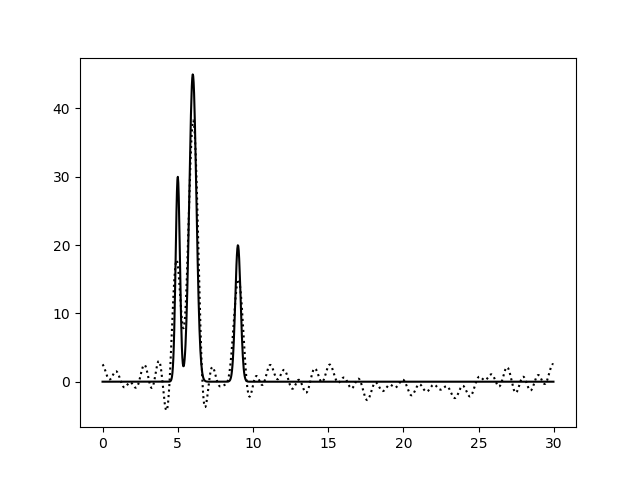 | 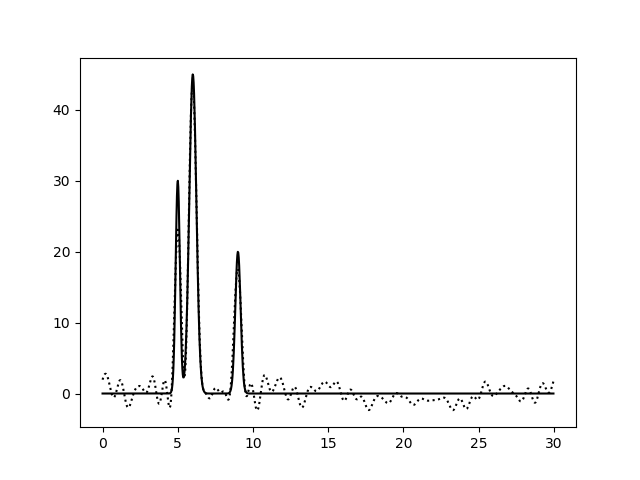 |
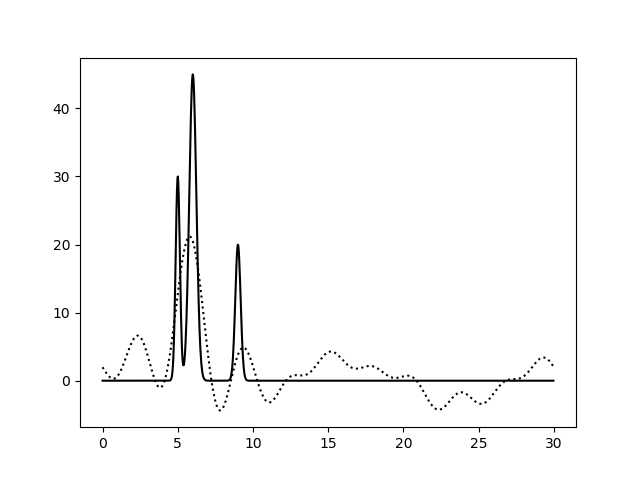
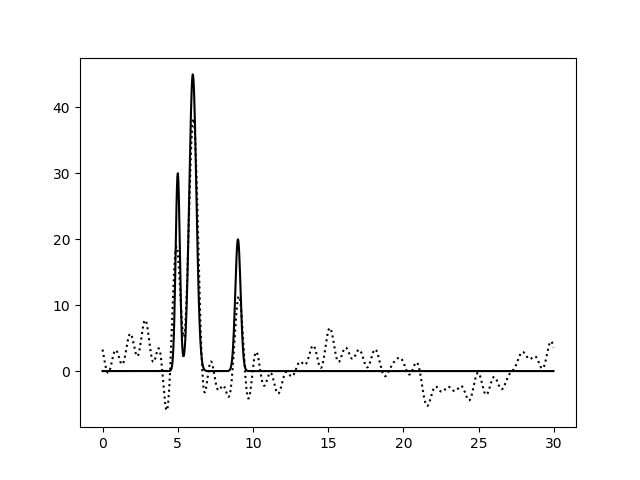
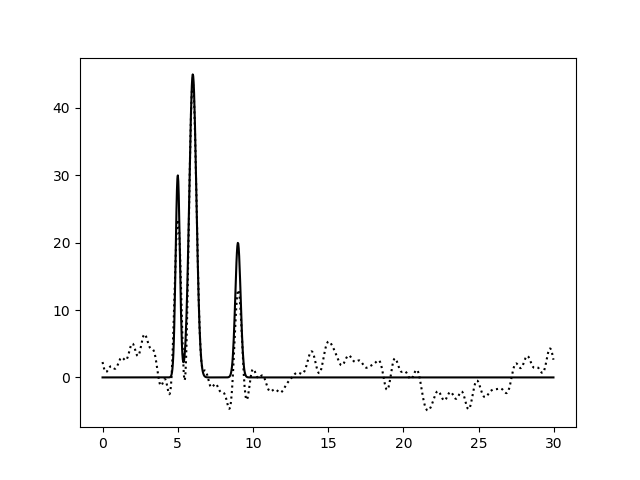
| Полный набор гармоник, с шумом (15% к амплитуде, 15% к фазе) |
| 0–10 | 0-30 | 0-40 |
 |  |  |
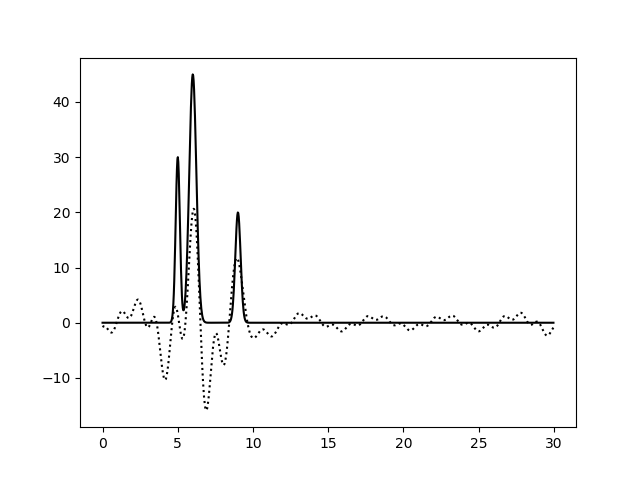
| Неполный набор гармоник, без шума |
| 7-46 | 7-26, 40-59 |
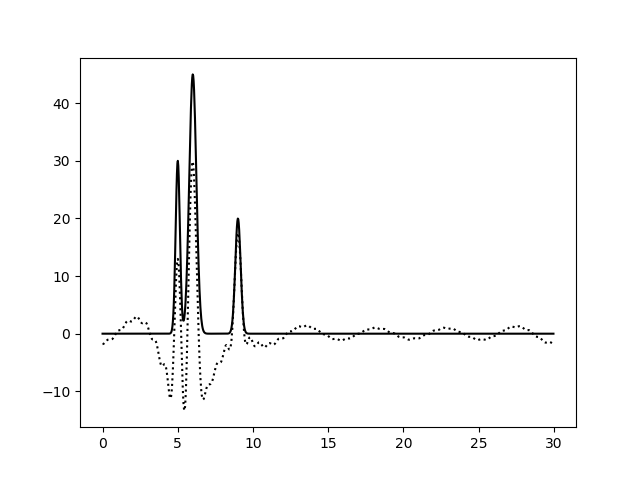 |  |
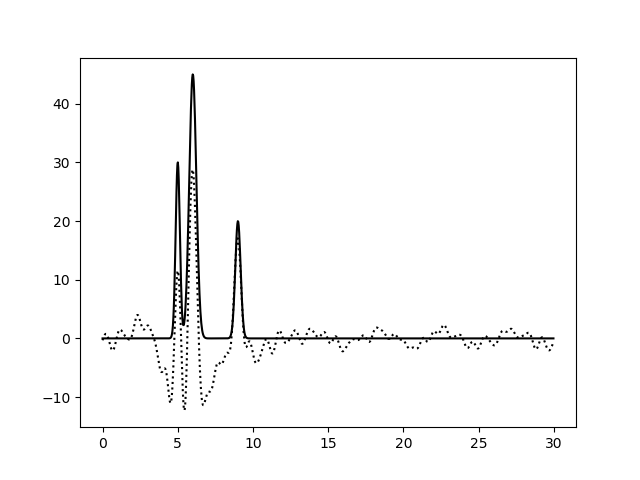
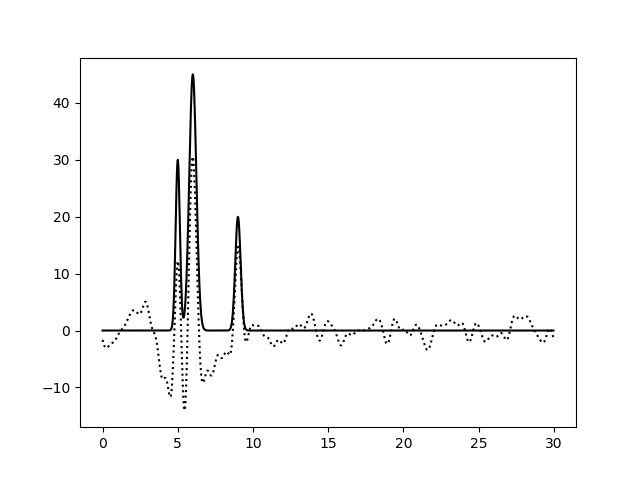
| Неполный набор гармоник, с шумом |
| 7-46, шум - 15% к амплитуде | 7-46, шум - 15% к амплитуде и фазам |
 |  |
4. Как сравнить восстановленную функцию с исходной
Для оценки отлично/хорошо/средне/плохо были использованы следующие критерии:
Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"
| Набор гармоник | Разрешение (A) | Полнота данных
(%) | Шум амплитуды (% от величины F) | Шум фазы
(% от величины phi) | Качество восстановления
(отличное, хорошее, среднее, плохое) |
| Полный набор гармоник |
| 0–10 | 3 | 100 | 0 | 0 | Плохое |
| 0–20 | 1,5 | 100 | 0 | 0 | Среднее |
| 0–30 | 1 | 100 | 0 | 0 | Хорошее |
| 0–40 | 0,8 | 100 | 0 | 0 | Отличное |
| 0–10 | 3 | 100 | 15 | 0 | Плохое |
| 0–30 | 1 | 100 | 15 | 0 | Хорошее |
| 0–40 | 0,8 | 100 | 15 | 0 | Отличное |
| 0–10 | 3 | 100 | 15 | 15 | Плохое |
| 0–30 | 1 | 100 | 15 | 15 | Хорошее |
| 0–40 | 0,8 | 100 | 15 | 15 | Отличное |
| Неполный набор гармоник |
| 7–46 | 0,5 | 68 | 0 | 0 | Хорошее |
| 7–26, 40–59 | 0,65 | 87 | 0 | 0 | Среднее |
| 7–46 | 0,5 | 68 | 15 | 0 | Хорошее |
| 7–46 | 0,5 | 68 | 15 | 15 | Хорошее |
Выводы: n0 (количество гармоник, при которых восстановение отличное) для модели без шума было равно ~40, для шума в амплитуде 15% тоже ~40, но заметно что оно всё-таки хуже, чем у модели без шума, для модели с шумом 15% и в амплитуде,
и в фазах при n=40 восстановление всего лишь хорошее. Можно также сравнивать соответственные восстановления этих трёх множеств на гармониках 0-10, 0-30, 0-40. Качество падает с увеличением шума. Вывод: шум ухудшает восстановление (логично).
При удалении первых гармоник восстановление сильно ухудшилось. На модели без шума 40 гармоник (n0 из 1 пункта) не с начала дают модель хорошего качества, а не отличного. При уменьшении полноты данных (опять 40 гармоник, но из набора 7–26, 40–59) качество среднее.
Вывод: чем выше полнота данных, тем лучше восстановление, первые гармоники вносят большой вклад в качество восстановления.
В шумных моделях и неполным набором гармоник снова видно, что шум ухудшает качество (сравнить картинки), в таблице всё обозначено как хорошее.
Источники
|








