Фурье
1. Задание функции
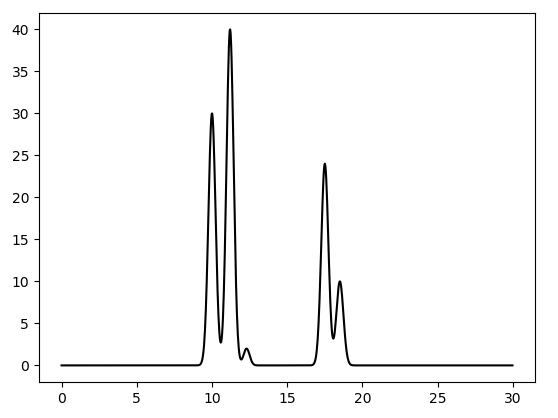
При помощи скрипта compile-func.py была смоделирована ЭП для системы в одномерной элементарной ячейке [0; 30Å]. Система состояла из двух молекул, находящихся на расстоянии ~3-4Å и содержащих 3 и 2 соединённых ковалентными связями атома соответственно. (Рис. 1)
Рис. 1. Сгенерированная ЭП
Генерация была проведена при помощи следующей команды:
python2 compile-func.py -g 30,3,10+40,3,11.2+2,3.5,12.3+24,3,17.5+10,3,18.5Параметр -g принимает на вход описание комбинации гауссиан. Каждая тройка соответсвует одной гауссиане, а именно трём параметрам, её задающим: α, β и γ.
Alpha и beta определяют форму, а gamma — положение пика.
2. Полные наборы гармоник
Разложение Фурье, т.е. расчет амплитуд и фаз сигналов, моделирующих ЭП, производился при помощи скрипта func2fourier.py Выдача скрипта содержала в себе параметры 500 гармоник (0-499). Для восстановления сигнала по коэффициентам использовался скрипт fourier2func.py.
Для определения минимально достаточного числа гармоник, в комбинации дающих отличное качество восстановления, были рассмотрены различные сабсеты 0-n, где n ≤ 60. Результаты этого эксперимента представлены на Рис. 2.
Рис. 2. Восстановление по наборам из первых n гармоник (n ≤ 60)
Каждый из приведенных ниже примеров проиллюстрирован отдельно на Рис. 3.
При n=5 наблюдается восстановление плохого качества: удается примерно определить положения молекул и их размеры, но отдельные атомы в их составе на данном этапе неразличимы.
При n=20 становится возможным определить с некоторой точностью положения четырёх из пяти атомов. Это пример восстановления со средним качеством.
По мере дальнейшего увеличения числа гармоник (n=30) амплитуды мощных сигналов приближаются к реальным и, зная число атомов, можно определить положения всех максимумов (хорошее качество). Однако, в силу наличия низкого пика #3 (атома с небольшим числом электронов), на данном этапе очень сложно разделить настоящий сигнал и фоновый шум, особенно интенсивный на участке между молекулами.
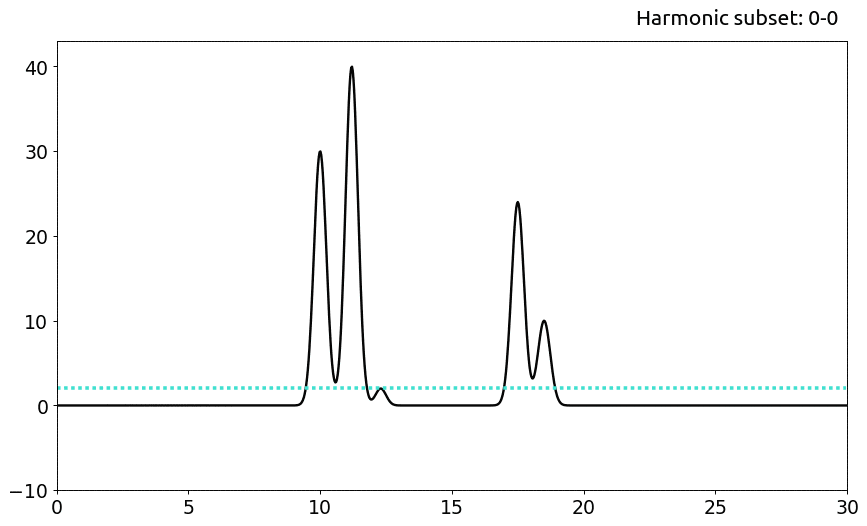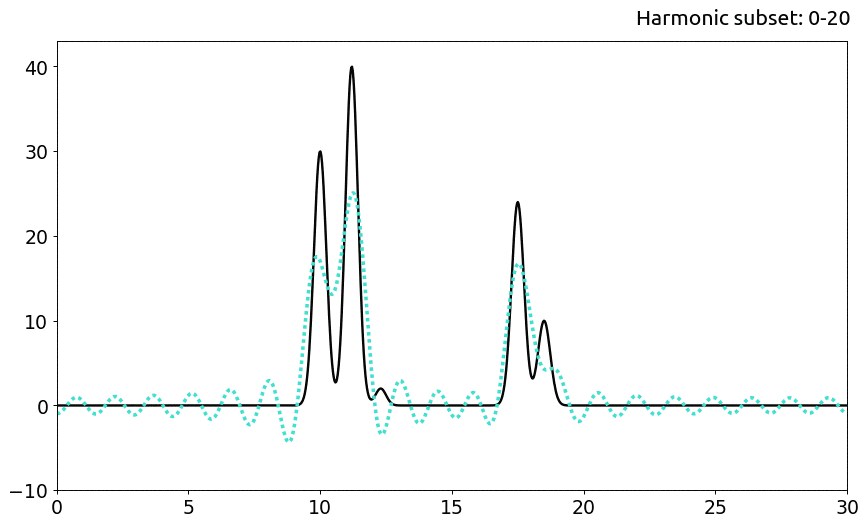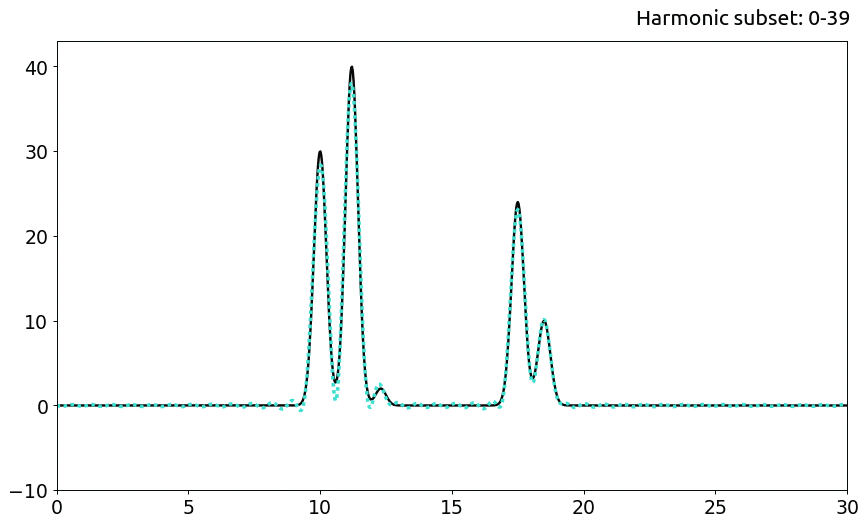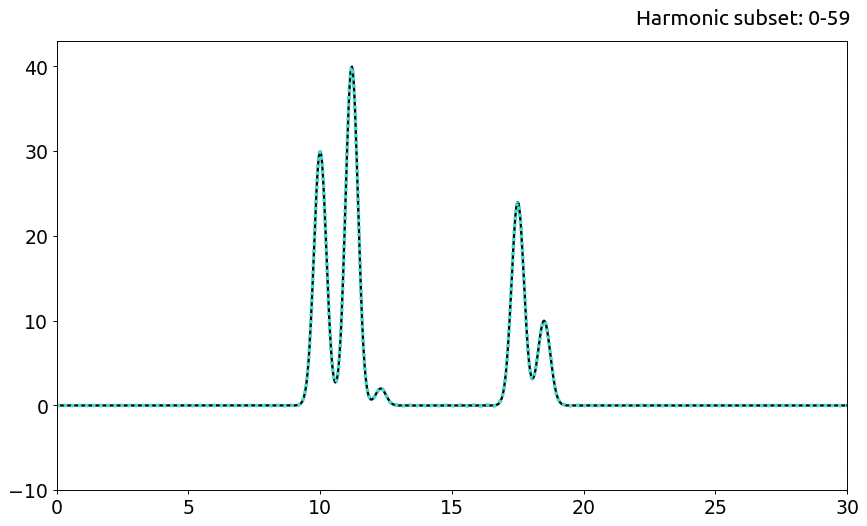
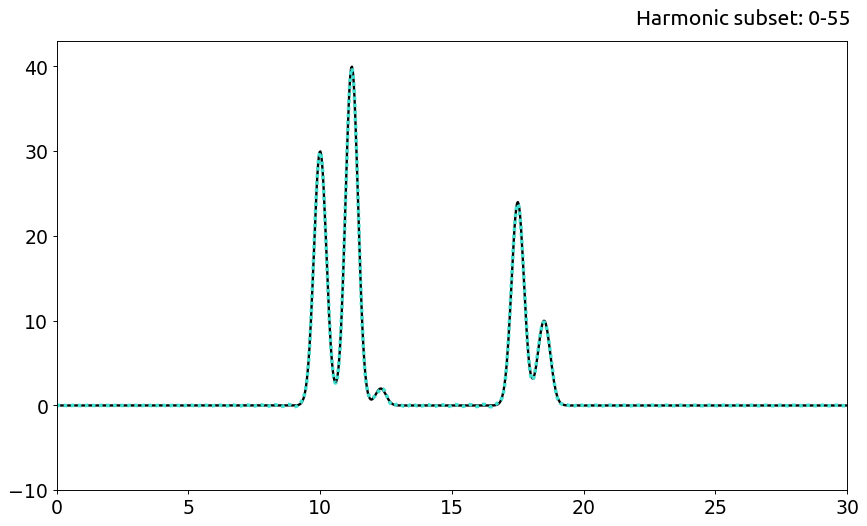
Что вполне ожидаемо, с повышением числа гармоник шум становится практически равным нулю, а амплитуды восстановленного сигнала приближаются к настоящим. Отличное качество начинается с n=55.
Далее под минимальным набором гармоник будет подразумеваться сабсет 0-55.
Рис. 3. Различное качество восстановления сигнала
а. Плохое качество
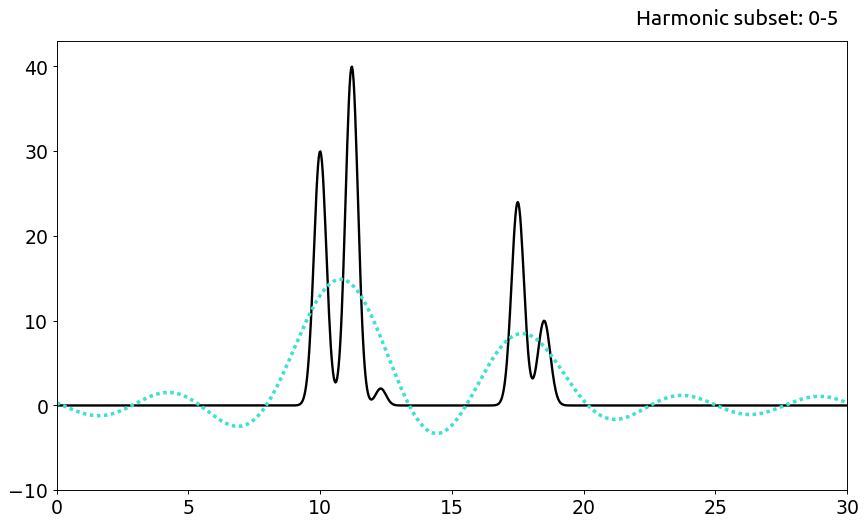
b. Среднее качество
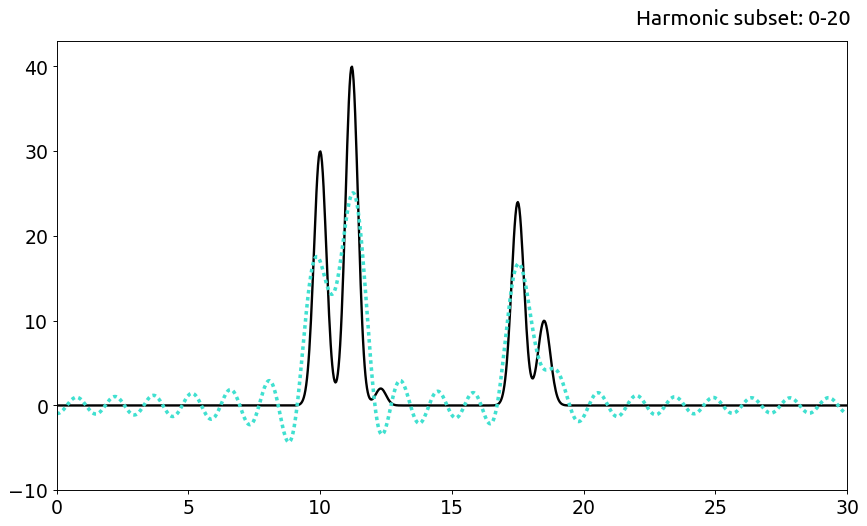
c. Хорошее качество
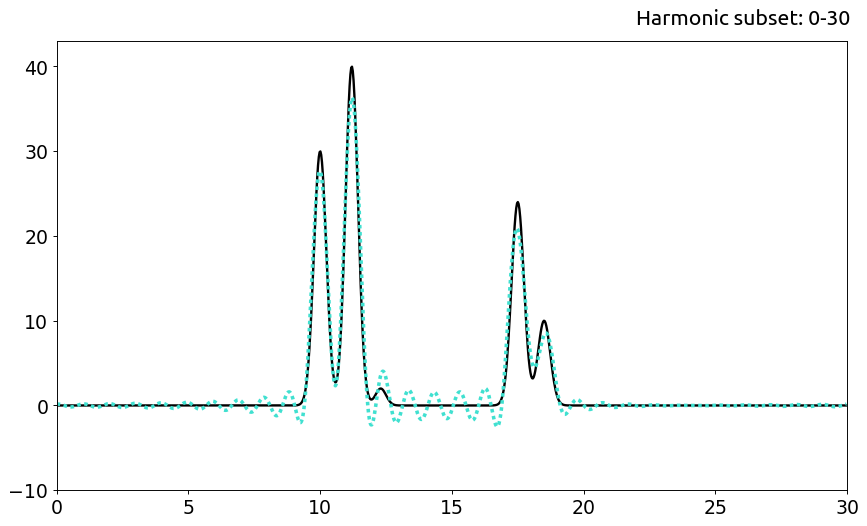
d. Отличное качество
Скрипт func2fourier.py также позволяет задать опции -F и -P,
которые определяют уровни гауссова шума, добавляемого к амплитудам и фазам соответственно. Именно эти параметры и использовались для генерации нескольких разложений Фурье различной зашумленности. На Рис. 4 приведены результаты восстановления функции по сабсету гармоник 0-55 при разных значениях шума: 0%, 10% и 20%.
Рис. 4. Восстановление сигнала по зашумленным данным
Cкролл вниз соответствует увеличению шума амплитуд, скролл вправо — увеличению шума фаз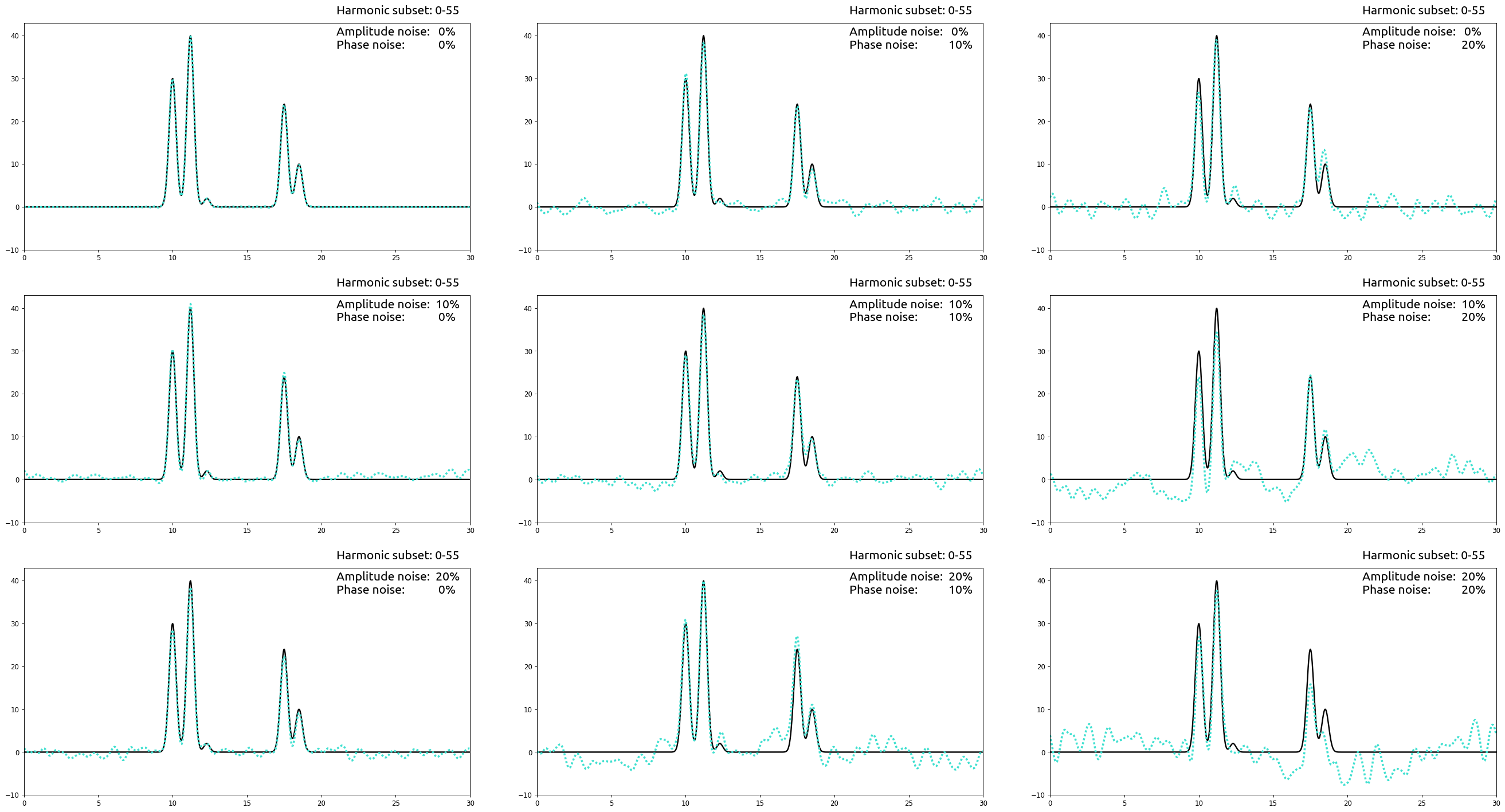
При повышении уровней шума ожидаемо падает качество восстановления. Из приведенных экспериментов можно сделать вывод о том, что шум по фазе сильнее ухудшает результат, нежели шум по амплитудам.
3. Неполные наборы гармоник
В этой части работы проводилось исследование качества восстановления при использовании неполных наборов гармоник.
Удаление первых k гармоник. Проводилось для значений k=[1, 2, 7]. Результаты восстановления приведены на Рис. 5.
Рис. 5. Удаление первых k гармоник
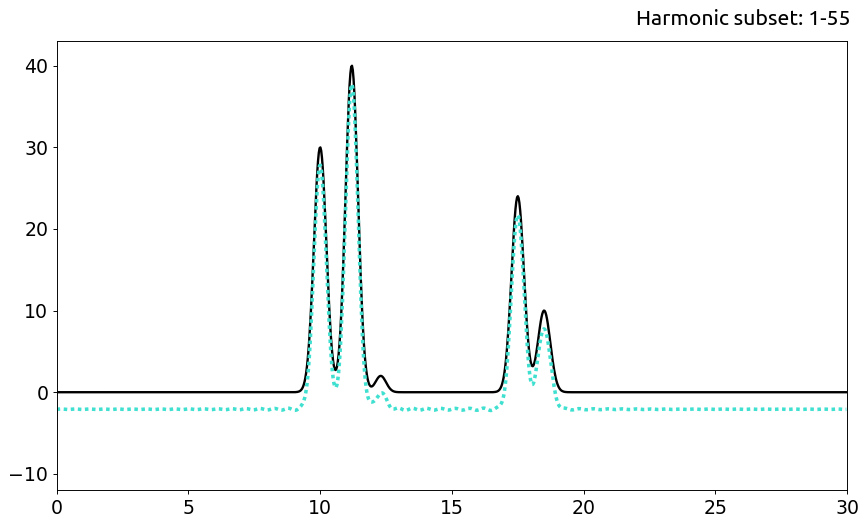
а. Сабсет гармоник 1-55
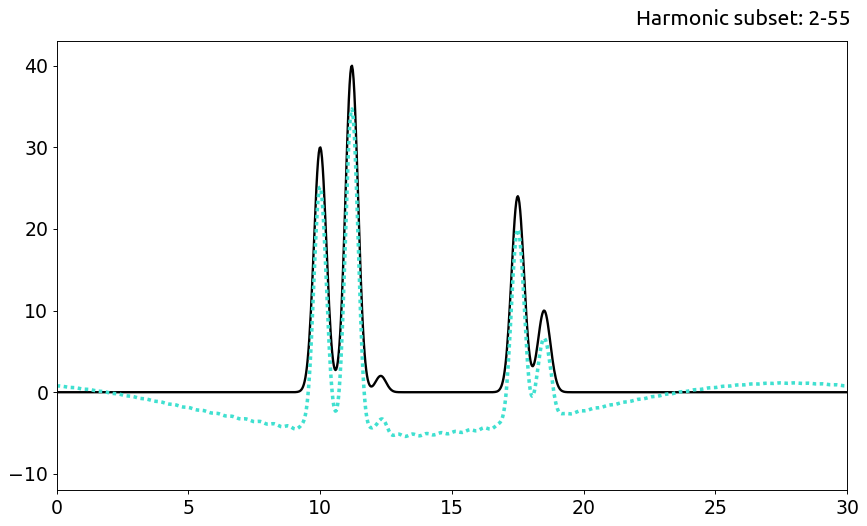
b. Сабсет гармоник 2-55
c. Сасбсет гармоник 7-55
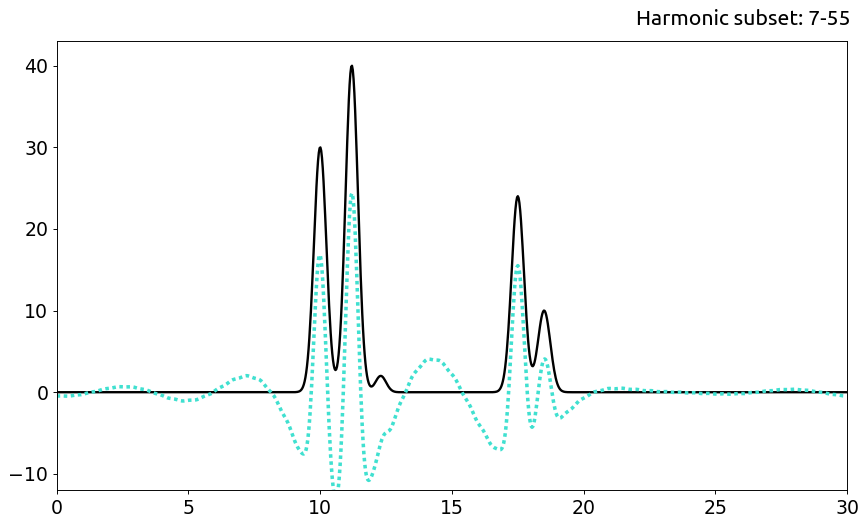
При исключении гармоники #0 происходит только сдвиг по оси Оу на некую константу, поскольку эта гармоника представляет собой свободный член ряда Фурье. При удалении первых двух гармоник все так же можно распознать положения всех атомов. В случае же отбрасывания первых семи гармоник качество воссстановления ухудшается гораздо сильнее: позиции мощных пиков изначальной функции все еще можно найти, но более низкие пики имеют интенсивность, сравнимую с уровнем шума.
Удаление последовательных гармоник из разных частей ряа. Были опробованы варианты с отбрасыванием трех гармоник из областей, близких к а. началу, б. середине, в. концу ряда. Соответствующие графики, иллюстрирующие восстановление, приведены на Рис. 6.
Рис. 6. Удаление трёх гармоник из разных частей ряда
а. Сабсет гармоник 0-4,8-55
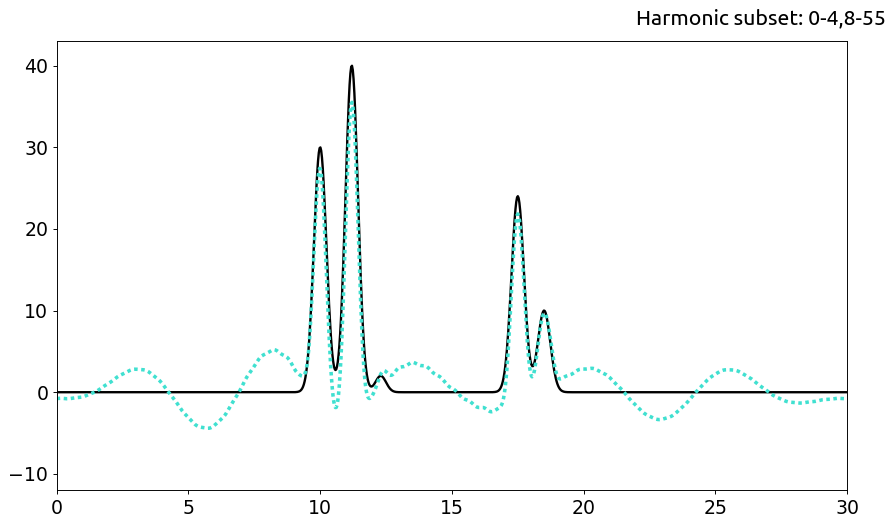
b. Сабсет гармоник 0-24,28-55
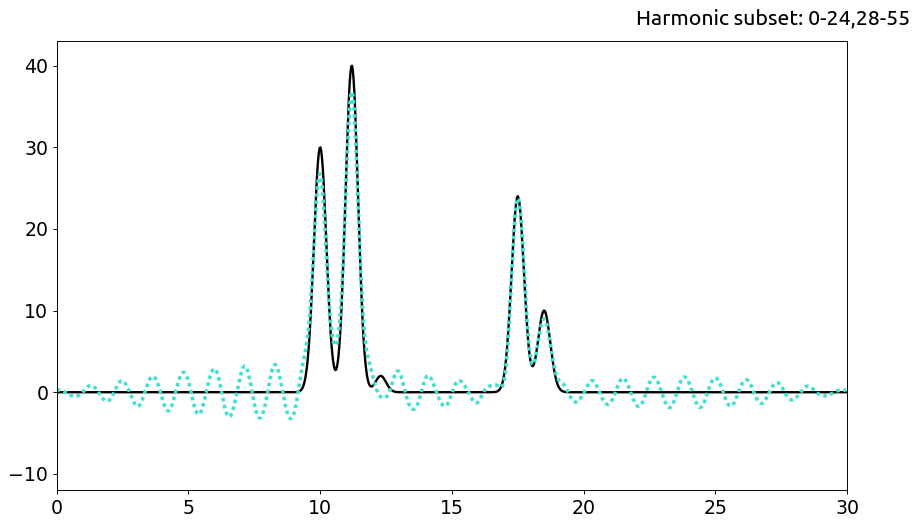
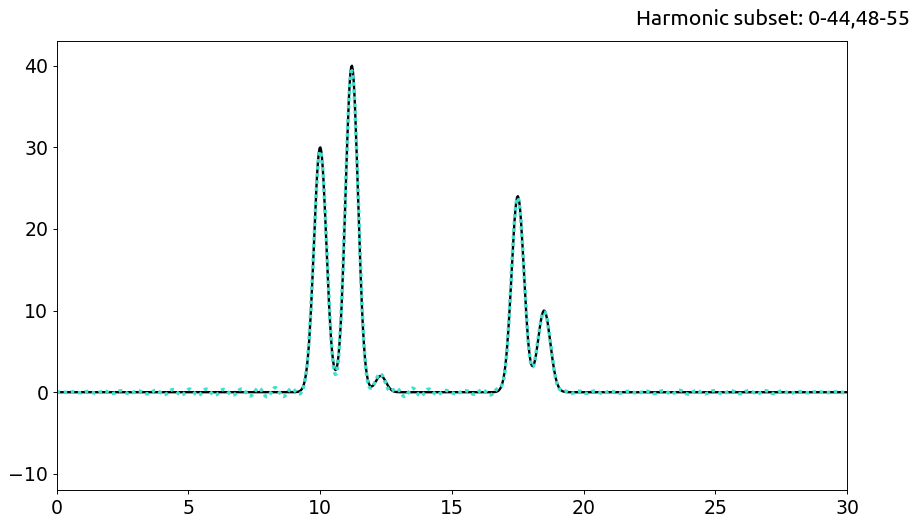
c. Сасбсет гармоник 0-44,48-55
Данный эксперимент наглядно показывает, что гармоники, близкие к началу ряда имеют большее влияние на качество восстановления функции, поскольку при их отбрасывании качество падает сильнее. Так, исключив три близкие к началу гармоники (#5-7), мы уже не можем назвать качество восстановления отличным: положения атомов с высокими пиками определяется достаточно точно, но для атома #3 с низкой амплитудой пика это не так — его невозможно вычленить из-за значительного уровня шума.
Подобная проблема наблюдается и при удалении гармоник #25-27 из середины. Но стоит отметить, что это так в силу действительно небольшой настоящей амплитуды атома #3. Если бы рассматривалась система без него, уровень шума вполне можно было бы считать некритичным.
В свою очередь, гармоники 45-47, исключенные из конца ряда, практически не повлияли на качество восстановления: его все так же можно считать отличным, и уровнем шума можно спокойно пренебречь.
Добавление гармоники за пределами сабсета 0-55. В данном случае к сабсету 0-55, минимально достаточному для достижения отличного качества восстановления, была добавлена гармоника 65. Результат восстановления функции ЭП по этому множеству гармоник представлен на Рис. 7.
Рис. 7. Добавление гармоники в конец: 0-55,65
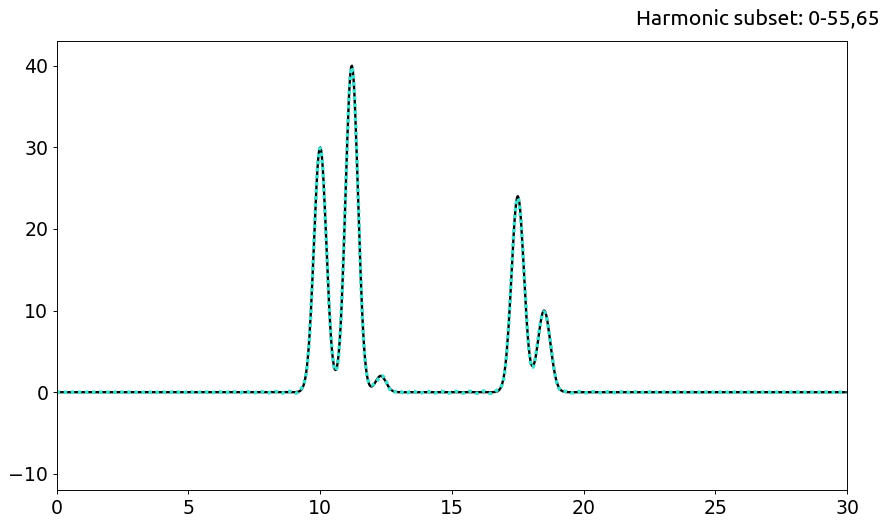
Добавление гармоники 65 не оказало никакого существенного влияния на качество восстановления по сравнению с сабсетом 0-55.
4. Подведение итогов
В данном разделе проведено суммирование всех поставленных экспериментов по влиянию набора гармоник на качество восстановления функции ЭП в одномерной элементарной ячейке. Результаты представлены в Таблице 1.
Таблица 1. Восстановление функции по коэффициентам ряда Фурье
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум аплитуды (% от величины F) |
Шум фазы (% от величины φ) |
Качество восстановления |
| Полные наборы гармоник без зашумления | |||||
| 0-5 | 6.000 | 100% | 0 | 0 | плохое |
| 0-20 | 1.50 | 100% | 0 | 0 | среднее |
| 0-30 | 1.000 | 100% | 0 | 0 | хорошее |
| 0-55 | 0.545 | 100% | 0 | 0 | отличное |
| Полные наборы гармоник с внесением шума | |||||
| 0-55 | 0.545 | 100% | 10 | 0 | хорошее |
| 0-55 | 0.545 | 100% | 20 | 0 | хорошее |
| 0-55 | 0.545 | 100% | 0 | 10 | среднее |
| 0-55 | 0.545 | 100% | 10 | 10 | среднее |
| 0-55 | 0.545 | 100% | 20 | 10 | плохое |
| 0-55 | 0.545 | 100% | 0 | 20 | среднее |
| 0-55 | 0.545 | 100% | 10 | 20 | плохое |
| 0-55 | 0.545 | 100% | 20 | 20 | плохое |
| Неполные наборы гармоник | |||||
| 1-55 | − | 98% | 0 | 0 | отличное |
| 2-55 | − | 96% | 0 | 0 | отличное |
| 7-55 | − | 87.5% | 0 | 0 | среднее |
| 0-4,8-55 | − | 95% | 0 | 0 | отличное |
| 0-24,28-55 | − | 95% | 0 | 0 | среднее |
| 0-44,48-55 | − | 95% | 0 | 0 | хорошее |
| 0-55,65 | − | 84% | 0 | 0 | отличное |