Описание сигнала, закодированного в геноме
Аденоассоциированный вирус (AAV) является интересным кандидатом на вирусный вектор для генной терапии. Его дикие разновидности инфицируют клетки человека и некоторых других приматов, встраиваясь в участок 19 хромосомы (19q13.2-13.4qtr у человека), называемый AAVS1. Данный сигнал представляет из себя обширный участок размером около 4800 bp, на концах которого расположены инвертированные повторы (ITR). Они необходимы для интеграции вируса в сайт AAVS1 [1] (по сути, вирус является адресатом). Эффективность интеграции вируса в геном человека разнится от исследования к исследованию. Здесь [2], например, авторы дают оценку в 68%, а в данной работе [3] максимальная эффективность интеграции составила около 40%.
Источники:
- https://en.wikipedia.org/wiki/Adeno-associated_virus
- Kotin RM, Siniscalco M, Samulski RJ, Zhu XD, Hunter L, Laughlin CA, McLaughlin S, Muzyczka N, Rocchi M, Berns KI. Site-specific integration by adeno-associated virus. Proc Natl Acad Sci U S A. 1990 Mar;87(6):2211-5. doi: 10.1073/pnas.87.6.2211. PMID: 2156265; PMCID: PMC53656.
- Hamilton H, Gomos J, Berns KI, Falck-Pedersen E. Adeno-associated virus site-specific integration and AAVS1 disruption. J Virol. 2004 Aug;78(15):7874-82. doi: 10.1128/JVI.78.15.7874-7882.2004. PMID: 15254160; PMCID: PMC446113.
P.S. Интересно поразмышлять о том, является ли описанное явление сигналом в принципе: у него есть получатель, и узнается вирусом он с неплохой эффективностью, однако адресанта у него нет (клетке не требуется интеграция вируса в свою ДНК, в отличие от, например, трансляции).
PWM для нуклеотидного сигнала
В данном задании требуется построить позиционно-весовую матрицу (PWM) для сигналов, заданных выравниванием нуклеотидных последовательностей, и оценить сделанные по ней предсказания новых сигналов. В качестве такого сигнала я выбрала регуляторный элемент PyrR, связывание регуляторных факторов с которым контролирует биосинтез пиримидинов (формируется шпилька в downstream-регионе, подавляя экспрессию соответствующих генов). Таким образом, этот бактериальный регуляторный элемент участвует в аттенюации.
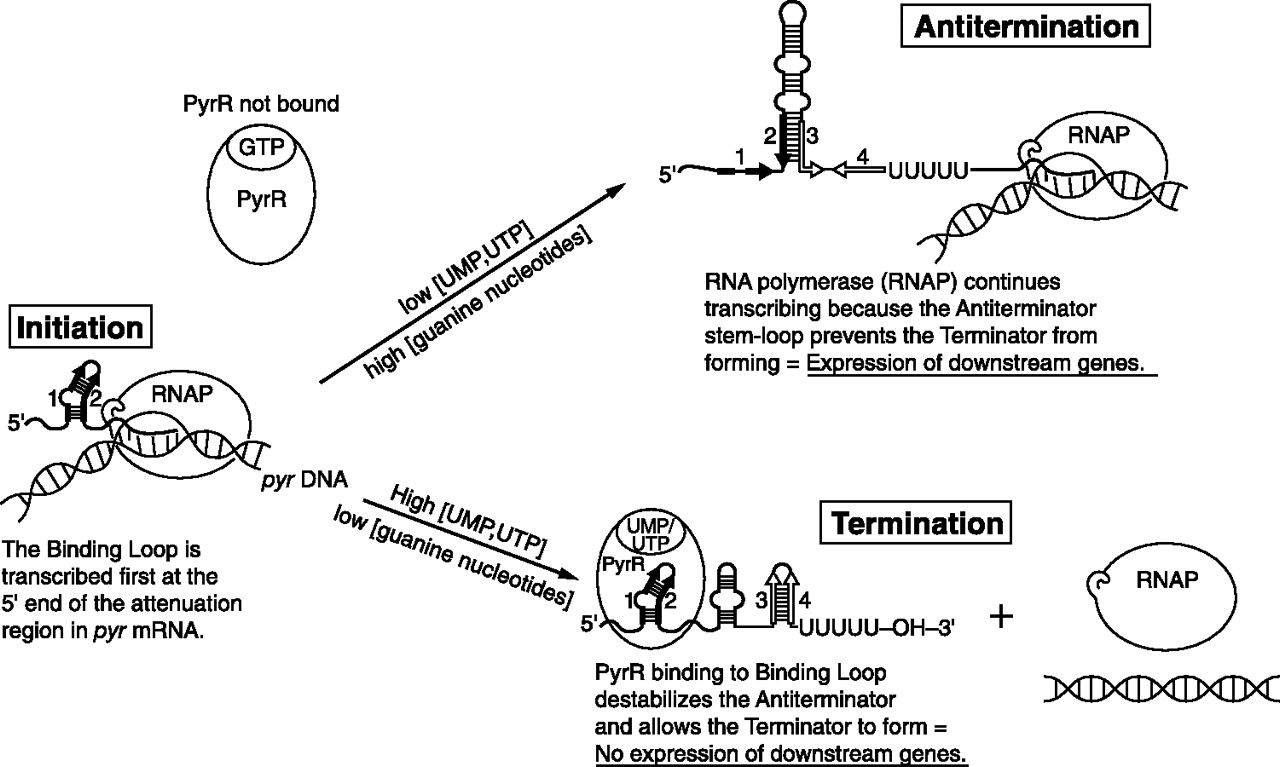
Последовательности были взяты из базы данных RFAM. Для тренировочной выборки, по которой строится PWM, я взяла последовательности, помеченные как seed, всего их 41, в тестововую выборку было взято 82. В RFAM хранятся последовательности, содержащие только интересующий участок и его окрестности. Для получения выравнивания тренировочных последовательностей без гэпов я взяла небольшой участок, выделенный цветом -- по литературным данным он может играть важную роль в данном процессе, к тому же, в нем присутствует большое число высококонсервативных позиций (что в некодирующих регионах редко встречается просто так). Файл с этими последовательностями можно найти здесь, тут - тестовые.

В качестве негативного контроля выступили другие фрагменты этих же последовательностей аналогичной длины. Вся обработка проводилась в Python с использованием пакета BioPython (скрипт). Поскольку последовательности рассматриваемого сайта взяты из различных бактерий, значения псевдоотсчетов определены как 0.5.
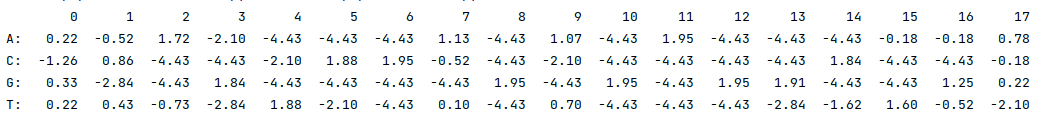
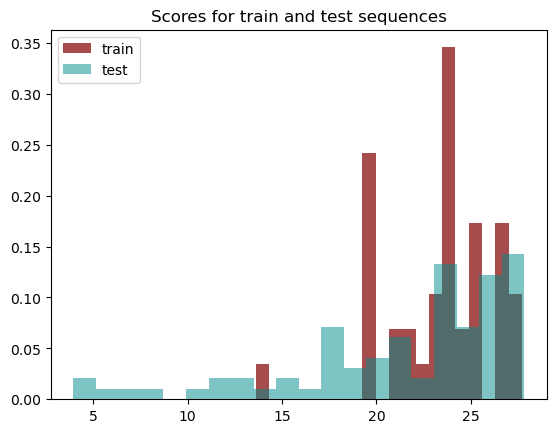
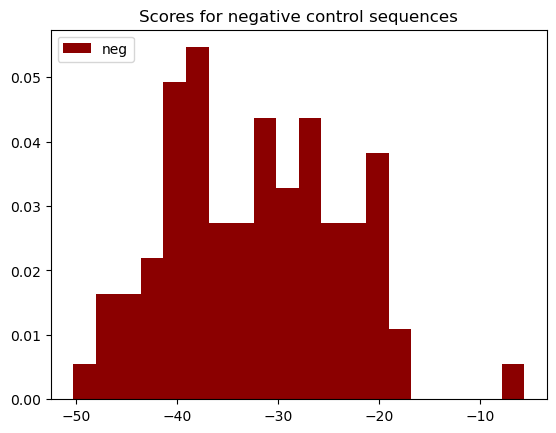
Были построены диаграммы счетов для трех выборок. Значения отрицательного контроля вынесены на отдельную гистограмму, т.к. счета для таких последовательностей очень маленькие.
Порог счета для нахождения мотива был подсчитан с помощью пакета BioPython и равен 9.58 (отношение между вероятностью ошибок первого и второго рода равно 1000). Это значение соотносится с распределениями на гистограмме. Возможно, отрицательные значения счетов контрольной выборки получились из-за большого размера мотива. Гипотетически, было бы лучше взять последовательности, связывающие сходные белки, а не просто случайно выбранные + увеличить размер выборки. В целом, наблюдаемые результаты были ожидаемы :)
Частоты и количества результатов поиска мотивов в тренировочной, тестовой и случайной выборках
| Тренировочная | Тестовая | Отрицательный контроль | |
| "+"-сигнал | 41/41 (100%) | 77/82 (93%) | 0/82 (0%) |
| "-"-сигнал | 0/41 (0%) | 5/82 (6%) | 82/82 (100%) |
Информационное содержание
С помощью все того же пакета BioPython, а также библиотеки Pandas, была построена матрица информационного содержания (в скрипте генерируется как вторая матрица)

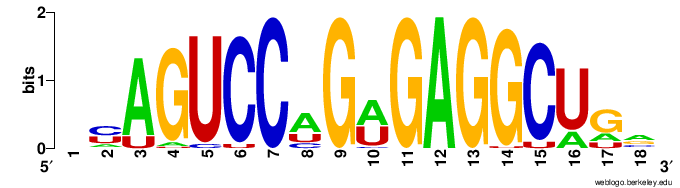
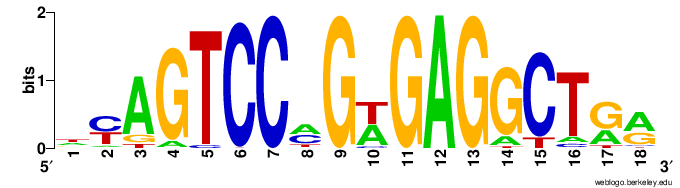
По последовательностям тренировочной выборки (слева) были построены LOGO. Дополнительно прилагаю аналогичное изображение для тестовой выборки (справа), для сравнения.
Оценка количества участков GAATTC в геноме E.Coli
Для работы был выбран E.Coli O157:H7 str. Sakai (референсный геном). У нее есть плазмиды, но мы будем рассматривать только саму хромосому. Теоретическое значение можем посчитать, перемножив частоты соответствующих нуклеотидов (GC-content=50.5%) на размер генома (5 498 578 bp), для данного штамма это около 1315. Реальное значение сильно отличается - найден 721 такой участок. p-value для таких значений, посчитанное с помощью Z-теста (Z=1295.1), слишком маленькое, чтобы отображаться в онлайн-калькуляторе. Таким образом, различия данных значений достоверны.
I don't know how to make footer properly. You may as well pretend you haven't seen this phrase!