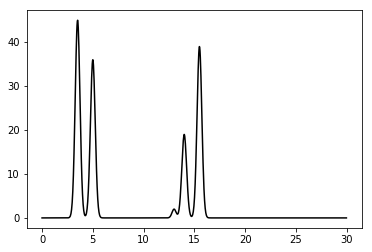
Модельная функция ЭП в одномерной элементарной ячейке была задана как сумма пяти гауссовых функций:
gauss = 45e-32(x-3.5)2 +
36e-32(x-5)2 +
2e-3.52(x-13)2 +
19e-32(x-14)2 +
39e-32(x-15.5)2
Команда для задания функции:
run 'compile-func.py' -g 45,3,3.5+36,3,5+2,3.5,13+19,3,14+39,3,15.5

Рисунок 1. Модельная функция электронной плотности
Далее были рассчитаны параметры сигнала, моделирующие экспериментальные данные: амплитуды и фазы.
run 'func2fourier.py' func.txt
Отбор гармоник производился с помощью запуска с различными параметрами функции:
run 'fourier-filter.py' -r 0-42
Восстановление функции ЭП по модельным ("экспериментальным") данным
run 'fourier2func.py' -f func.txt -i func_ft_filtered.txt -o two_func.txt
Оценка качества восстановления функции ЭП
Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы атомов не отличимы от шума
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"
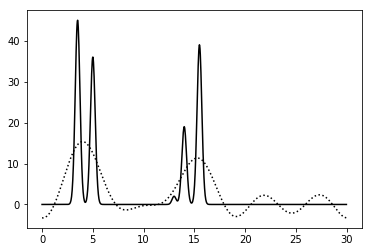
Рисунок 2. График функции, восстановленной по гармоникам с 1 по 5. |
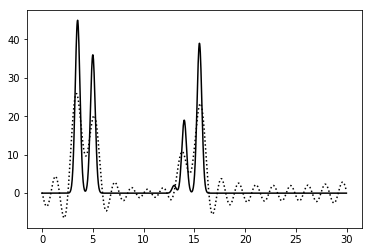
Рисунок 3. График функции, восстановленной по гармоникам с 1 по 17. |
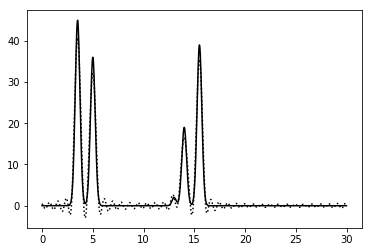
Рисунок 4. График функции, восстановленной по гармоникам с 1 по 36. |
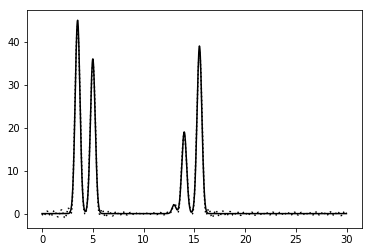
Рисунок 5. График функции, восстановленной по гармоникам с 1 по 42. |
Отличное восстановление было получено при использовании полного набора гармоник от 0 до 42.
Для зашумления исходной функции амплитуда и фаза рассчитывались с использованием дополнительных параметров, задающих добавление гауссового шума к амплитудам (параметр -F <число>) и фазам (-P <число>):
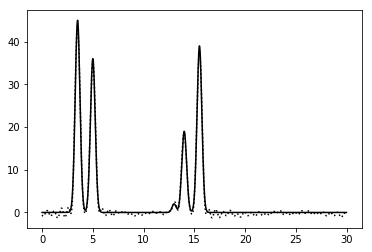
Рисунок 6. График функции, восстановленной по гармоникам с 0 по 42 при добавлении к амплитудам шума на уровне 5%. |
|
|
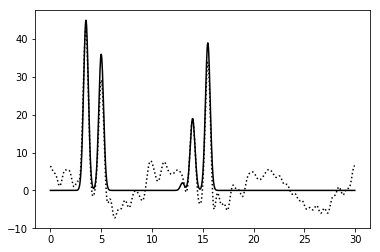
Рисунок 7. График функции, восстановленной по гармоникам с 0 по 42 при добавлении к фазам шума на уровне 10%. |
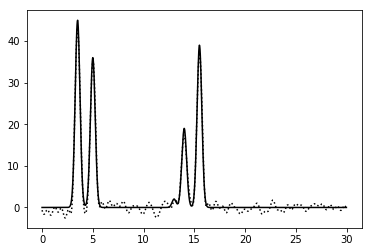 Рисунок 8. График функции, восстановленной по гармоникам с 0 по 42 при добавлении к амплитудам шума на уровне 5% и к фазам шума на уровне 5%. |
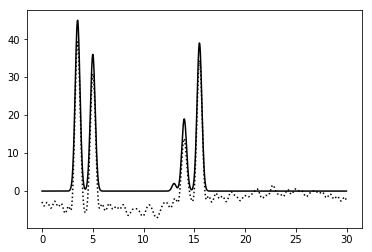
Рисунок 9. График функции, восстановленной по гармоникам со 2 по 42. |
|
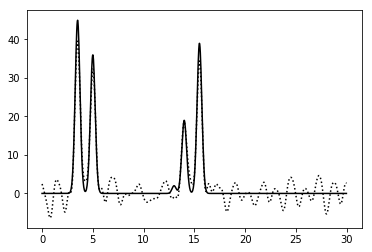
Рисунок 10. График функции, восстановленной по гармоникам 0-10, 13-20, 23-42. |
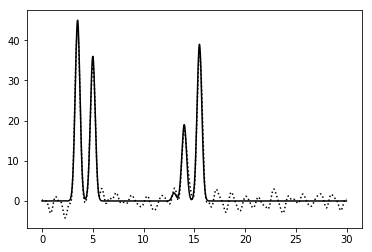
Рисунок 11. График функции, восстановленной по гармоникам 0-10, 12-20, 22-32, 34-42. |
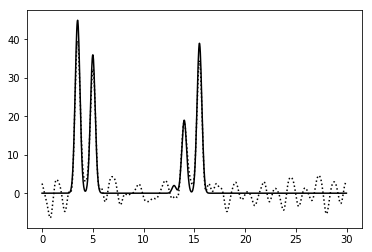
Рисунок 12. График функции, восстановленной по гармоникам 0-10, 13-20, 23-42, 52. |
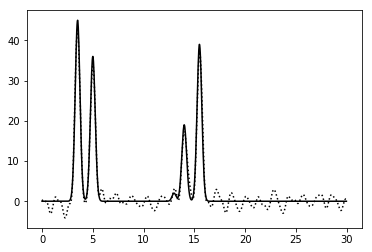
Рисунок 13. График функции, восстановленной по гармоникам 0-10, 12-20, 22-32, 34-42, 52. |
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум амплитуды (% от величины F) |
Шум фазы (% от величины phi) |
Качество восстановления (отличное, хорошее, среднее, плохое) |
Комментарии |
Полный набор гармоник |
||||||
| 0-5 | 6 | 100 | 0 | 0 | Плохое | |
| 0-17 | 1.8 | 100 | 0 | 0 | Среднее | |
| 0-36 | 0.8 | 100 | 0 | 0 | Хорошее | |
| 0-42 | 0.7 | 100 | 0 | 0 | Отличное | |
| 0-42 | 0.7 | 100 | 5 | 0 | Хорошее | |
| 0-42 | 0.7 | 100 | 0 | 10 | Среднее | |
| 0-42 | 0.7 | 100 | 5 | 5 | Среднее | |
Неполный набор гармоник |
||||||
| 2-42 | 0.7 | 95 | 0 | 0 | Хорошее | |
| 0-10,13-20,23-42 | 1 | 86 | 0 | 0 | Среднее | |
| 0-10,12-20,22-32,34-42 | 0.7 | 93 | 0 | 0 | Хорошее | |
| 0-10,13-20,23-42,52 | 1 | 86 | 0 | 0 | Среднее | |
| 0-10,12-20,22-32,34-42,52 | 0.7 | 93 | 0 | 0 | Хорошее | |