Качество восстановления ЭП

Качество восстановления функции ЭП по гармоникам Фурье

Создание функции ЭП

Модель для компьютерного эксперимента: на отрезке [0,30] (ангстремы) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 ангстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Всего 5-7 атомов (2+3 или 2+3+2; возможны другие варианты). Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.
Функция задается на интервале [0,30]. Моделируется в 1D график электронной плотности молекулы. Функция имеет вид нескольких гауссовых кривых с центром в разных точках. Иногда - на расстоянии 1-1.5 ангстрем - модель ковалентно связанных атомов; иногда 3-5 ангстрем.
Функция создаётся скриптом compile-func.py. Гауссова функция определяется числами λ, β, γ по формуле: gauss = λ*exp(-(β^2)*(X-γ)^2).

Был выбран вариант 7, где заданы высоты, широты и координаты максимума пика соответственно. Эти данные были даны на вход скрипту, создающему функцию ЭП командой:

python compile-func.py -g 10,2,5+10,2,7+30.0,2,12+30.0,2,16+30.0,2,22+30,2,24

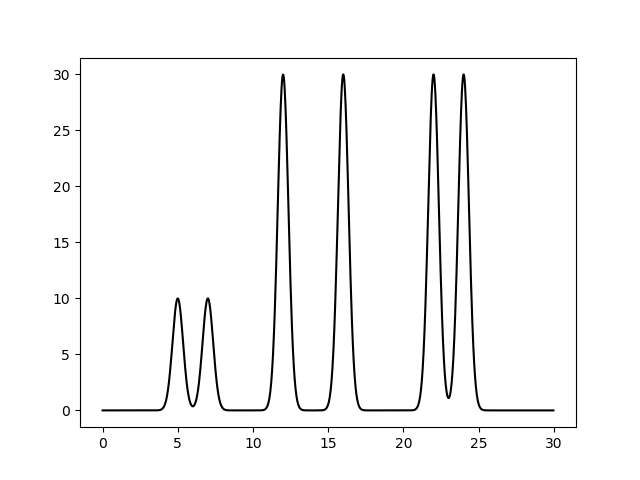
Указанный скрипт выдал текстовый файл func.txt и изображение функции электронной плотности (см рис 1). В данном случае система состоит из 6 атомов.

Рисунок 1. Изображение функции электронной плотности, полученное в результате компьютерного эксперимента.

Расчет коэффициентов Фурье

Для функции ЭП, полученной на предыдущем этапе, были рассчитаны амплитуды и фазы сигналов с помощью скрипта func2fourier.py командой:

python func2fourier.py -i func.txt

func_ft.txt

Отбор необходимого числа гармоник и восстановление исходной функции ЭП по полному набору гармоник

Из полученных 499 гармоник было отобрано необходимое для восстановления функции количество гармоник. Скрипт, фильтрующий гармоники, - fourier-filter.py. Параметр -r позволяет отфильтровать гармоники с указанными номерами.

python fourier-filter.py func_ft.txt -r 0-5

Для визуализации результата фильтрации был использован скрипт fourier2func.py, входным файлом для которого служил выходной файл фильтрующего скрипта. Команда ниже:

python fourier2func.py func_ft_filtered.txt

Так как нам известно разрешение всех гармоник в наборе, этот набор гармоник полный. В зависимости от того, сколько гармоник будут выбраны для восстановления ЭП, качество реконструкции будет разным. Качество восстановления характеризуется так:

Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов").
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума.
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно.
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".

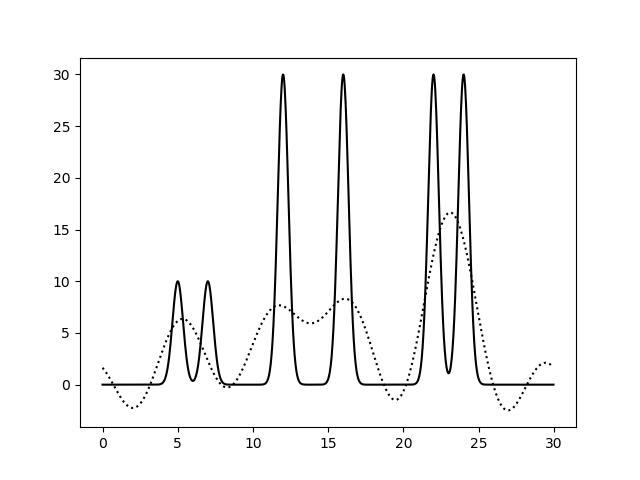
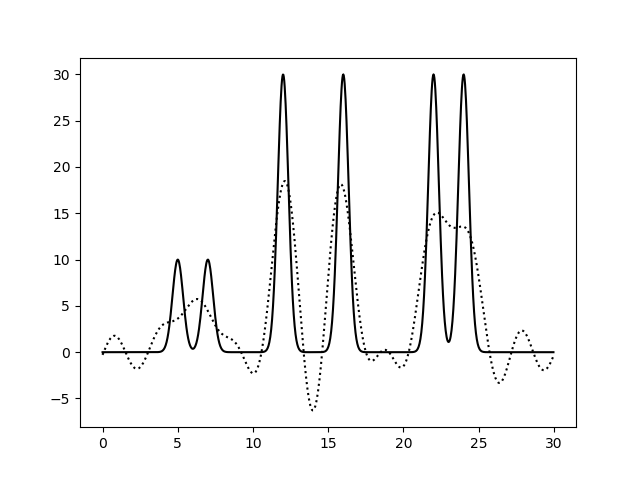
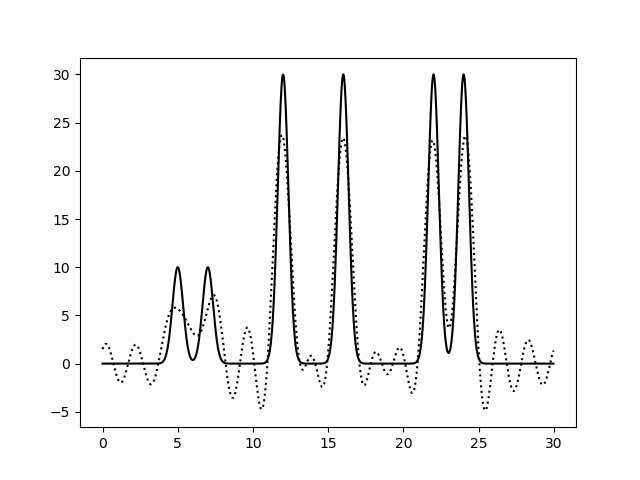
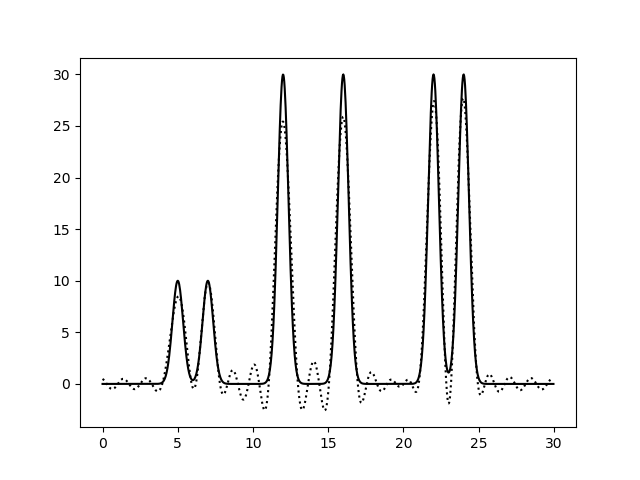
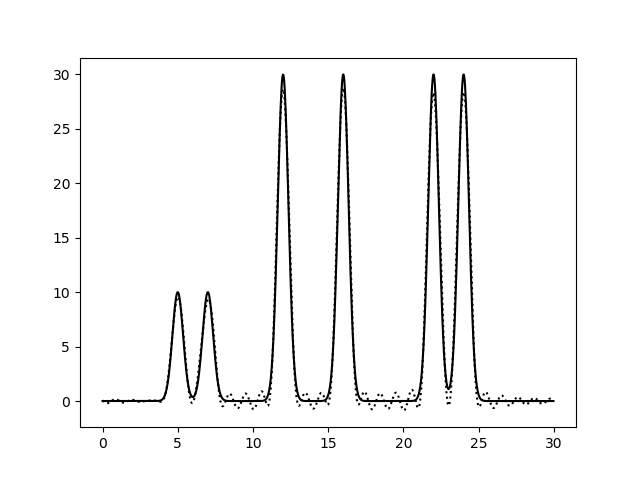
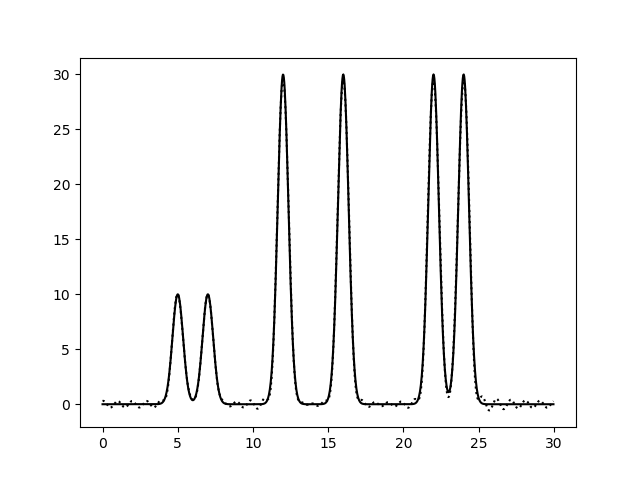
На рисунках 2-10 представлены графики функций ЭП, восстановленные по полным наборам гармоник разных размеров. Сплошной линией обозначен график исходной функции ЭП, пунктирной линией - восстановленной.

Судя по этим графикам, для отличного восстановления функции ЭП хватает полного набора гармоник от 0-й до 20-й. Набор из гармоник от 0-й до 30-й полностью повторяет функцию ЭП, в том числе точную высоту пиков. Дальнейшее увеличение количества гармоник в наборе уже не улучшает качества.

Рисунок 2. Гармоники от 0-й до 5-й. Рисунок 3. Гармоники от 0-й до 10-й. Рисунок 4. Гармоники от 0-й до 15-й.

Рисунок 5. Гармоники от 0-й до 20-й. Рисунок 6. Гармоники от 0-й до 27-й. Рисунок 7. Гармоники от 0-й до 30-й.

Восстановление исходной функции ЭП при добавлении гауссового шума к амплитудам и фазам

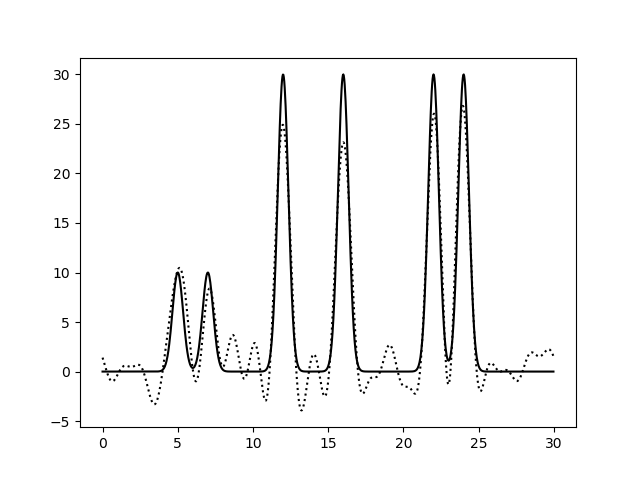
Чтобы сделать модель более приближенной к реальности, к амплитудам и фазам на стадии определения набора гармоник был добавлен гауссовский шум. Делается это с помощью параметров -F для амплитуд и -P для фаз. Для восстановления исходной функции использовался полный набор гармоник от 0-й до 20-й (как показано на предыдущем шаге, этого должно быть достаточно для отличного восстановления).

python func2fourier.py func.txt -F 20 -P 20
python fourier-filter.py func_ft.txt -r 0-20
python fourier2func.py func_ft_filtered.txt

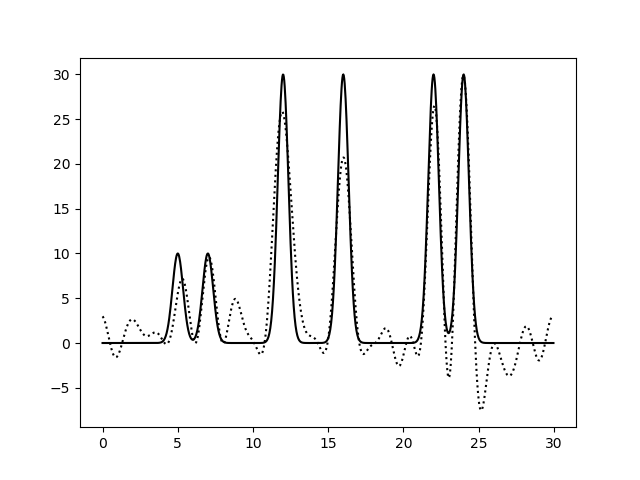
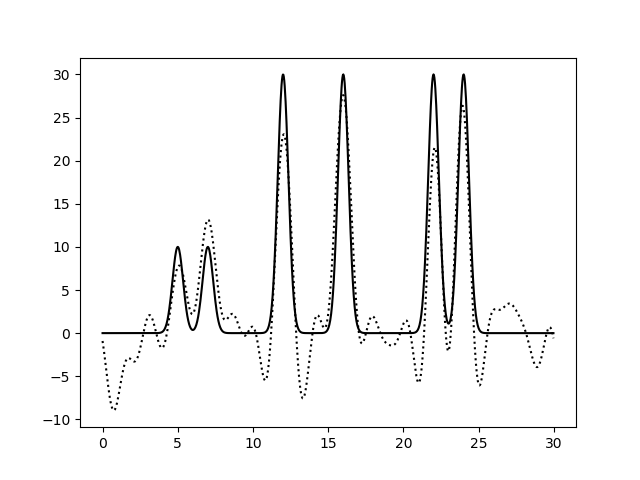
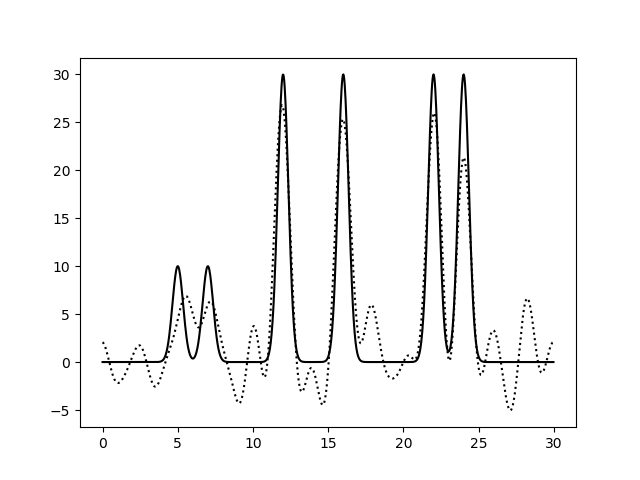
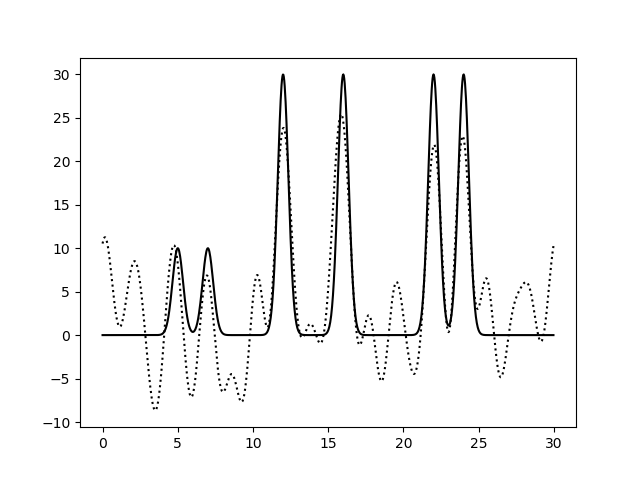
Варьирование этих парамеров показало (см рис 8-13), что для точности восстановления исходной функции более принципиально отсутствие шумов в фазах, а не в амплитудах.

Рисунок 8. Гармоники от 0-й до 20-й, F=0, P=0. Рисунок 9. Гармоники от 0-й до 20-й, F=20, P=0. Рисунок 10. Гармоники от 0-й до 20-й, F=0, P=20.

Рисунок 11. Гармоники от 0-й до 20-й, F=20, P=20. Рисунок 12. Гармоники от 0-й до 20-й, F=40, P=0. Рисунок 13. Гармоники от 0-й до 20-й, F=0, P=40.

Восстановление исходной функции ЭП по неполному набору гармоник

Так как в реальном эксперименте не всегда можно найти полный набор гармоник, рассмотрим, насколько хорошо восстанавливается исходная функция ЭП по неполному набору.

Процедура выполнения вычислений стандартная, поочередно отфильтрованы гармоники с самым маленьким, средним и самым большим разрешением (а именно с 0-й по 7-ю, с 7-й по 13-ю и с 13-й по 20-ю).

Хуже всего выглядит набор, у которого удалены центральные гармоники, по нему не возможно установить положение атомов. Наборы с маленьким размерешения нужны для "придания формы" функции, то есть без них восстановленная фукнция "плывет". Лучше всего восстановилась функция по 1-13 гармоникам - она просто слегка нечеткая.

python func2fourier.py func.txt
python fourier-filter.py func_ft.txt -r 0-7,13-20
python fourier2func.py func_ft_filtered.txt

Результат представлен на рисунках 14-16.

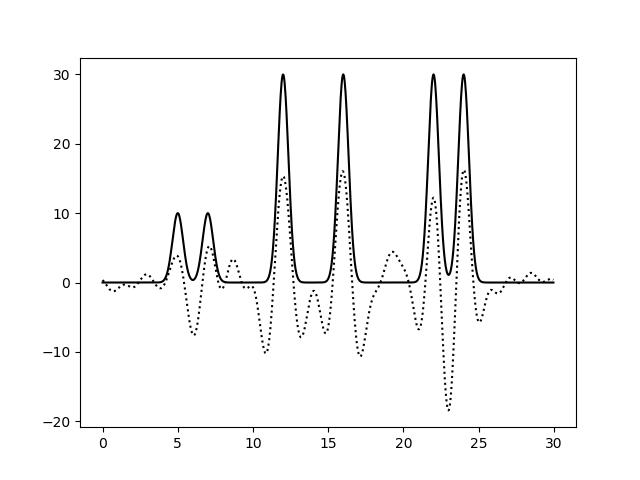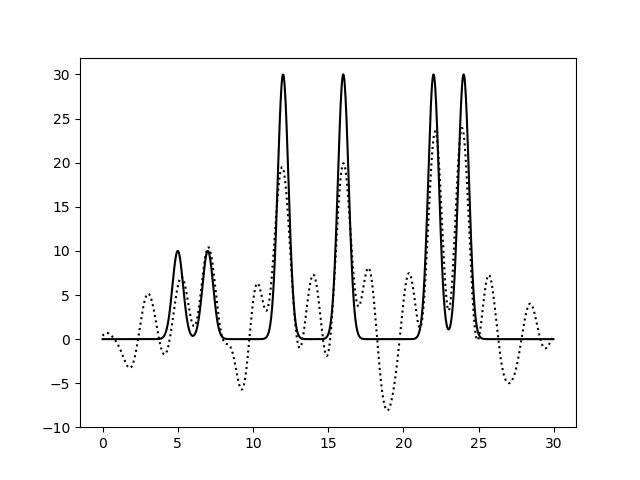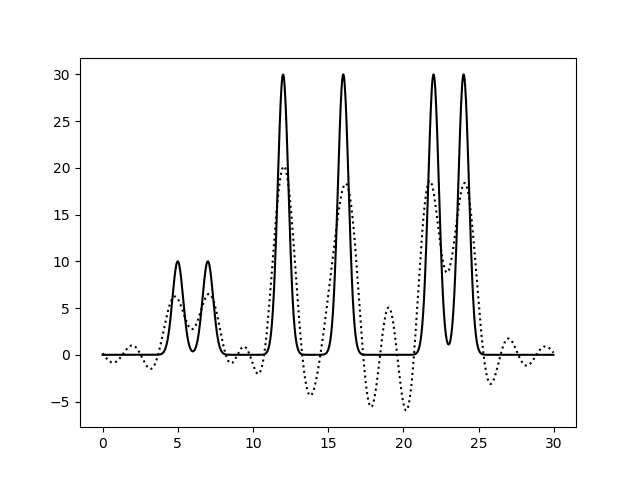Рисунок 14. Гармоники от 7-й до 20-й. Рисунок 15. Гармоники от 0-й до 7-й и от 13-й до 20-й. Рисунок 16. Гармоники от 0-й до 13-й.

Итоговая таблица

Разрешение - длина отрезка/номер гармоники. Полнота - количество гарминик в неполном наборе/количество гармоник в полном наборе.

Набор Гармоник Разрешение (A) Полнота (%) Шум Амплитуд (%) Шум Фаз (%) Качество разрешения Комментарий

Полный набор гамоник

0-5 6 100 0 0 Плохое

0-10 3 100 0 0 Среднее

0-15 2 100 0 0 Хорошее

0-20 1.5 100 0 0 Отличное Оптимальное количество гармоник.

0-27 1.1 100 0 0 Отличное Почти-почти идеально.

0-30 1 100 0 0 Отличное Идеально.

Полный набор гамоник, добавление гауссовского шума

0-20 1.5 100 0 20 Хорошее Больша шума и один пик несколько смещён.

0-20 1.5 100 0 40 Среднее Угадываются 4 пика из 6. Много шума, два пика неотличимы от шума..

0-20 1.5 100 20 0 Отличное Пики довольно четкие.

0-20 1.5 100 40 0 Хорошее Пики расширены, сливаются.

0-20 1.5 100 20 20 Отличное Много шума, но положение и примерный размер всех пиков отпереляются довольно точно.

Неполный набор гамоник

7-20 1.5 65 0 0 Среднее Не угадывается общее очертание функции. Положение некоторых атомов определить можно, но не все.

0-7, 13-20 1.5 70 0 0 Среднее Возможно опредеить положение некоторых атомов, тогда как пики других смещены и/или не отличимы от шума.

0-13 2.3 65 0 0 Хорошее Пики менее четкие, сливаются. Тем не менее, зная количество атомов, можно определить их положение.


Рисунок 2. Гармоники от 0-й до 5-й.	Рисунок 3. Гармоники от 0-й до 10-й.	Рисунок 4. Гармоники от 0-й до 15-й.

Рисунок 5. Гармоники от 0-й до 20-й.	Рисунок 6. Гармоники от 0-й до 27-й.	Рисунок 7. Гармоники от 0-й до 30-й.


Рисунок 8. Гармоники от 0-й до 20-й, F=0, P=0.	Рисунок 9. Гармоники от 0-й до 20-й, F=20, P=0.	Рисунок 10. Гармоники от 0-й до 20-й, F=0, P=20.

Рисунок 11. Гармоники от 0-й до 20-й, F=20, P=20.	Рисунок 12. Гармоники от 0-й до 20-й, F=40, P=0.	Рисунок 13. Гармоники от 0-й до 20-й, F=0, P=40.


Рисунок 14. Гармоники от 7-й до 20-й.	Рисунок 15. Гармоники от 0-й до 7-й и от 13-й до 20-й.	Рисунок 16. Гармоники от 0-й до 13-й.

Набор Гармоник	Разрешение (A)	Полнота (%)	Шум Амплитуд (%)	Шум Фаз (%)	Качество разрешения	Комментарий
Полный набор гамоник
0-5	6	100	0	0	Плохое
0-10	3	100	0	0	Среднее
0-15	2	100	0	0	Хорошее
0-20	1.5	100	0	0	Отличное	Оптимальное количество гармоник.
0-27	1.1	100	0	0	Отличное	Почти-почти идеально.
0-30	1	100	0	0	Отличное	Идеально.
Полный набор гамоник, добавление гауссовского шума
0-20	1.5	100	0	20	Хорошее	Больша шума и один пик несколько смещён.
0-20	1.5	100	0	40	Среднее	Угадываются 4 пика из 6. Много шума, два пика неотличимы от шума..
0-20	1.5	100	20	0	Отличное	Пики довольно четкие.
0-20	1.5	100	40	0	Хорошее	Пики расширены, сливаются.
0-20	1.5	100	20	20	Отличное	Много шума, но положение и примерный размер всех пиков отпереляются довольно точно.
Неполный набор гамоник
7-20	1.5	65	0	0	Среднее	Не угадывается общее очертание функции. Положение некоторых атомов определить можно, но не все.
0-7, 13-20	1.5	70	0	0	Среднее	Возможно опредеить положение некоторых атомов, тогда как пики других смещены и/или не отличимы от шума.
0-13	2.3	65	0	0	Хорошее	Пики менее четкие, сливаются. Тем не менее, зная количество атомов, можно определить их положение.