Филогенетические деревья. Занятие 3

1. Укоренение в среднюю точку

При выполнении задания 4 предыдущего занятия методом Neighbour Joining построено 2 неукорененных филогенетических дерева. 2 укорененных дерева были получены методом UPGMA (Unweighted Pair Group Method with Arithmetic Mean - Average Distance в JalView). Оба метода принимают на вход матрицу расстояний.

Чтобы укоренить в среднюю точку деревья, построенные методом Neighbour Joining, воспользуюсь программой retree пакета PHYLIP. Для этого: копирую файл retree.exe с диска P в свою рабочую директорию; копирую файл с деревом в Newick-формате в файл с именем intree без расширения; запускаю retree и укорененяю в среднюю точку - M ("Midpoint root the tree").

Neighbour Joining Using % Identity

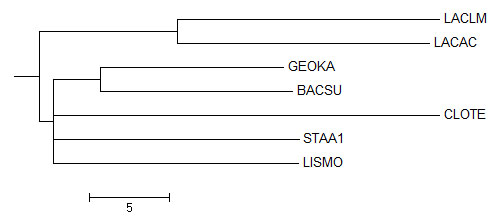
Укорененное в среднюю точку - rootnjuident.tre и неукорененное деревья соответственно

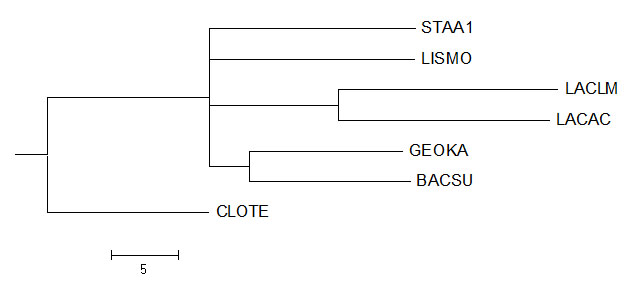
Правильное дерево:

Приведенное филогенетическое дерево неверно. Укоренение в ветвь CLOTE оказалось бы более правильным.

В данном случае уже неукорененное дерево отличалось от исходного наличием ветвей {LACLM, LACAC, GEOKA, BACSU} против {STAA1, LISMO, CLOTE}, {LISMO, LACLM, LACAC, GEOKA, BACSU} против {STAA1, CLOTE} и отсутствием {BACSU, GEOKA, LISMO} против {CLOTE, LACAC, LACLM, STAA1}, {BACSU, GEOKA, LISMO, STAA1} против {CLOTE, LACAC, LACLM}.

Neighbour Joining Using BLOSUM62

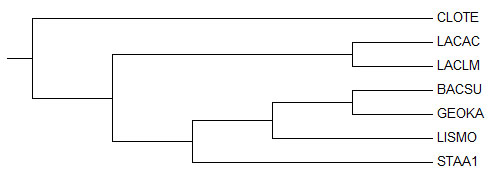
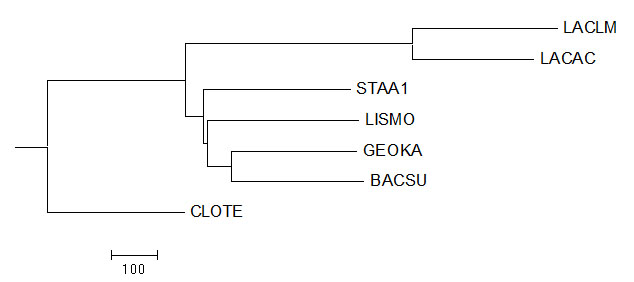
Укорененное в ветвь {LACAC, LACLM} против {CLOTE, BACSU, GEOKA, LISMO, STAA1} дерево - rootnjublos.tre и неукорененное дерево соответственно

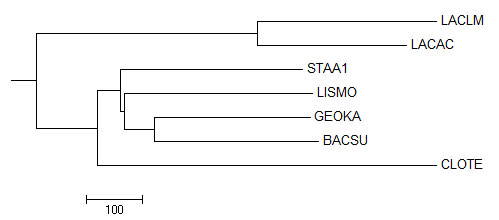
Правильное дерево:

Неукорененное дерево имело те же ветви, что и правильное. Но укорененное дерево было бы более похоже на исходное, если бы корень пришелся на ветвь CLOTE.

2. Использование внешней группы

Деревья, построенные методом максимальной экономии ("Maximum parsimony") невозможно укоренить в среднюю точку, из-за того, что метод не реконструирует длины ветвей. Можно воспользоваться укоренением с помощью внешней группы.

Реконструирую методом максимальной экономии укорененное дерево отобранных бактерий, используя в качестве внешней группы белок того же семейства из кишечной палочки (Escherichia coli, ECOLI). Для этого добавляю к файлу с невыровненными последовательностями белка фактора элонгации трансляции Ts (EFTS) фирмикут последовательность белка из кишечной палочки, после чего выравниваю их вместе, снова используя Muscle with Defaults. Получаю seq2al.fasta.

Результат импортирую в программу MEGA. В меню Subtree выбираю Root и указываю в качестве корня ветвь, ведущую к ECOLI. Чтобы получить изображение укоренённого дерева без ECOLI, использую "Show Subtree Separately".

Изображение укоренённого дерева

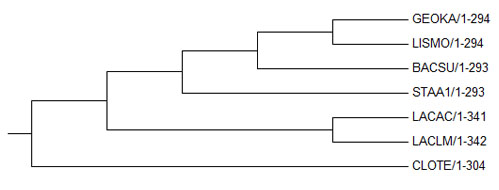
Укоренение пришлось на ветвь CLOTE - я считаю его правильным. Получилось аналагичное исходному дерево.

3. Бутстреп

Провожу бутстрэп-анализ филогении моих белков, используя один из методов, доступных из программы MEGA - Neighbour Joining. В окошке, которое открывается после вызова программы, в меню "Test of Phylogeny" выбираю "Bootstrap method". Указываю число реплик, равное 100. Каждая бутстрэп-реплика получается в результате случайного удаления половины столбцов из выравнивания с заменой их копиями других (тоже случайно выбранных) столбцов.

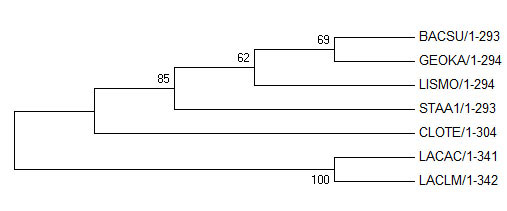
Original tree

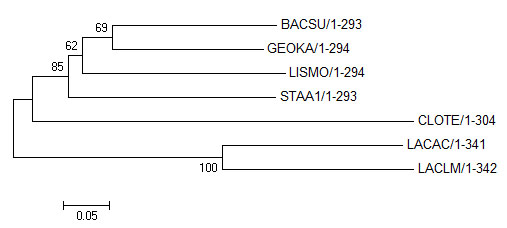
Bootstrap consensus tree

Видно, что деревья, "Original tree" и "Bootstrap consensus tree" не отличаются. Полученные деревья имеют те же нетривиальные ветви, что и правильное дерево, от которого они отличаются лишь укоренением. Исходное дерево укоренено по CLOTE, полученные - по ветви {LACAC, LACLM} против {CLOTE, BACSU, GEOKA, LISMO, STAA1}.

Правильные ветви имеют высокую поддержку. Чем число ближе к 100, тем правильнее ветвь, так, ветвь {LACAC, LACLM} против {CLOTE, BACSU, GEOKA, LISMO, STAA1} с числом 100 воспроизводилась всеми испробованными на занятии 2 методами.

Неправильные ветви имеют меньшую поддержку. Например, сравнивая между собой, ветви {BACSU, GEOKA, LISMO} против {CLOTE, LACAC, LACLM, STAA1} - 62 и {BACSU, GEOKA, LISMO, STAA1} против {CLOTE, LACAC, LACLM} - 85, замечаю, что при выполнении занятия 2 первая ветвь отсутствовала 2 раза из четырех, вторая - один. Таким образом, вторая ветвь более правильная и именно ей соответствует большее число.