Анализ результатов моделирование самосборки липидного бислоя

Визуальный анализ движений молекул

Для получения pdb-файла была использована команда:

При вопросе о выводке групп выбрано DPPC.

Был проведен визуальный анализ анимации. Нечто похожее на бислой с гидрофильными группами смотрящими наружу и гидрофобными - внутрь формируется уже на 10-м кадре (t=4500). Cо временем бислой становится более плоским и отчетливым и почти перестает уплощаться к 70-му кадру (t=34500) (рис. 1).

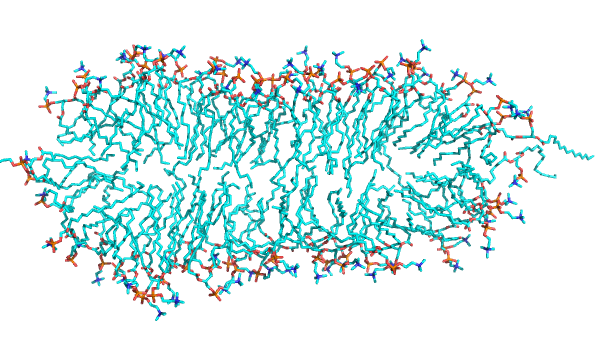
Рис. 1. 70-ый кадр.

Определение площади, занимаемой одним липидом

Получены размеры ячейки из траектории:

Ось y является нормалью к поверхности бислоя. Зависимость площади по соотвествующим осям (не нормали к поверхности бислоя) от времени представлена на рис. 2. Полученное значение площади, занимаемой одним липидом в слое, равно 0,74 нм (использовалось то, что в ячейке 32 липида в слое).

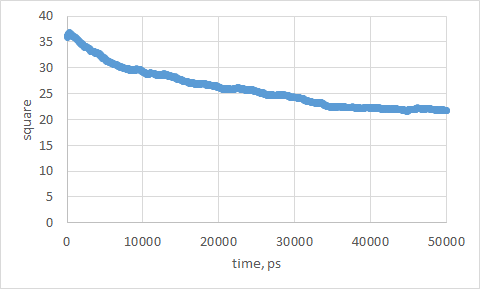
Рис. 2. Зависимость площади от времени.

Изменение гидрофобной и гидрофильной поверхностей в ходе самосборки

Построена зависимость изменения гидрофобной и гидрофильной поверхностей доступных растворителю от времени (рис. 3). Уменьшение гидрофобной поверхности, доступной растворителю, дает выигрыш в энергии и приводит к сборке липидов в бислой.

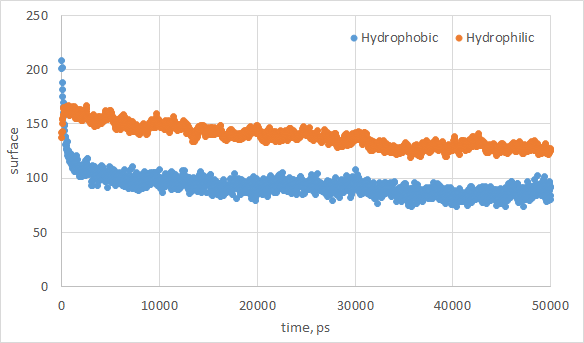
Рис. 3. Зависимость изменения гидрофобной и гидрофильной поверхностей доступных растворителю от времени.

Мера порядка

Традиционной мерой оценки фазового состояния бифильных молекул является мера порядка. Для анализа был скачен специальный индекс файл. Был запущен анализ. Для конца траектории:

Для начала траектории:

Построенные зависимости представлены на рис. 4 и 5. Видно возрастающий характер графиков как для конца, так и для начала траектории. При этом для конца траектории значения на порядок больше.

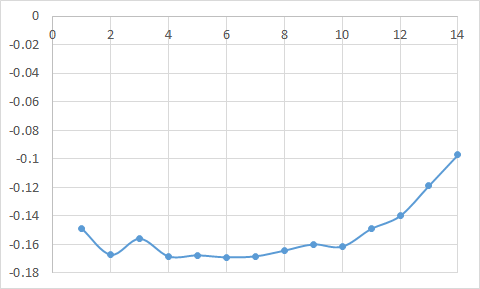
Рис. 4. Зависимость для конца траектории.

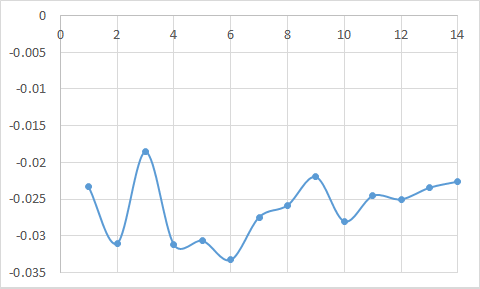
Рис. 5. Зависимость для начала траектории.

Основные сведения о работе

Силовое поле используемое при построении топологии - ffgmx.
Заряд системы - 0.
Размер и форма ячейки - 5,46 х 3,64 x 4,98 (в нм), параллелепипед.

Минимизация энергии:
Алогритм минимизации энергии - l-bfgs.
Алгоритм расчёта электростатики и Ван-дер-Ваальсовых взаимодействий - сut-off.
Модель, которой описывался растворитель - spc.

Утряска растворителя:
Число шагов - 10000.
Длина шага - 0,001 ps.
Алгоритм расчёта электростатики - pme, Ван-дер-Ваальсовых взаимодействий - сut-off.
Алгоритм термостата - Berendsen, баростата - no.

Основной расчёт МД:
Количество процессоров - 16.
Длина траектории - 50 ns.
Число шагов - 10000000.
Длина шага - 0,005 ps.
Алгоритм интегратора - md.
Алгоритм расчёта электростатики - pme, Ван-дер-Ваальсовых взаимодействий - cut-off.
Алгоритм термостата - v-rescale, баростата - Berendsen.