Восстановление электронной плотности |
Назад |
python compile-func.py -g 30,2.5,8+20,4,9+10,3,10.4+30,1,13.8+30,1.6,15+20,1,16.5
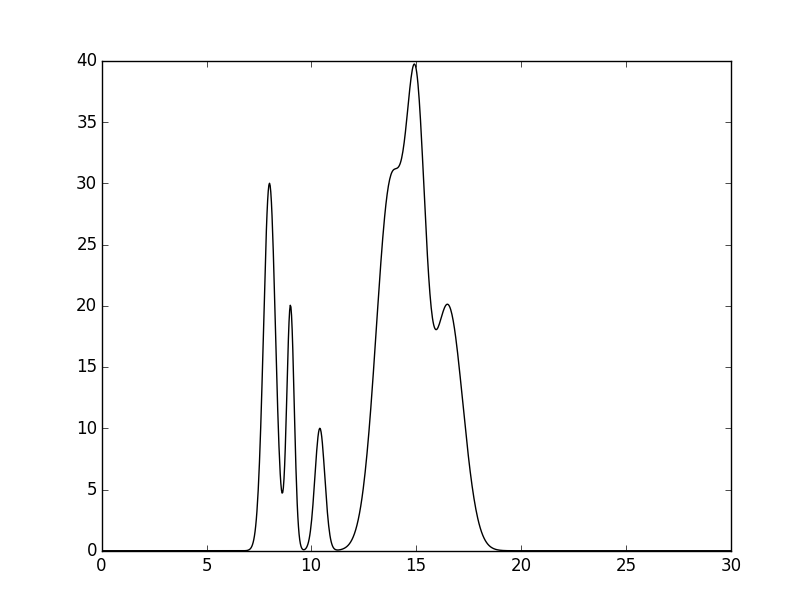 |
Параметры намеренно подбирались таким образом, чтобы в молекуле одни атомы были легко различимы, когда другие образуют общее, практически единое электронное облако.
В данном примере минимальное расстояние между пиками – 1А. По телеграфной теореме для восстановления исходного графика достаточно разложение на гармоники с разрешением менее 2А. Однако 4 и 5 пики довольно широкие, хотя и отстоят на 1.5А друг от друга, и возможно, даже при такой частоте их не удастся различить.
Проверим, сколько гармоник, полученных при помощи скрипта func2fourier.py достаточно, чтобы восстановить график с рис.1
python func2fourier.py -F 0 -P 0 python fourier-filter.py -r 0-15 python fourier2func.py -o no_noise_1-15.txtПри использовании первых 16 гармоник фон выражен слабо и можно различить 4 из 6 пиков. Разрешение этого фурье-синтеза, по условиям задания, составляет 2А.
При использовании первых 31 гармоник картина исходная картина восстанавливается отлично.
В промежуточном варианте с разрешением 1.5А (21 гармоника) можно даже различить слившиеся пики 4 и 5. Но пики 1 и 2 сливаются в один, несмотря на то что исходно они были раздельны – такое разрешение оказалось недостаточным для разделения пиков на расстоянии 1А. (см.рис.2)
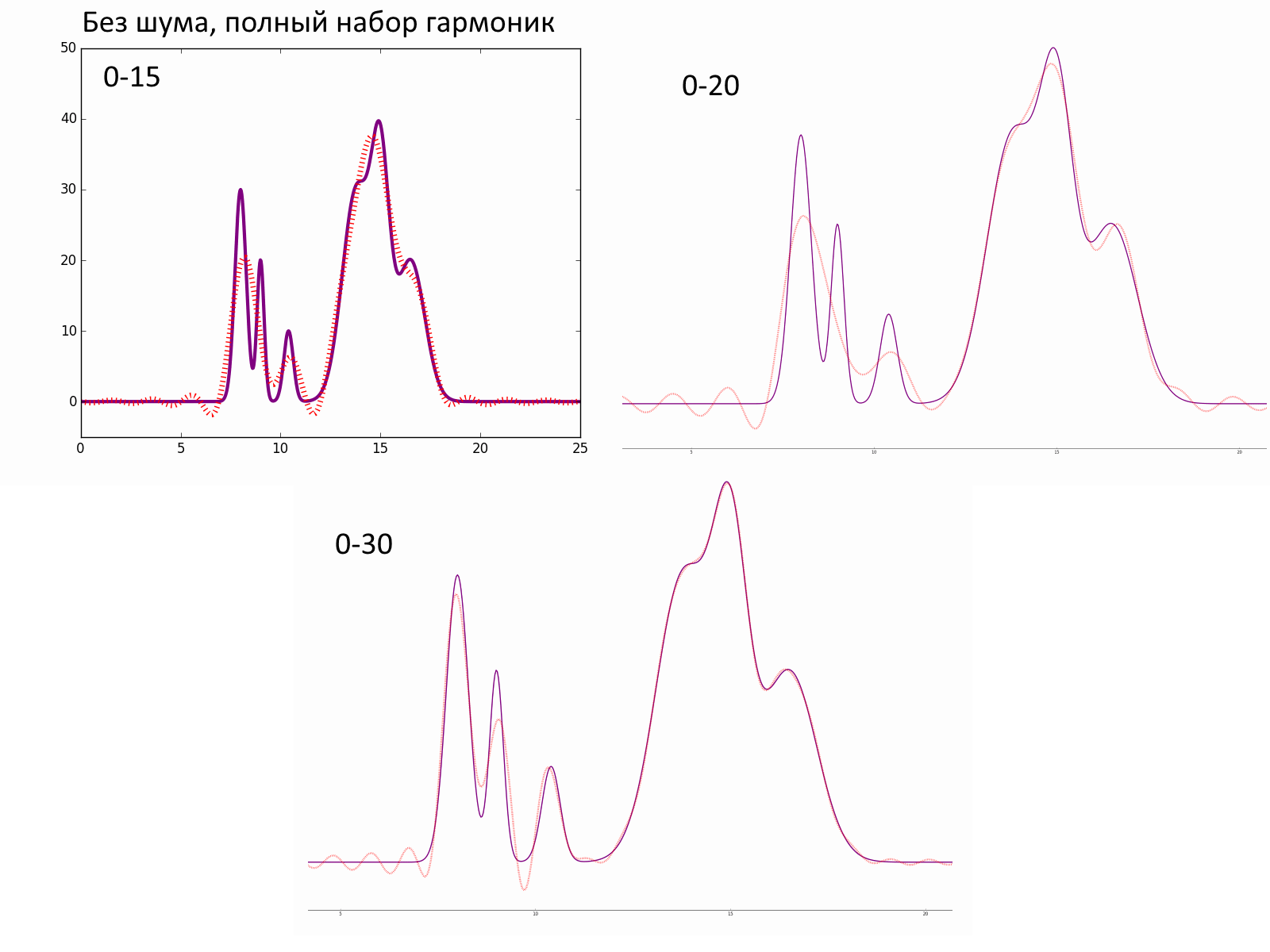
Рис.2 — восстановление ЭП полным набором гармоник в отсутствие шума.
Теперь проверим, насколько точными останутся результаты при внесении шума.
При уровнях шума 5%-10% по амплитуде и фазе сигнала результат практически не отличается от случая без шума. При уровне шума 20%-30% по обоим параметрам узнавание исходных пиков превращается в особое искусство. При более высоких помехах восстановленная функция уже не несёт никакой информации.
Из серии Фурье-синтезов с помехами только в одном параметре видно, что шум в R сильнее искажает картину, чем шум в F.(см.рис.3)
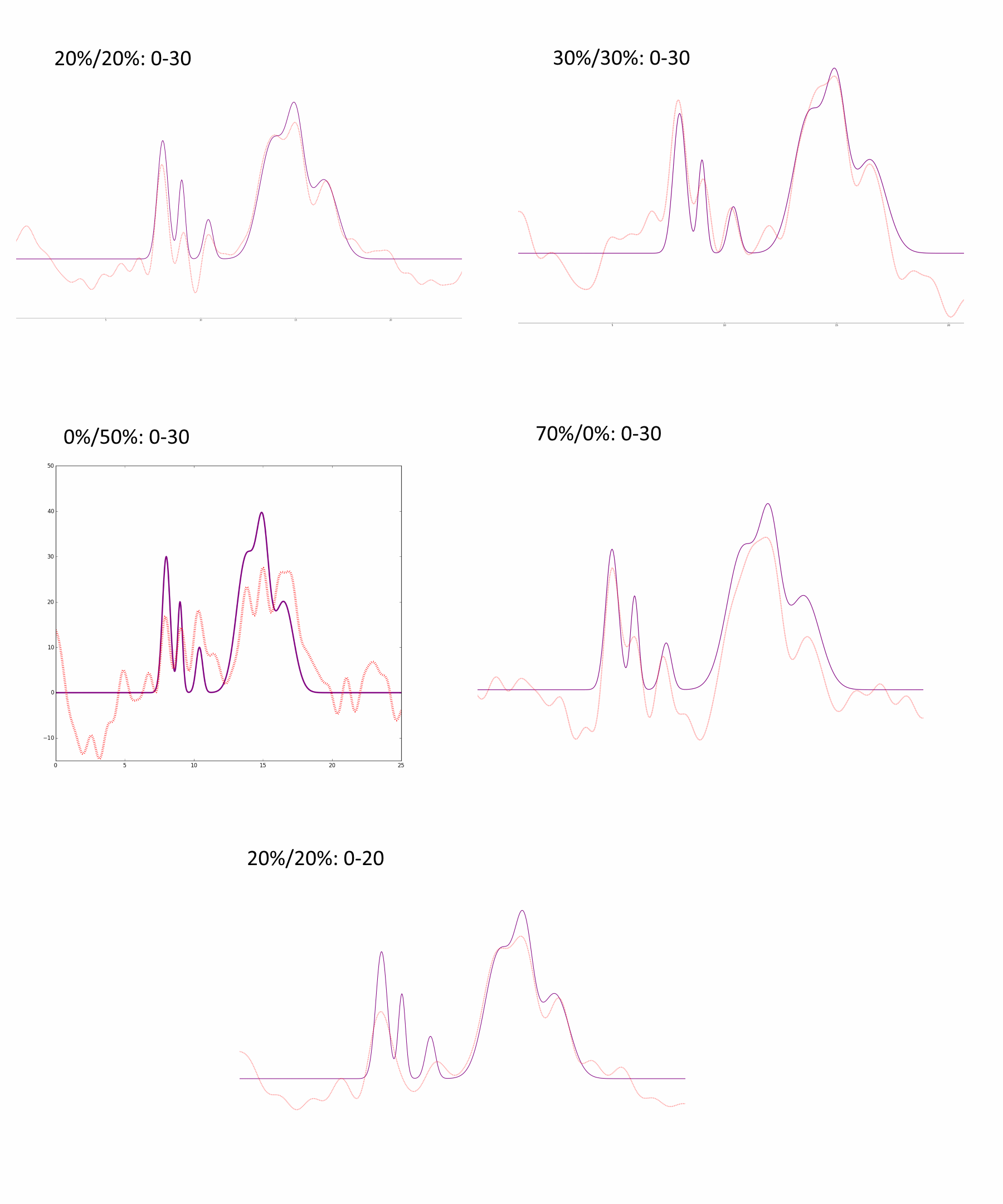
Рис.3 — восстановление ЭП полным набором гармоникпри наличии шума (первое число — % шума в параметре F, второе — в параметре R).
Обработка неполнх наборов гармоник показала, что невозможно восстановить ЭП, не зная гармоник низкого порядка. В то же время гармоники высокого порядка можно пропускать практически безболезненно.(см.рис.4)
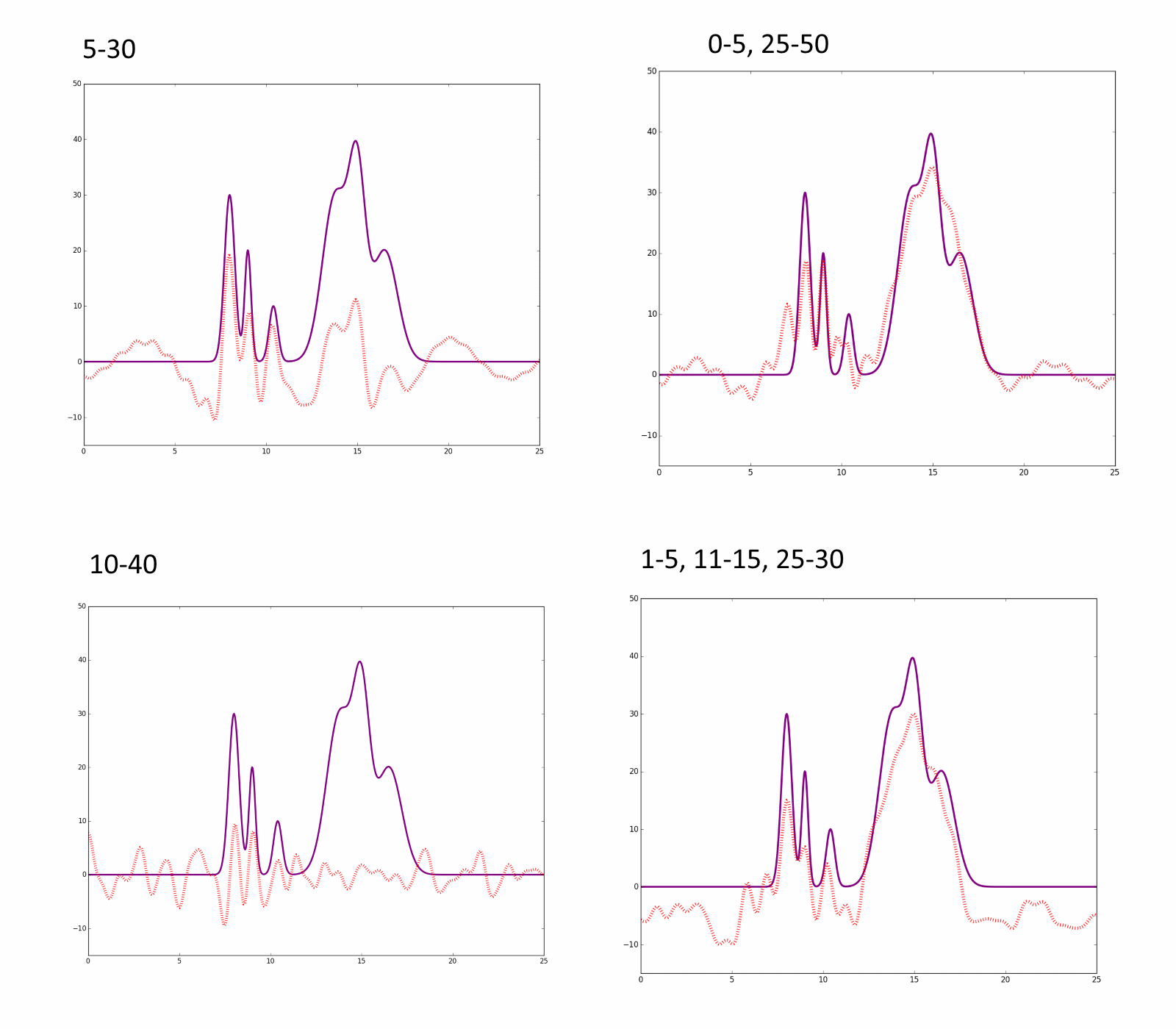
Рис.4 — синтез Фурье по неполному набору гармоник. Использованные в синтезе гармоники обозначены числами.
|
Набор гармоник |
Разрешение (Å) |
Полнота данных (%) |
Шум амплитуды (% от величины F) |
Шум фазы (% от величины phi) |
Качество восстановления (отличное, хорошее, среднее, плохое) |
|
Полный набор гармоник |
|||||
|
0-15 |
2A |
100% |
0 |
0 |
Средне |
|
0-30 |
1А |
100% |
0 |
0 |
Отлично |
|
0-20 |
1.5А |
100% |
0 |
0 |
Хорошо |
|
-//- x3 |
-//- x3 |
100% |
5 |
5 |
-//- x3 |
|
0-20 |
1.5А |
100% |
10 |
10 |
Средне |
|
0-30 |
1А |
100% |
10 |
10 |
Отлично |
|
0-20 |
1.5А |
100% |
20 |
20 |
Средне |
|
0-30 |
1А |
100% |
20 |
20 |
Отлично |
|
0-30 |
1А |
100% |
30 |
30 |
Средне |
|
0-15 |
2А |
100% |
50 |
0 |
Плохо |
|
0-30 |
1А |
100% |
50 |
0 |
Средне |
|
0-30 |
1А |
100% |
70 |
0 |
Средне |
|
0-15 |
2А |
100% |
0 |
50 |
Плохо |
|
0-30 |
1А |
100% |
0 |
70 |
Плохо |
|
0-30 |
1А |
100% |
0 |
50 |
Плохо |
|
Неполный набор гармоник |
|||||
|
10-40 |
0.75А |
76% |
0 |
0 |
Ужасно |
|
1-30 |
1А |
97% |
0 |
0 |
Хорошо |
|
5-30 |
1А |
81% |
0 |
0 |
Плохо |
|
1-5, 11-15, 25-30 |
1А |
52% |
0 |
0 |
Плохо |
|
0-5, 25-50 |
0.6А |
64 |
0 |
0 |
Плохо |
|
5-40 |
0.75 |
88% |
0 |
0 |
Плохо |
Табл.1 — результаты Фурье-синтезов с разными параметрами скриптов