Восстановление электронной плотности

1. Создание модельной функции ЭП в одномерной элементарной ячейке

Модель для компьютерного эксперимента. На отрезке [0,30] (ангстремы) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Электронные плотности (ЭП) атомов описываются гауссовой кривой. Взяли 2 молекулы: одна - 3 атома, другая - 2 атома.

Создадим функцию с помощью скрипта compile-func.py, команда:

С:\Python27\python compile-func.py -g 35,3,4.2+37,3,6.9+3,3.5,8.2+32,3,13.5+3,3.5,17.4

Мы получаем изображение нашей функции (рис.1) и файл func.txt.

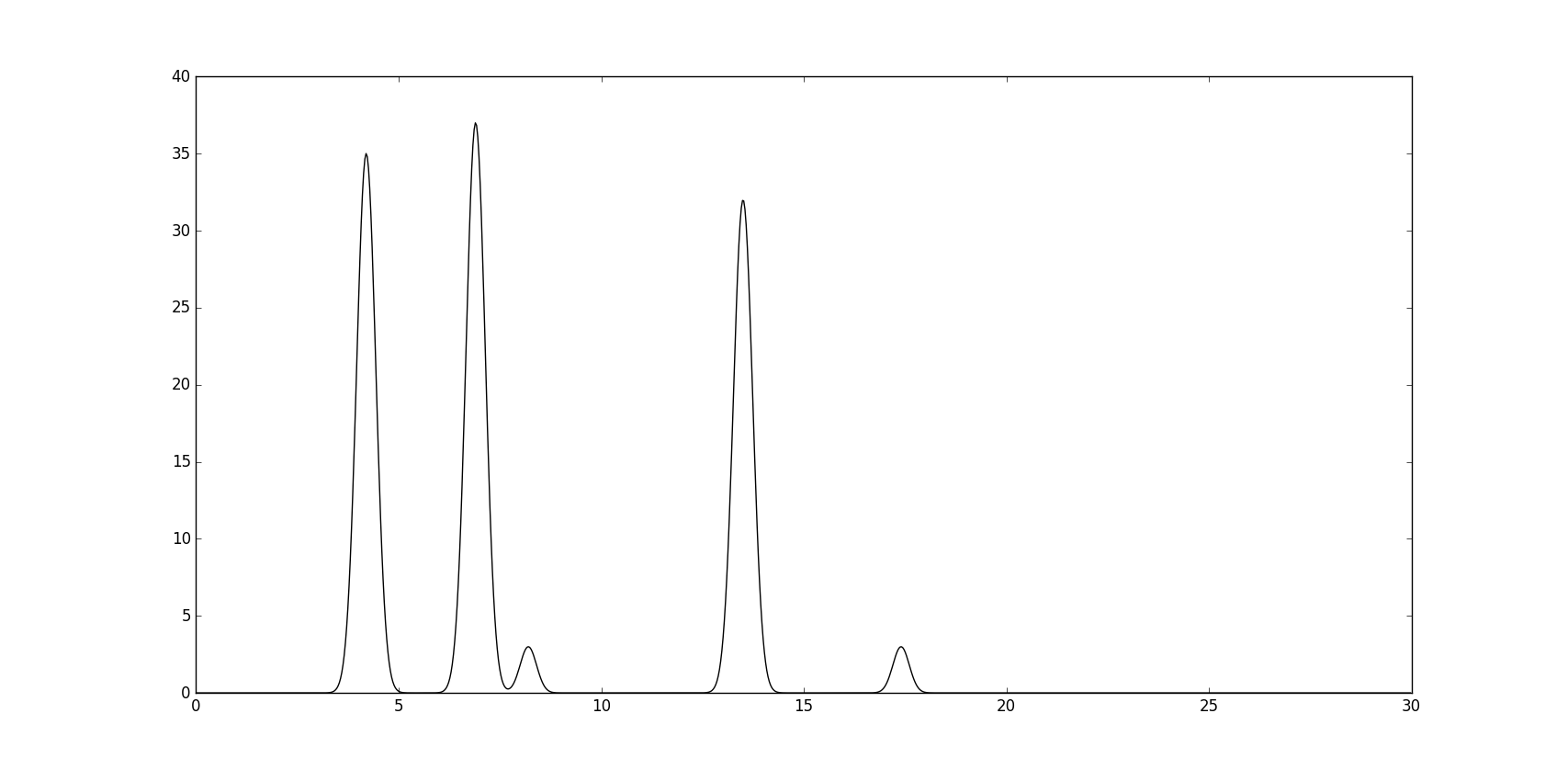
Рис.1. График функции.

2. Расчеты для полного набора гармоник.

Коэффициенты Фурье рассчитаем с помощью следующей команды:

С:\Python27\python func2fourier.py -i func.txt

Полученный файл: func_ft.txt. Он содержит амплитуды, фазы и номера гармоник. Всего их получилось 498.

Отбор гармоник проведем следующим образом:

C:\Python27\python fourier-filter.py -r 0-15 -i func_ft.txt -o func_ft_0-15.txt
C:\Python27\python fourier-filter.py -r 0-25 -i func_ft.txt -o func_ft_0-25.txt
C:\Python27\python fourier-filter.py -r 0-35 -i func_ft.txt -o func_ft_0-35.txt
C:\Python27\python fourier-filter.py -r 0-80 -i func_ft.txt -o func_ft_0-80.txt

C:\Python27\python fourier2func.py -f func.txt -i func_ft_0-15.txt -o two_func_0-15.txt
C:\Python27\python fourier2func.py -f func.txt -i func_ft_0-25.txt -o two_func_0-25.txt
C:\Python27\python fourier2func.py -f func.txt -i func_ft_0-35.txt -o two_func_0-35.txt
C:\Python27\python fourier2func.py -f func.txt -i func_ft_0-80.txt -o two_func_0-80.txt

Полученные результаты в виде наложения двух графиков (исходного для всех гармоник и для первых k) представлены на рис.2,3,4,5.

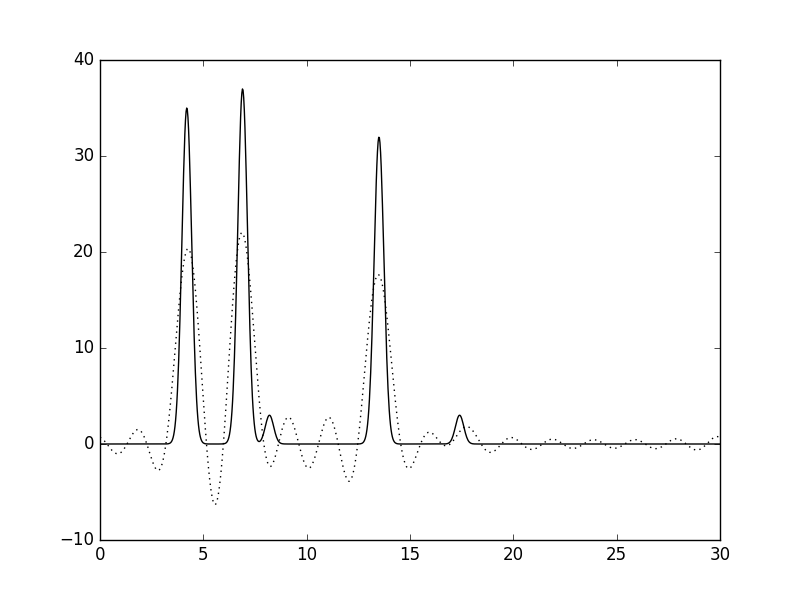Рис.2. Гармоники 0-15.	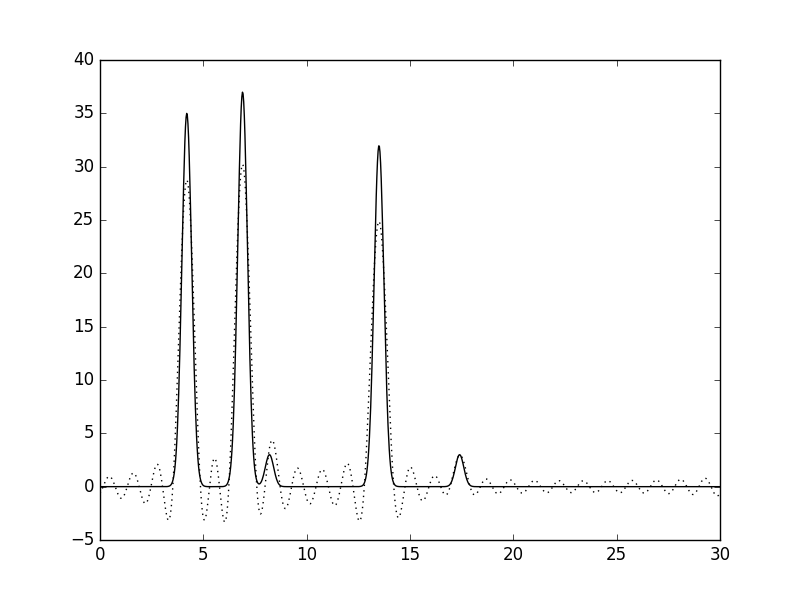Рис.3. Гармоники 0-25.
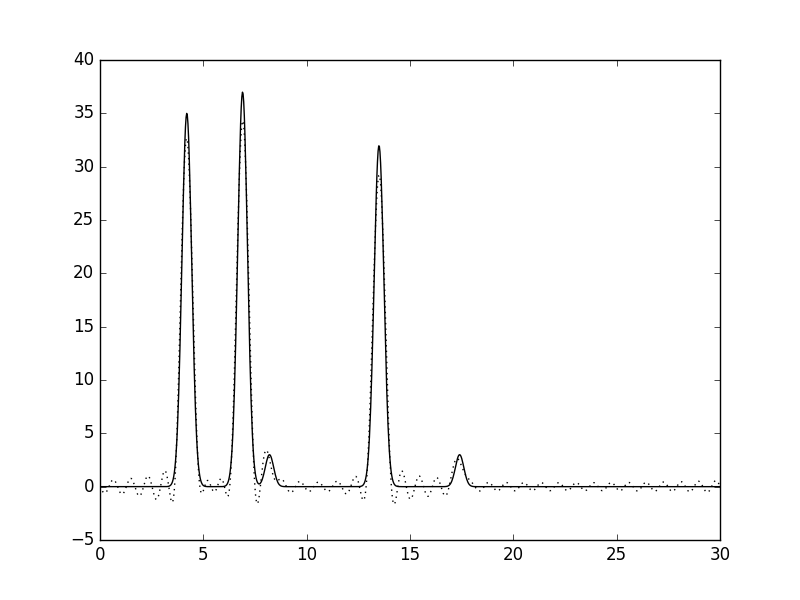Рис.4. Гармоники 0-35.	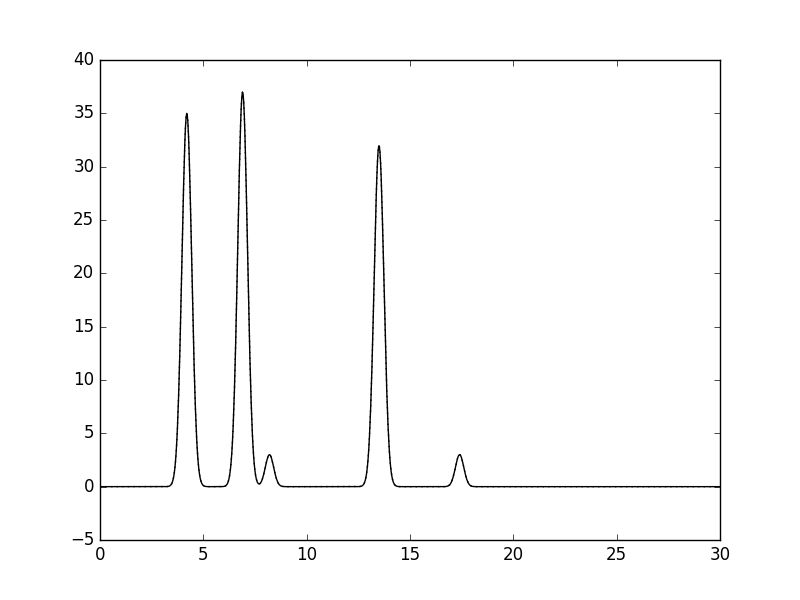Рис.5. Гармоники 0-80.

Таким образом, был найден n_0 (при котором восстановление отличное, т.е. можно найти положение максимумов гауссовых слагаемых по воссановленному графику по полному набору гармоник от 0 до n_0), он равен 35.
Сравним восстановленную фукнцию с исходной. При n=15 (рис.2) восстановление можно считать неудачным (плохое), т.к.положение не всех атомов можно установить четко. Для n=25 (рис.3) картина становится яснее (хорошее), однако все еще остается достаточного много "шума", поэтому, например, атом водорода легко с ним спутать. И, наконец, для n=35 (рис.4) уже можно сказать про "отличное восстановление". Также, была рассмотрена ситуация с n=80, при таком раскладе графики полностью совпали (рис.5).

Попробуем теперь добавить шум и посмотреть, что из этого получится. Для добавления гауссового шума к амплитудам и фазам воспользуемся следующими командами:

Шум к амплитуде в 20%:

C:\Python27\python func2fourier.py -F 20 -i func.txt -o ft_Anoise_20.txt
C:\Python27\python fourier-filter.py -r 0-35 -i ft_Anoise_20.txt -o ft_Anoise20_35.txt
C:\Python27\python fourier2func.py -i ft_Anoise20_35.txt -o Anoise_sum.txt

Шум к фазе в 20%:

C:\Python27\python func2fourier.py -P 20 -i func.txt -o ft_Fnoise_20.txt
C:\Python27\python fourier-filter.py -r 0-35 -i ft_Fnoise_20.txt -o ft_Fnoise20_35.txt
C:\Python27\python fourier2func.py -i ft_Fnoise20_35.txt -o Fnoise_sum.txt

Шум в 15% к амплитуде и фазе:

C:\Python27\python func2fourier.py -F 15 -P 15 -i func.txt -o ft_A_F_noise_15.txt
C:\Python27\python fourier-filter.py -r 0-35 -i ft_A_F_noise_15.txt -o ft_A_F_noise_35_15.txt
C:\Python27\python fourier2func.py -i ft_A_F_noise_35_15.txt -o A_F_noise_sum_15.txt

Шум в 5% к амплитуде и фазе:

C:\Python27\python func2fourier.py -F 5 -P 5 -i func.txt -o ft_A_F_noise_5.txt
C:\Python27\python fourier-filter.py -r 0-35 -i ft_A_F_noise_5.txt -o ft_A_F_noise_35_5.txt
C:\Python27\python fourier2func.py -i ft_A_F_noise_35_5.txt -o A_F_noise_sum_5.txt

На рис. 6 представлено прибавление шума к амплитуде в 20%, на рис.7 - к фазе в 20%, на рис.8 - к амплитуде и фазе в 15%, на рис.9 - к амплитуде и фазе в 5%. Восстановление проводилось по полному набору гармоник (от 0 до n_0=35). Таким образом, мы видим, что при наличии заметного шума (15-20%) качество восстановления можно считать "средним", поскольку нельзя однозначно установить все положения максимумов гауссовых функций. Однако, для 5% шума для амплитуд и фаз, восстановление можно назвать "хорошим".

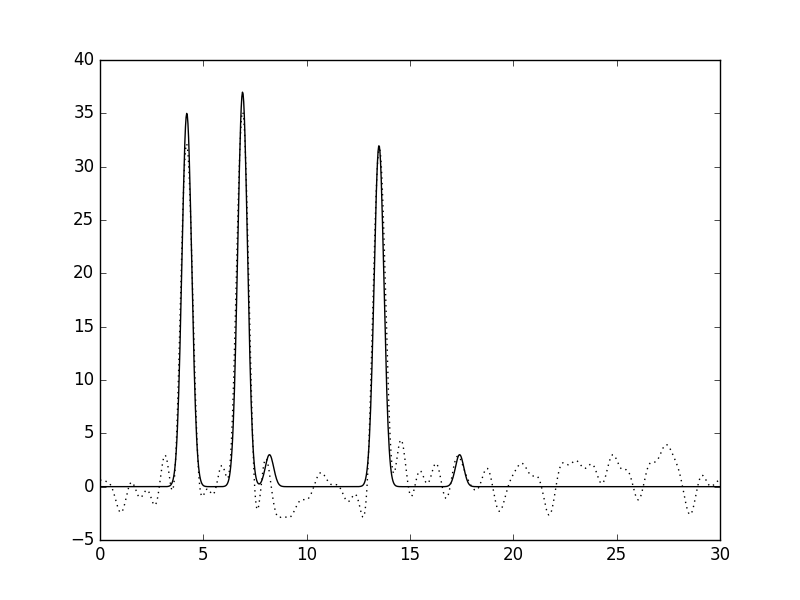Рис.6. Шум к амплитуде в 20%.	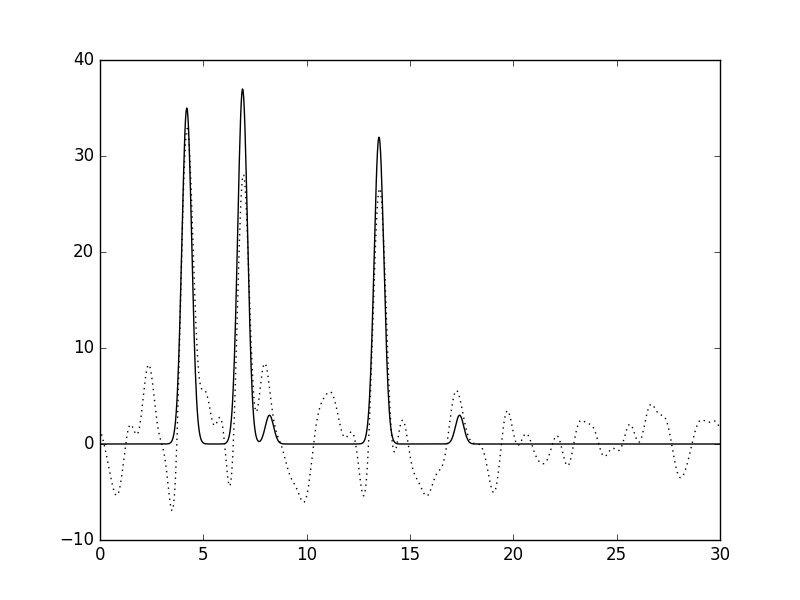Рис.7. Шум к фазе в 20%.
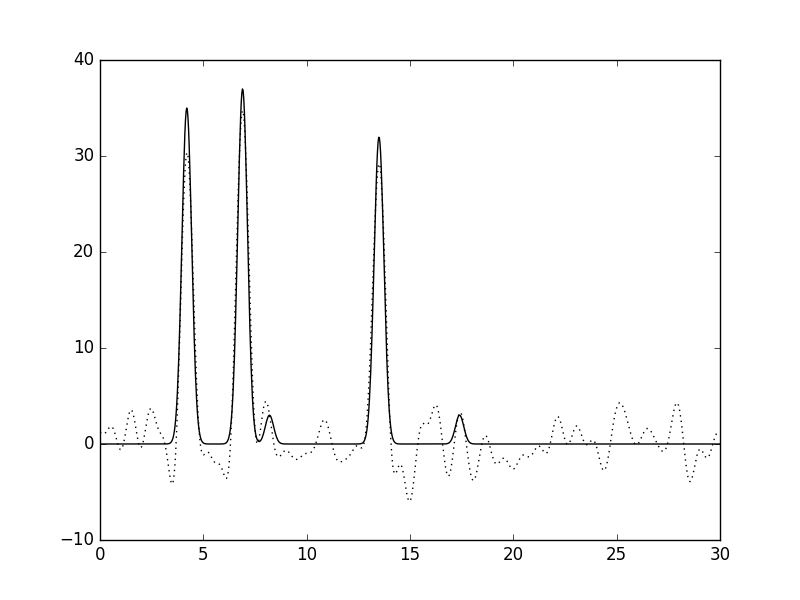Рис.8. Шум к амплитуде и фазе в 15%.	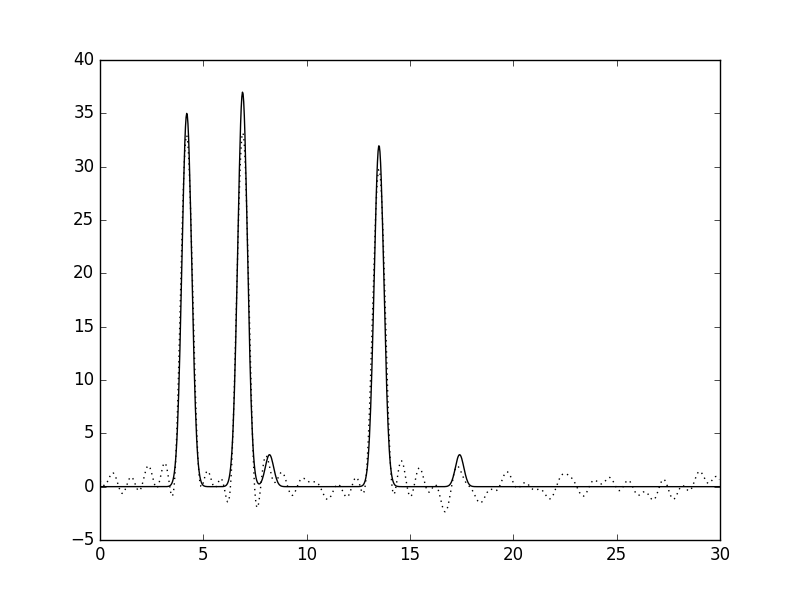Рис.9. Шум к амплитуде и фазе в 5%.

3. Расчет для неполного набора гармоник.

Для начала удалим одну и две первых гармоники, а затем несколько в середине и посмотрим, что из этого получится. Воспользуемся следующими командами:

Удалим первую гармонику: (n=0)

C:\Python27\python fourier-filter.py -r 1-35 -i func_ft.txt -o without_0.txt
C:\Python27\python fourier2func.py -i without_0.txt -o sum_1-35

Удалим первые две гармоники: (n=0,1)

C:\Python27\python fourier-filter.py -r 2-35 -i func_ft.txt -o without_01.txt
C:\Python27\python fourier2func.py -i without_01.txt -o sum_2-35.txt

Удалим 5% гармоник из середины набора (это 2 гармоники):

C:\Python27\python fourier-filter.py -r 0-17,19-35 -i func_ft.txt -o ft_exept2.txt
C:\Python27\python fourier2func.py -i ft_exept2.txt -o sum_exept2.txt

Удалим 14% гармоник из середины набора (это 6 гармоник):

C:\Python27\python fourier-filter.py -r 0-14,18-22,25-35 -i func_ft.txt -o ft_exept6.txt
C:\Python27\python fourier2func.py -i ft_exept6.txt -o sum_exept6.txt

Удаление первой гармоники (рис. 10)привело лишь к сдвигу по оси ординат, что очень даже логично, т.к. была исключено было значени F₀. Поскольку максимумы определяются замечательно, даем оценку восстановлению "отлично". Аналогичную оценку даем восстановленной функции без первых двух гармоник (рис. 11), несмотря на некоторое искажение.
В случае удаления гармоник из середины (рис.12, 5% и рис.13, 14%), качеству можно дать оценку "среднее", ибо максимумы еще можно угадать, зная их число. Однако, шум подступает, так сказать, к сигналу от атома.

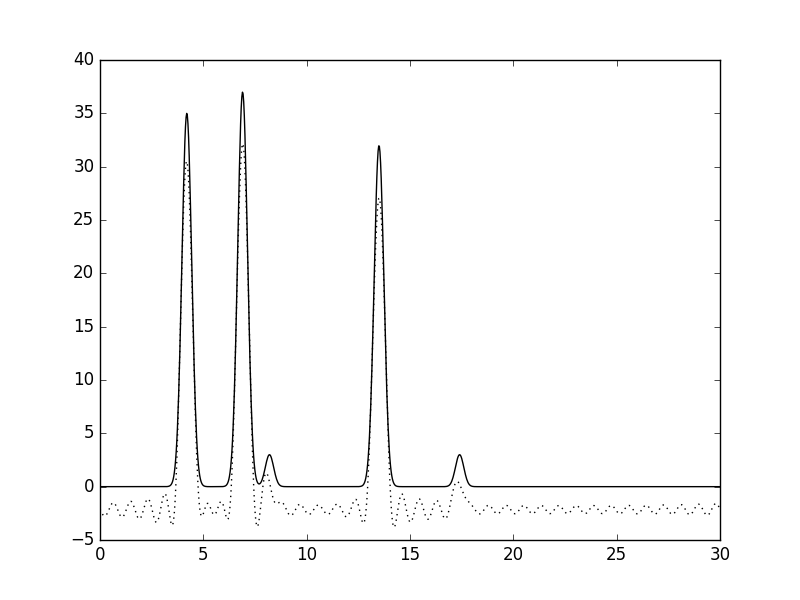Рис.10. Удаление первой гармоники.	Рис.11. Удаление первых двух гармоник.
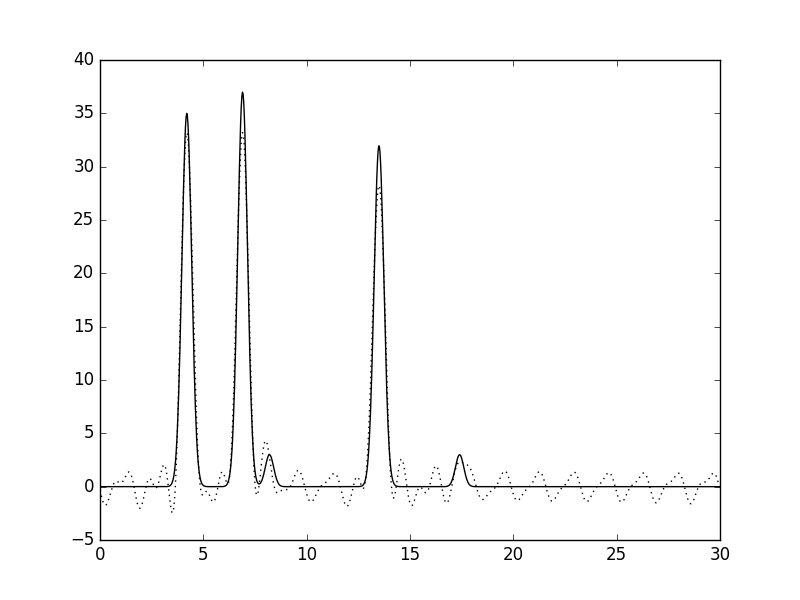Рис.12. Удаление 5% (2 гармоник) в середине.	Рис.13. Удаление 14% (6 гармоник) в середине.

Рассмотрим теперь добавление n_0+10, т.е. 45 гармоники. Воспользуемся следующими командами:

C:\Python27\python fourier-filter.py -r 0-35,45 -i func_ft.txt -o add.txt
C:\Python27\python fourier2func.py -i add.txt -o sum_add.txt

На рис.14 представлено добавление 45 гармоники. Как мы видим, добавление гармоники незначительно отразилось на функции, качество восстановления можно считать "отличным".

Рис.15. Добавление гармоники n=45.

Определение разрешения и полноты данных представлено в таблице: table.txt

Некоторые примечания по нахождению значений: для полного набора гармоник разрешение = 30Ангстрем/35 (период - расстояние между соседними максимумами синусоиды гармоники с наибольшим номером), полнота - 100%, т.к. она численно равна отношению гармоник в наборе, период которых не меньше разрешения к числу гармоник в полном наборе (и умножить на 100%). В случае набора гармоник 0,..., n, n+10 принималось разрешение для набора 0,..., n, а за полноту данных принималось 100%. Т.е. при указании разрешения для неполного набора гармоник желательно не превышать некоторое пороговое значение полноты данных, например, 90%.