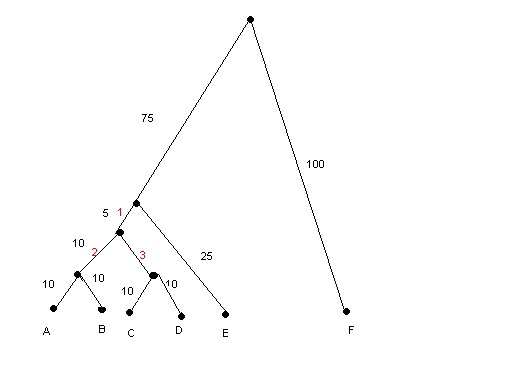
Задание 2. Описать ветви дерева как разбиения множества листьев (дерево считалось бескорневым). A B C D E F 1 * * * * . . 2 . . * * * * 3 * * . . * *
-
Задание 3. Получить искуственные мутантные последовательности, соответствующие листьям и узлам дерева,
считая, что в корне находится последовательность гена вашего белка.
-
Рассчетная формула: count=990*n/100
990- длина гена, n- колличество замен
Для получения "мутантов" была использована программа msbar пакета EMBOSS.
Скрипт:
msbar rpoa_gene.fasta F -point 4 -count 990 -auto
msbar rpoa_gene.fasta ABCDE -point 4 -count 743 -auto
msbar ABCDE E -point 4 -count 248 -auto
msbar ABCDE ABCD -point 4 -count 50 -auto
msbar ABCD AB -point 4 -count 99 -auto
msbar ABCD CD -point 4 -count 99 -auto
msbar AB A -point 4 -count 99 -auto
msbar AB B -point 4 -count 99 -auto
msbar CD C -point 4 -count 99 -auto
msbar CD D -point 4 -count 99 -auto
-
Задание 4. На основе последовательностей, соответствующих листьям, реконструировать дерево
алгоритмами UPGMA, Neighbor-joining и максимального правдоподобия.
-
Последовательности, соответствующие листьям были помещены в 1 файл ali.fasta.
Чтобы реконструировать дерево алгоритмом максимального правдоподобия, запустили программу fdnaml:
fdnaml ali.fasta -ttratio 1 -auto
В файле с расширением .dnaml - содержится схематичное изображение дерева и небольшое
текстовое описание(кладограмма):
+-B
|
| +------E
1--3
| | +-----------------------------------F
| +--4
| | +-D
| +--2
| +-C
|
+--A
Дерево неукорененное.
Between And Length Approx. Confidence Limits
------- --- ------ ------- ---------- ------
1 A 0.08324 ( 0.06280, 0.10368) **
1 B 0.06669 ( 0.04822, 0.08515) **
1 3 0.09000 ( 0.06626, 0.11374) **
3 E 0.20972 ( 0.17538, 0.24418) **
3 4 0.01852 ( zero, 0.03800) *
4 F 1.18861 ( 1.03204, 1.34519) **
4 2 0.05169 ( 0.03073, 0.07265) **
2 D 0.07257 ( 0.05333, 0.09188) **
2 C 0.08049 ( 0.06030, 0.10061) **
* = significantly positive, P < 0.05
** = significantly positive, P < 0.01
Для реконструкции дерева алгоритмами UPGMA или Neighbor-joining, пришлось посчитать попарные расстояния между
последовательностями программой fdnadist:
fdnadist ali.fasta -ttratio 1 -auto
Полученный файл mut .fdnadist был подан на вход программе fneighbor:
1) Для реконструкции алгоритмом Neighbor-joining:
fneighbor ali.fdnadist -auto
2) Для реконструкции алгоритмом UPGMA:
fneighbor ali.fdnadist -treetype u -auto
Программа UPGMA:
+-B
!
! +-C
! +-2
! +-3 +-D
! ! !
1--4 +-----E
! !
! +----------------------------------F
!
+--A
remember: this is an unrooted tree!
Between And Length
------- --- ------
1 B 0.07345
1 4 0.08991
4 3 0.00357
3 2 0.06628
2 C 0.07804
2 D 0.07473
3 E 0.21409
4 F 1.15539
1 A 0.07618
Neighbor-joining алгоритм:
+----A
+----1
! +----B
+-3
! ! +----C
+----------------------------4 +----2
! ! +----D
--5 !
! +----------E
!
+---------------------------------------F
From To Length Height
---- -- ------ ------
5 4 0.47673 0.47673
4 3 0.02998 0.50671
3 1 0.08022 0.58693
1 A 0.07482 0.66174
1 B 0.07482 0.66174
3 2 0.07865 0.58536
2 C 0.07639 0.66174
2 D 0.07639 0.66174
4 E 0.18501 0.66174
5 F 0.66174 0.66174
A B C D E F real Max UPGMA N-J
* * . . . . + + + +
. . * * . . + + + +
* * * * . . + - - +
. . * * * . - - + -
. . * * . * - + - -
Исходя из полученной таблицы больше всего на исходное дерево похоже дерево, полученное
программой N-J. Возможно, это связано с тем, что алгоритм N-J не учитывает теорию молекулярных
часов. Поэтому он и подходит для построения неультраметрических деревьев, у которых расстояния
от каждого листа до корня не равны между собой.
В то время как программа UPGMA работает с деревьями в соответствии с теорией молекулярных часов.
Исследуемое мной дерево не ультраметрическое, поэтому лучше всего справилась программа N-J.
На главную
страницу
©Фомичева Анастасия,2006