Сравнение разных способов оценки эволюционных расстояний между гомологичными нуклеотидными последовательностями

Нам нужно разобраться с границами применимости двух способов оценки расстояния, а именно: оценка расстояния как доли несовпадающих нуклеотидов и по методу Джукса-Кантора.
Вначале была построена матрица "истинных" попарных эволюционных расстояний в данной эволюционной модели. В ней приведены расстояния между всеми узлами филогенетического дерева (включая исходную последовательность гена ENO_ECOLI). Расстояния также взяты с дерева (определены как число мутаций, разделяющих последовательности, в пересчёте на 100 нуклеотидов).

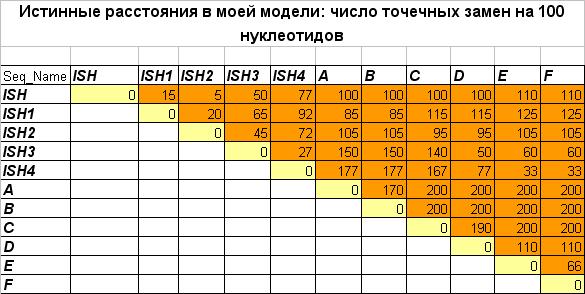
Обозначения последовательностей:
ISH — исходная последовательность гена;
ISH1...ISH4 — последовательности, находящиеся в узлах 1, 2, 3, 4 соответственно;
A...F — последовательности в соответствующих листьях.

Далее с помощью программы emma было построено множественное выравнивание. У исполнения программы была одна ма-аленькая особенность: были использованы параметры -gapopen и -gapextend со значениями 100.0 и 10.0 соответственно. Эти значения практически запрещают гэпы в выравнивании, а они нам НЕ НУЖНЫ, потому что эволюционная модель НЕ ПРЕДУСМАТРИВАЕТ ни вставок, ни делеций.
Множественное выравнивание использовалось для построений двух матриц: попарных различий (D) и попарных расстояний (вычисленных по формуле Джукса-Кантора). Матрицы были построены с помощью программы distmat пакета EMBOSS. Правда, для первой матрицы был использован пункт меню 0 (расстояние как среднее число несовпадающих нуклеотидов), а для второй — пункт 1 (вычисление расстояний по методу Джукса-Кантора). Матрицы приведены ниже.

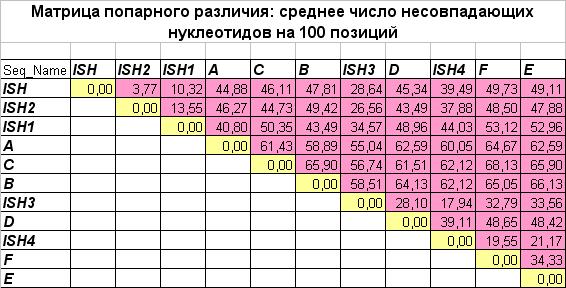
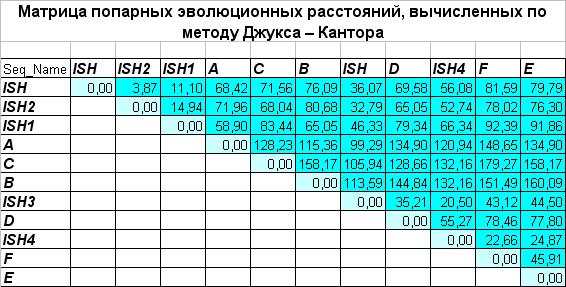
Стоит заметить, что порядок последовательностей в этих двух матрицах немного отличается от такового в исходной матрице. Видимо, это связано с особенностями работы программы distmat...

Следующим шагом стало преобразование всех трёх матриц в таблицы вида "Имя пары" - "Расстояние" и объединение получившихся таблиц в одну. На основе этой общей таблицы (отсортированной по убыванию "истинных" расстояний) был построен график, демонстрирующий зависимость двух оценок расстояния от величины "истинного" расстояния.

На получившемся графике видно, что два способа оценки расстояния, указанных в начале, выдают результаты меньше "истинного" расстояния. Правда, модель Джукса- Кантора лучше считает истинное расстояние, чем обычный подсчёт числа несовпадающих нуклеотидов.
При значениях расстояния, близких к 0, результаты примерно одинаковы (то есть получившиеся оценки расстояний близки к "истинным"). Далее идёт расхождение в сторону уменьшения расстояний. Любопытно, что разница между результатами применения двух способов, названных в начале, выше, чем разница между "истинными" расстояниями и результатами применения модели Джукса-Кантора. Более того, при больших значениях "истинного" расстояния линия, показывающая величину несовпадений (т.е. попарных различий), стремится к горизонтальному положению.