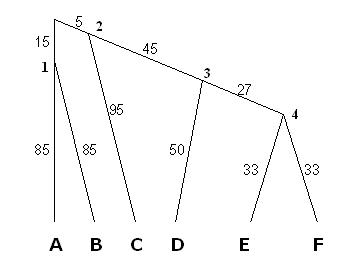
Реконструкция филогенетического дерева с помощью 4-х разных методов

Цель занятия — получить четыре реконструкции филогенетического дерева (рисунок + скобочная формула) и сравнить результат с "истинным" деревом предлагаемой модели.

Сначала целесообразно продемонстрировать то дерево, которое было исходным.

1) Первым этапом нашей работы явилось выравнивание последовательностей, соответствующих листьям дерева (A, ..., F). Последовательности в формате fasta были записаны в один файл (summa.fasta). Программой EMBOSS это воспринимается как выравнивание.

2) С помощью программы ednadist была построена квадратная матрица попарных эволюционных расстояний по методу Джукса-Кантора. Вот она.

SeqName A C B E F D

A 0.0000 1.2823 1.1536 1.3490 1.4865 1.3490

C 1.2823 0.0000 1.5817 1.5817 1.7927 1.2866

B 1.1536 1.5817 0.0000 1.6009 1.5149 1.4484

E 1.3490 1.5817 1.6009 0.0000 0.4591 0.7780

F 1.4865 1.7927 1.5149 0.4591 0.0000 0.7846

D 1.3490 1.2866 1.4484 0.7780 0.7846 0.0000

В этой матрице показаны попарные расстояния между последовательностями A, ..., F. Матрица квадратная, поэтому элемент (i, j) (где i — строка, j — столбец) совпадает по значению с элементом (j, i).

3) Теперь рассмотрим 4 филогенетических дерева, которые были получены с помощью разных программ.

а) Метод UPGMA, программа eneighbor.

             +----------------------------------A         
     +-------3  
  +--4       +----------------------------------B         
  !  !  
  !  +------------------------------------------C         
--5  
  !                              +-------------E         
  !                    +---------1  
  +--------------------2         +-------------F         
                       !  
                       +-----------------------D

Здесь 1-5 — номера узлов (не совпадают с теми номерами, которые были на исходном дереве), A, ..., F — обозначения листьев.
Скобочная формула: (((A:0.57680,B:0.57680):0.13920,C:0.71600):0.02898, ((E:0.22955,F:0.22955):0.16110,D:0.39065):0.35433).

б) Метод Neigbor-Joining (ближайших соседей), программа eneighbor.

  +-------------------------------------------C         
  !  
  !                                    +-----------E         
  !                     +--------------1  
--4---------------------2              +---------------F         
  !                     !  
  !                     +----------------D         
  !  
  !      +---------------------------A         
  +------3                                         
         +----------------------------------------B

Обозначения те же.
Скобочная формула: (C:0.73782,((E:0.19591,F:0.26319):0.25757,D:0.29418): 0.35843,(A:0.47201,B:0.68159):0.11738).

в) Метод Maximum Likelihood (наибольшего правдоподобия), программа ednaml.

                         +----------D         
        +----------------4  
        !                !        +--------F         
  +-----2                +--------3  
  !     !                         +------E         
  !     !  
  !     +------------------------------C         
  !  
--1---------------------------B         
  !  
  +--------------------A

Обозначения те же.
Скобочная формула: (((D:0.34730,(F:0.29295,E:0.23167):0.30071):0.54935, C:1.01137):0.18447,B:0.92458,A:0.70374).

г) Метод Parsimony (максимальной экономии), программа ednapars.

     +-----------B         
     !  
  +--2     +-----D         
  !  !  +--5  
  !  !  !  !  +--F         
  !  +--3  +--4  
--1     !     +--E         
  !     !  
  !     +--------C         
  !  
  +--------------A

Обозначения те же.
Скобочная формула: ((B,((D,(F,E)),C)),A).
Видно, что в формуле отсутствуют значения длин ветвей, поэтому можно сделать вывод, что перед нами кладограмма (а не филограмма).

4) Теперь сравним топологию полученных деревьев. Для этого составим следующую таблицу:

Cравнение топологии исходного филогенетического дерева модели и 4-х вариантов его реконструкции.

Ветвь

ABCDEF

Исходное дерево модели

UPGMA

Parsimony

5) Наконец, опишем результаты сравнения деревьев.

Из таблицы видно, что внутренние ветви всех деревьев совпадают. Это говорит о том, что реконструкция хода эволюции достаточно надёжна, причём всеми методами.

Однако метод UPGMA, как мне представляется, более эффективен (то есть полученное дерево ближе всего к исходному). Почему? Дерево является ультраметрическим, а исходное — почти ультраметрическим (расстояние до 4 из 6 ветвей равно 100, а до двух — 110).

Пожалуй, стоит ещё заметить, что лишь дерево, построенное по методу UPGMA, является укоренённым. Это даёт ещё больше оснований доверять данному методу (для восстановления процесса эволюции). Ультраметрическое же дерево получилось лишь в первом случае (опять-таки метод UPGMA ;).

И в завершение: первые два рассматриваемых метода (UPGMA и Neigbor-Joining) используют матрицу попарных расстояний, а два других — выравнивание последовательностей (т.е. являются символьно-ориентировочными).