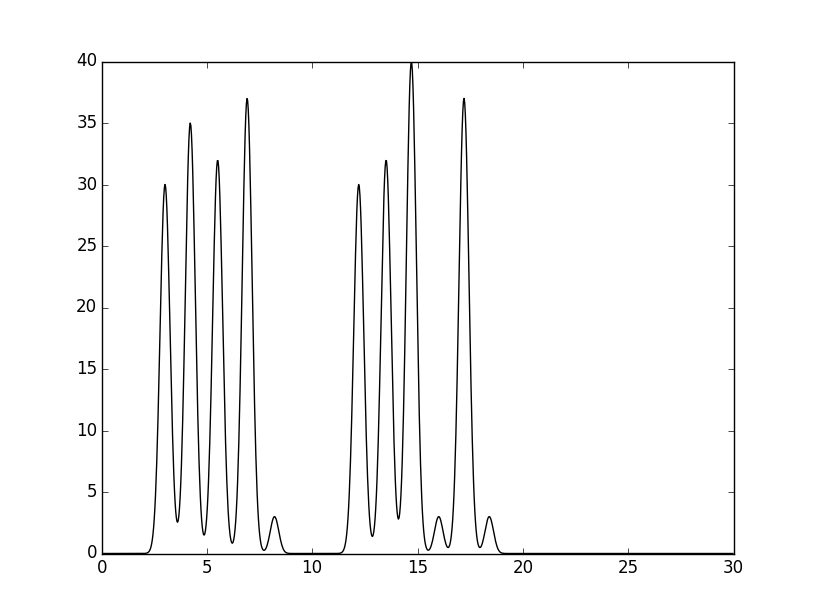
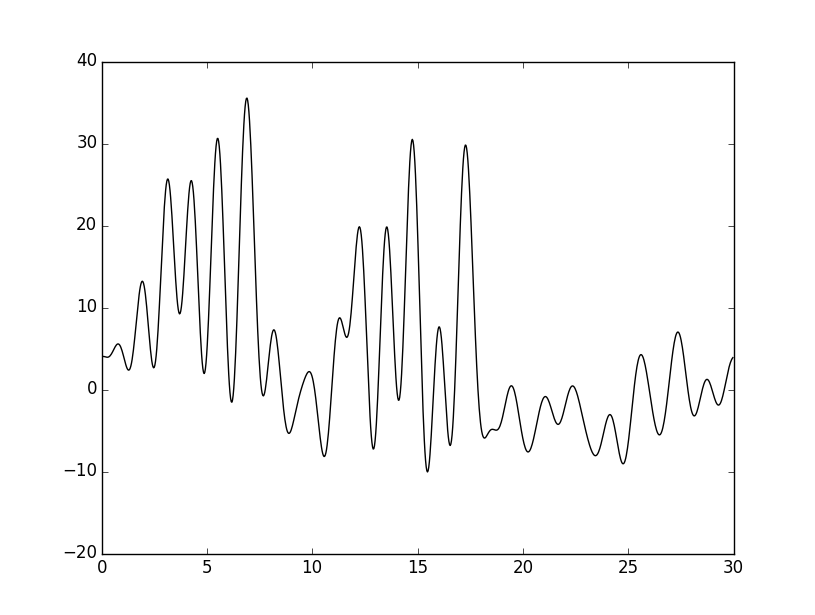
Была выбрана следующая модель для компьютерного эксперимента (на отрезке от 0 до 30 ангстрем): 5 атомов одна молекула (например, B, N, C, O, H) – 6 атомов другая молекула (B, C, F, H, O, H). Поскольку тут идет речь о генерации одномерной картины (Гауссовой функции), а последняя не очень-то реалистична, то моделировать здесь имеет смысл только один аспект – расположение пиков (реалистичность предложенной модели в реальном мире исходя из химических соображений не обсуждалась). В самом начале был создан файл с функцией, описывающей эту модель. На входе программе compile-func.py были поданы следующие параметры (через флаг –g, сумма lambda, beta, gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2)): 30,3,3+35,3,4.2+32,3,5.5+37,3,6.9+3,3.5,8.2+30,3,12.2+32,3,13.5+40,3,14.7+3,3.5,16+37,3,17.2+3,3.5,17.4
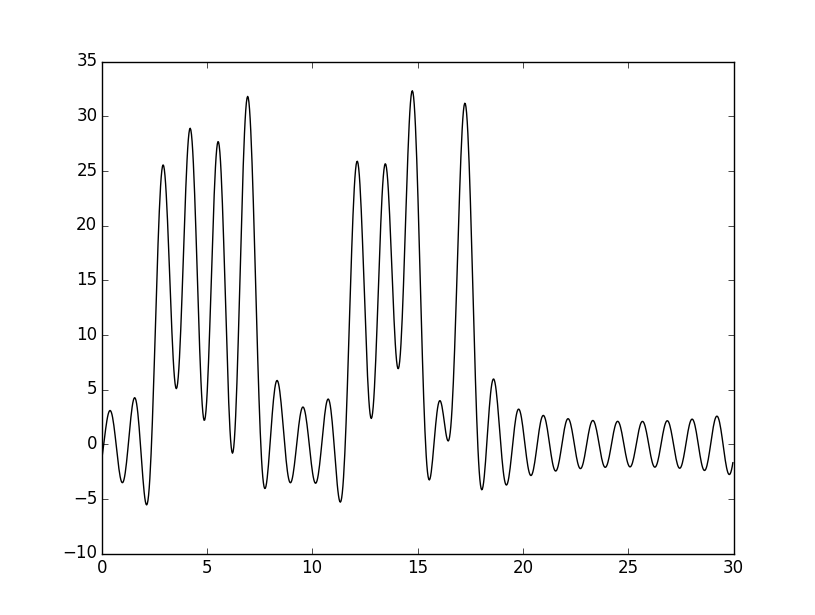
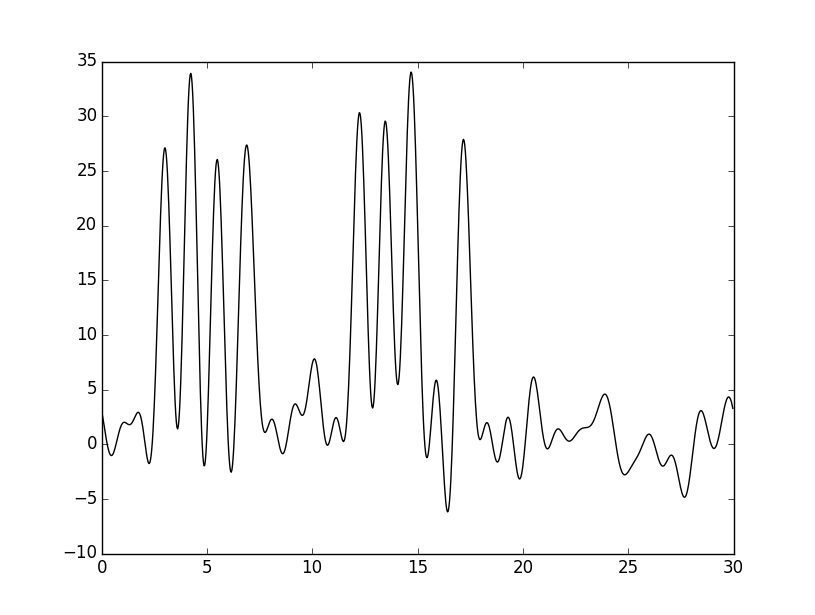
Вот график функции, которую выдал скрипт:

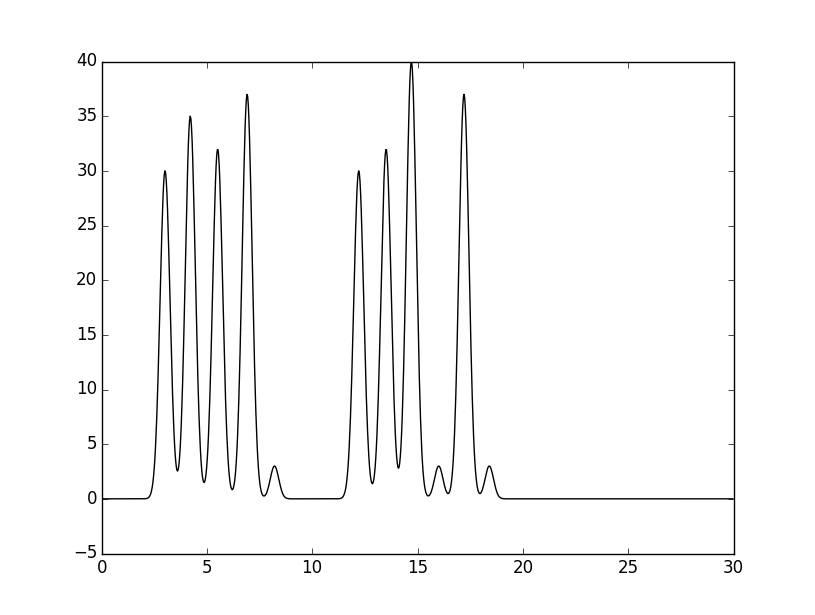
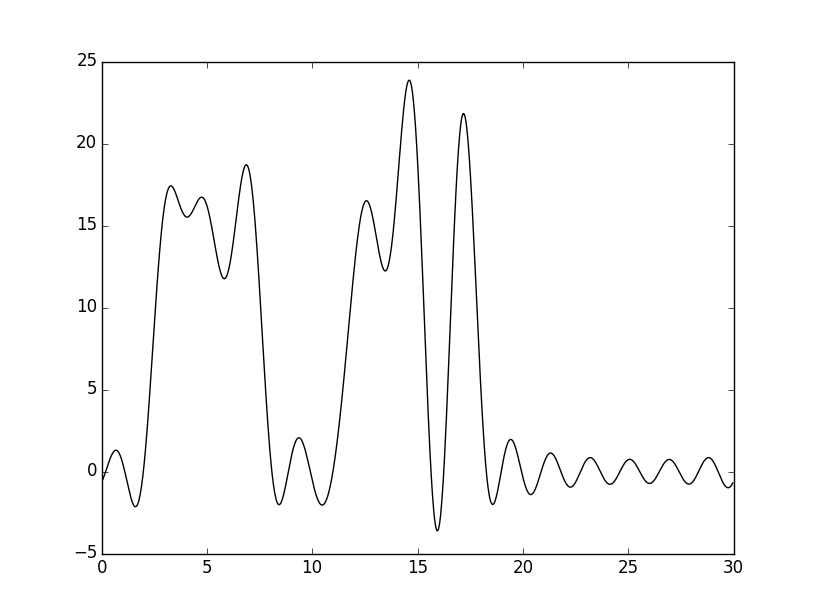
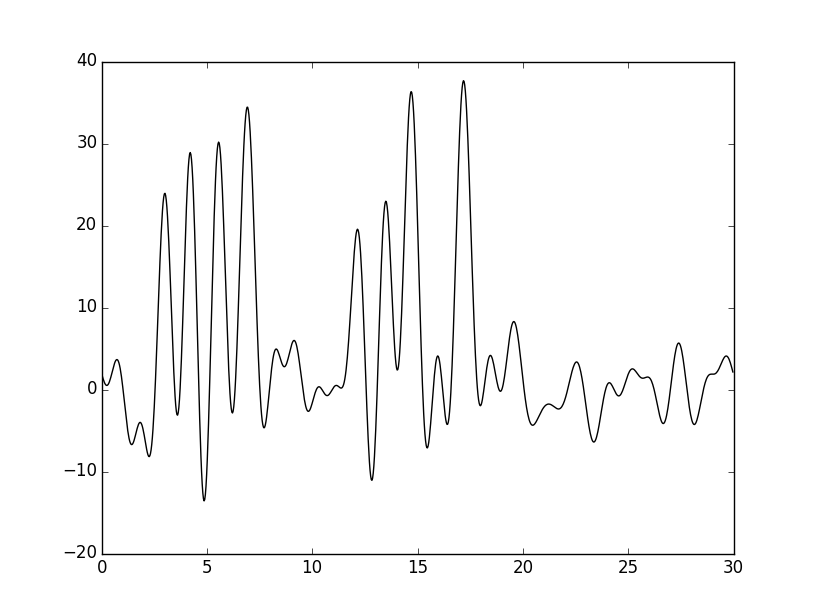
Далее был использован скрипт func2.fourier.py – с его помощью был получен файл с коэффициентами Фурье соответствующей функции (амплитуда и фаза). В нем получилось 498 гармоник. По этому полному набору гармоник была восстановлена функция с помощью скрипта fourier2func.py. Ее график показан ниже. Как и ожидалось, он полностью совпадает с первым графиком, так как использовались все гармоники:
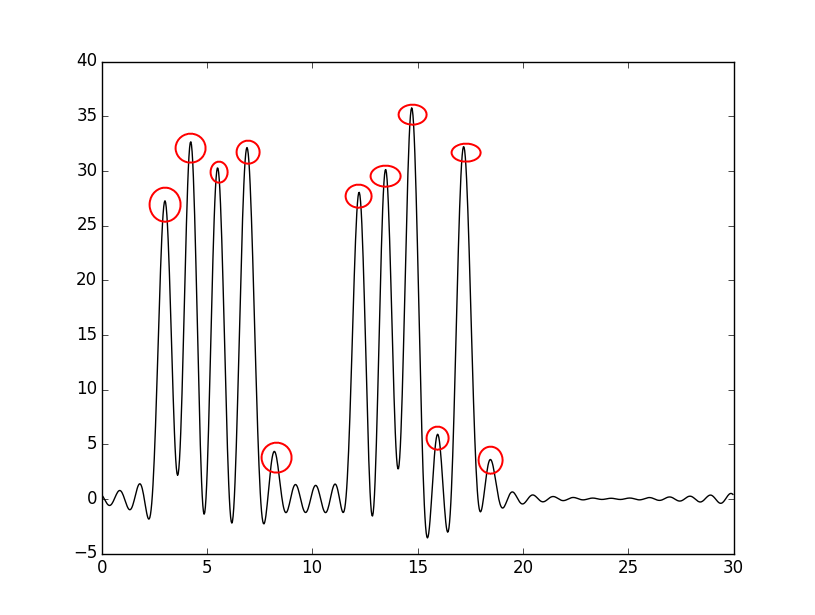
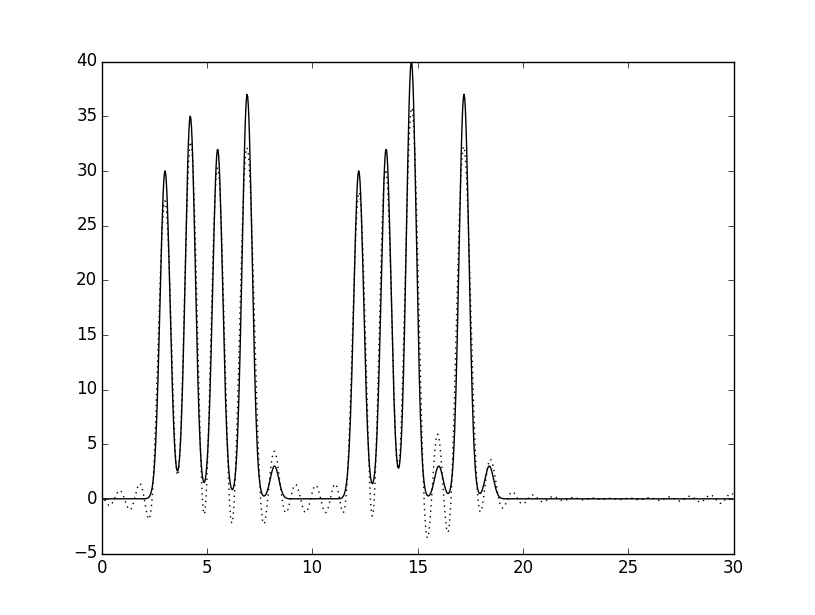
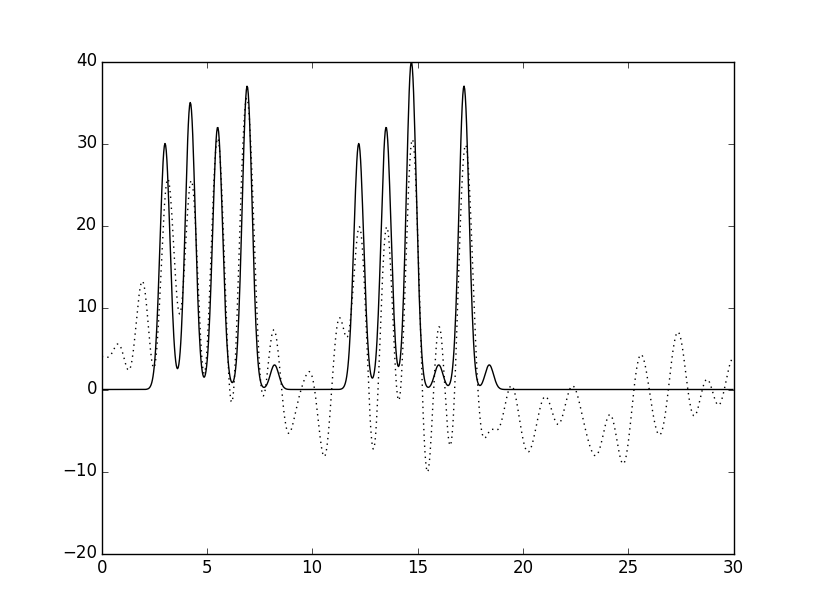
Далее осуществлялся поиск гармоники, с которой восстановление функции происходит отлично (а именно, по графику можно определить положение максимума всех гауссовых слагаемых функции ("атомов")). Отличное восстановление происходит начиная с 30 гармоники. Это можно увидеть на нижних двух графиках (пики на левом графике, которые соответствуют атомам, выделены красным цветом, а справа - черным выделен график исходной функции по всем гармоникам, а точками представлен график, построенный по 30 гармоникам, дабы убедиться, что восстановление действительно отличное!):
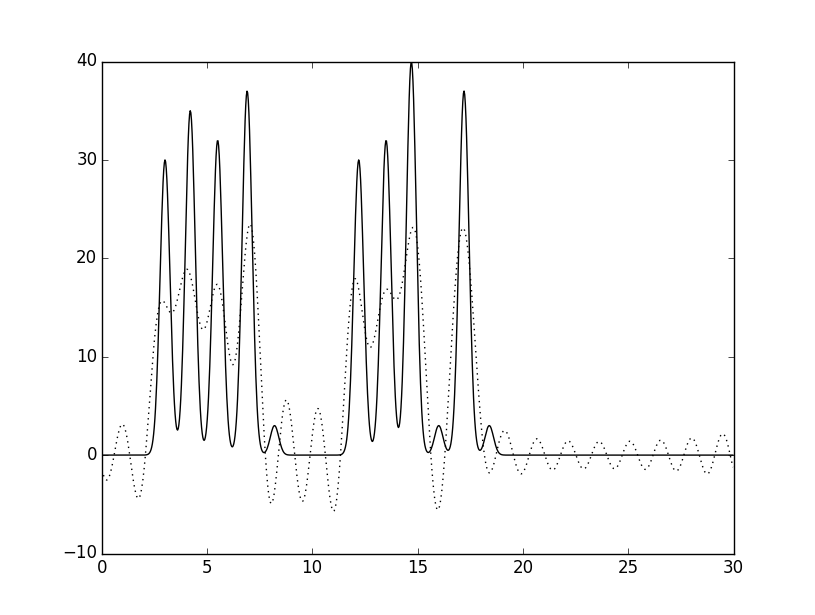
Для примера можно посмотреть на графики, восстановленные по гармоникам 20 (слева – атомы водорода неотличимы – хорошее восстановление, проверено на коллеге) и 15 (это можно назвать средним восстановлением; график справа):
Чтобы вы посмотрели на то, как ложатся эти графики на полноценную функцию по всем гармоникам, привожу следующие рисунки (слева - по 20 гармоникам, справа - по 15):
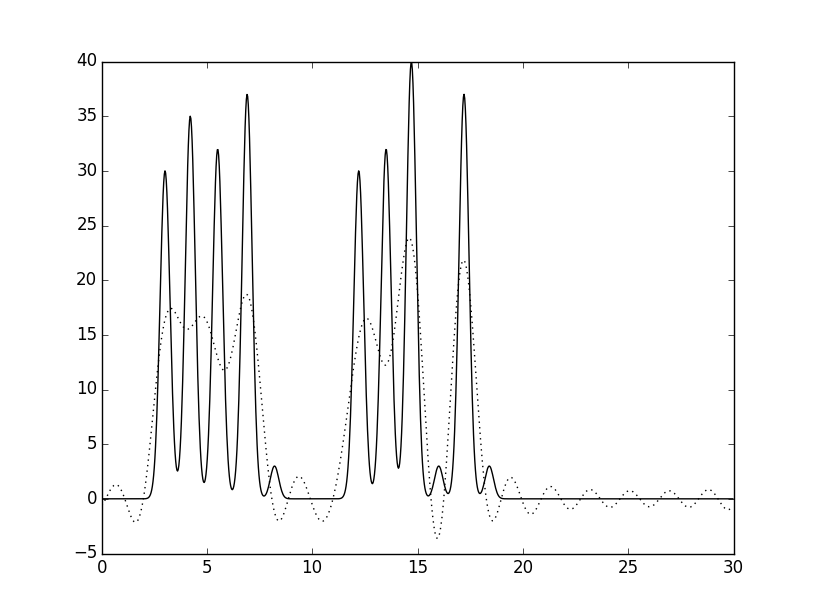
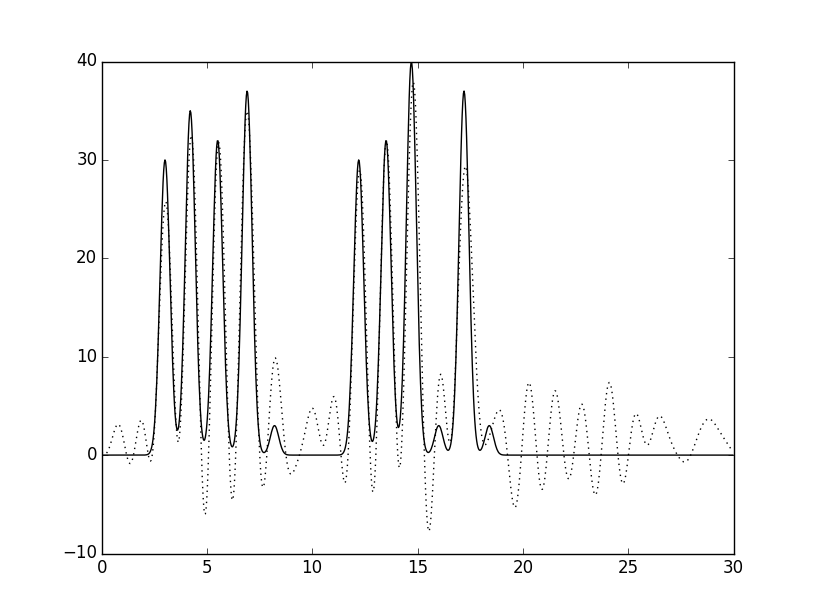
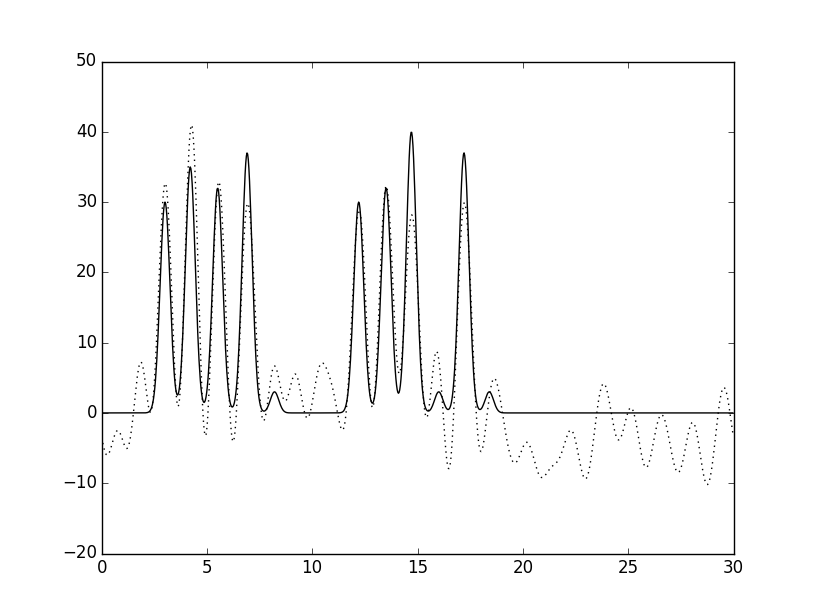
Далее был добавлен шум к амплитудам и фазам при восстановлении по полному набору гармоник 0 – 30. В первом случаем был добавлен шум к амплитудам 20%, а к фазам – 10%. Восстановление из отличного сразу превратилось в среднее-хорошее (смотри рисунок слева). Во втором случае добавленный шум к амплитудам составил 30%, а к фазам – 20%. Тут уже точно восстановление среднее – смотри рисунок справа:
Посмотрим, как это все сходится с полноценной функцией электронной плотности (слева - шум аплитуд 20%, а фаз 10%, справа - шум аплитуд 30%, а фаз 20%):
Если добавить шум к фазам 30%, а к амплитудам - 20%, то получается такая картина:
Если сравнить два графика (слева - шум амплитуд 20%, шум фаз 30%, справа - шум амплитуд 30%, шум фаз 20%), то становится понятно, что фазы вносят больший вклад в восстановление функции электронной плотности, чем амплитуды, так как слева график восстановления выглядит хуже, чем справа.


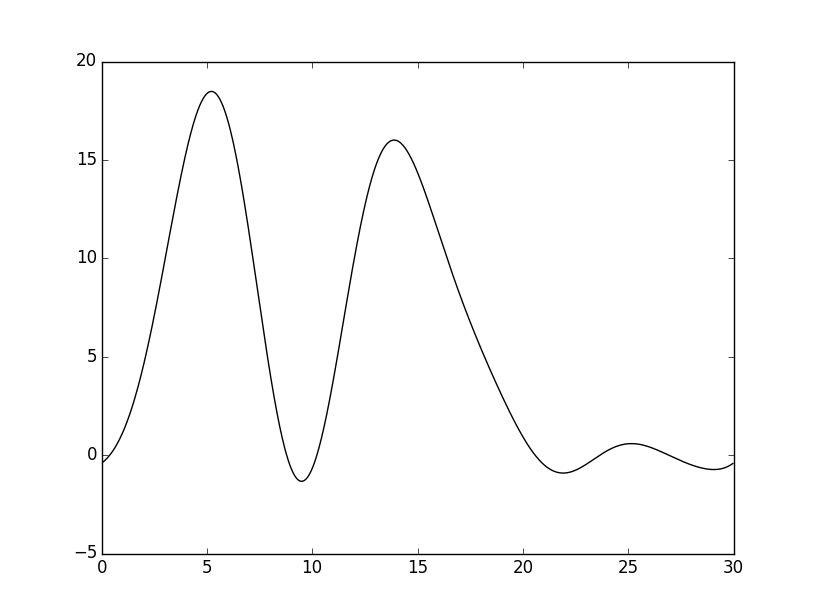
Комментарии ко всем случая приведены в таблице. Для интереса, чтобы видеть, как устроено плохое восстановление – была построена функция для 5 первых гармоник. Полученный график можно увидеть внизу. Видно только два больших горба, говорящие, что у нас 2 молекулы, и позволяющие примерно оценить их форму.
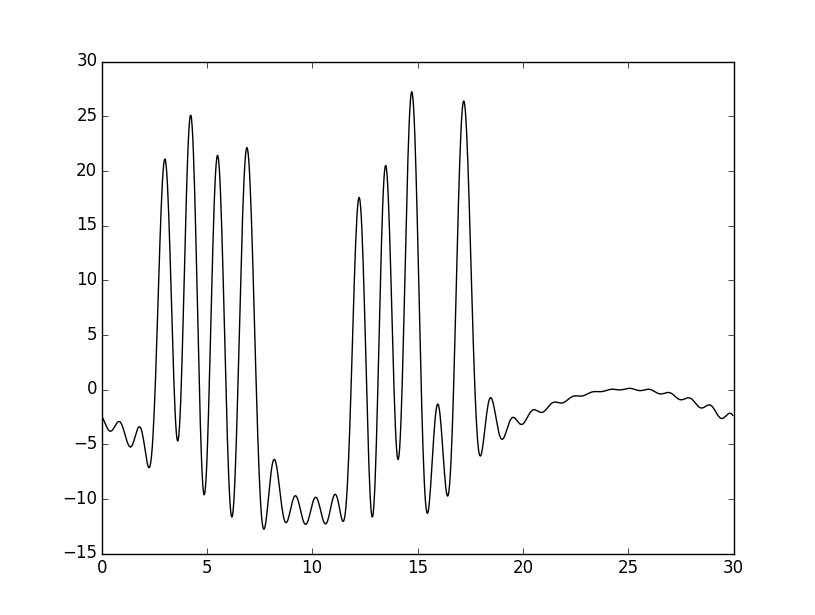
Для начала удалим две начальные гармоники в наборе 0-30, и посмотрим, что из этого получится. На графике внизу видно, как поменялся результат. В принципе, все основные пики различимы, то есть восстановление хорошее, однако точность все равно упала, поскольку видно, как скачет график. Гармоники, обеспечивающие малое разрешение, сохранились, потому структура различима, и это видно, однако на крупных (30 ангстрем), из-за удаления первых двух гармоник наблюдается погрешность.
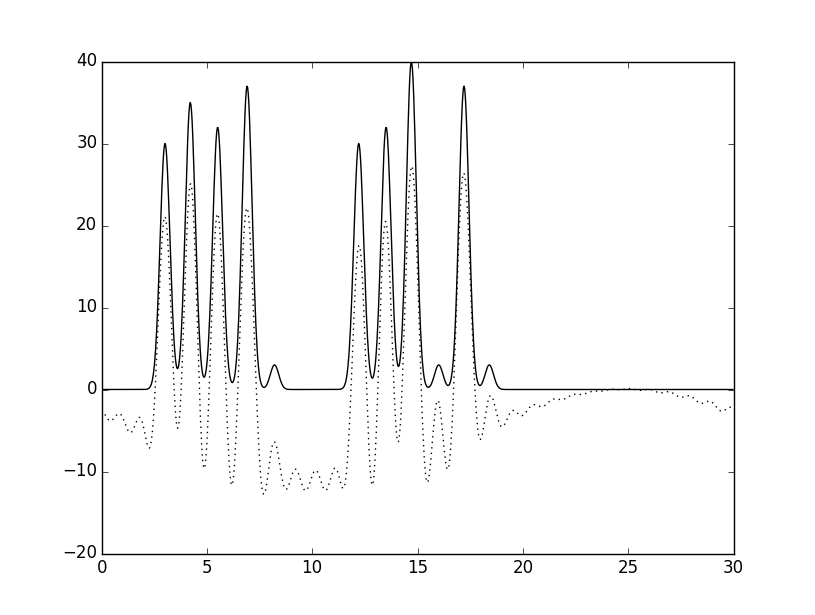
Теперь удалим гармоники с номерами 15, 16 и 17 (из середины набора) и посмотрим, что получится. В этот раз восстановление тоже хорошее (хотя коллега даже оценил как отличное) – это может быть связано с тем, что мы удалили гармоники, отвечающие разрешениям 2-1.75 ангстрем – это не очень большой разброс, тем более следующие гармоники компенсируют этот недостаток данных, иными словами за счет оставшихся гармоник реально восстановить пропущенные.
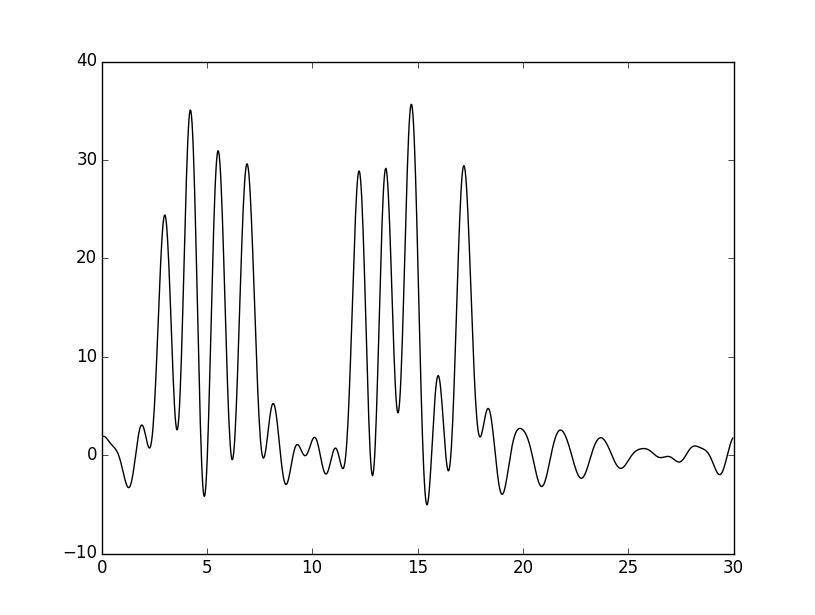
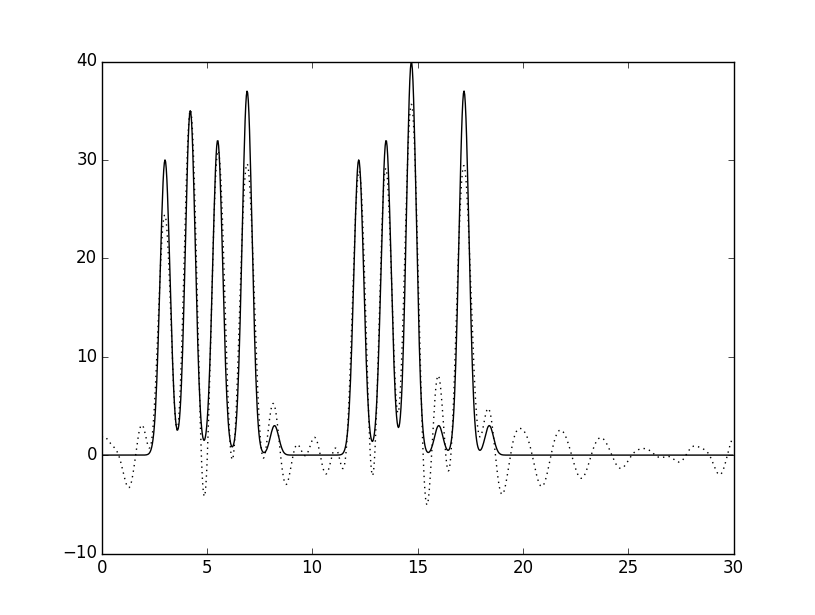
Если восстановить функцию для набора гармоник 0-30, 40, то получится следующий график:
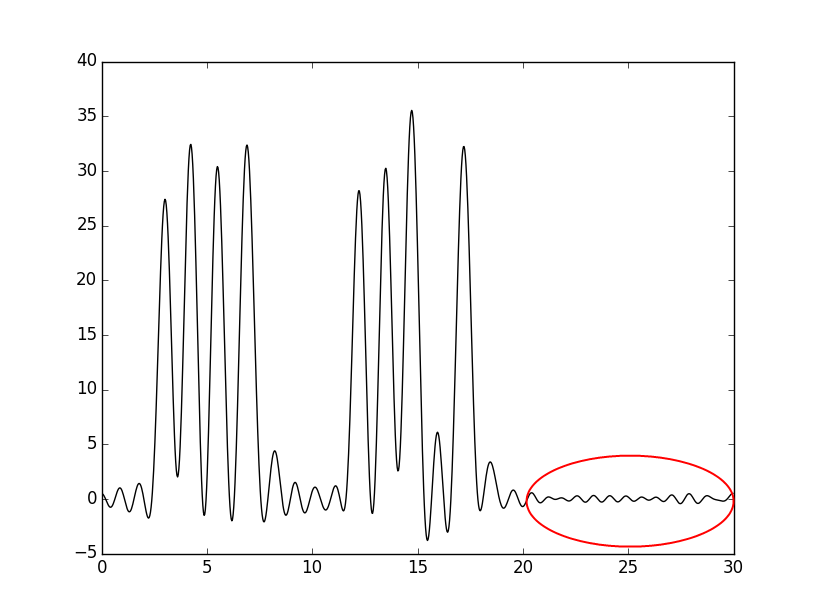
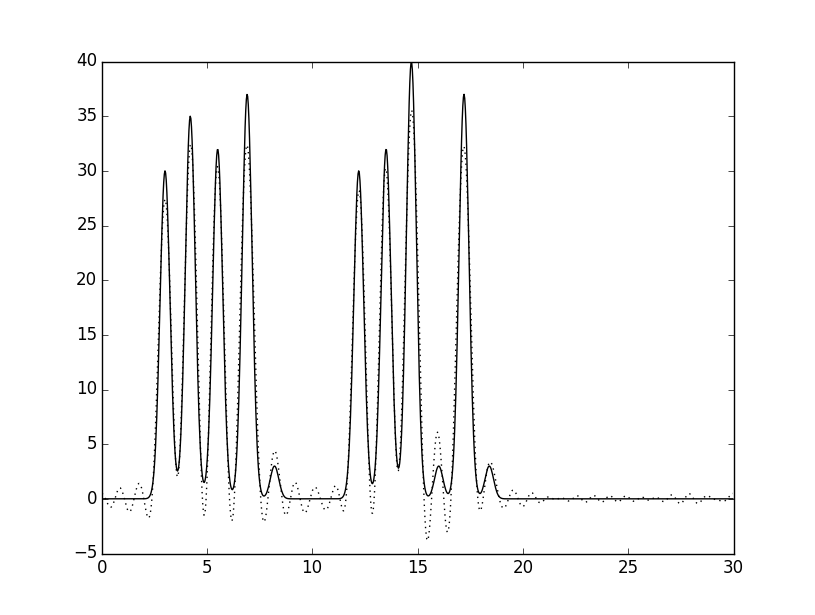
Как видно, он не сильно отличается от того, что для 0-30 гармоник, однако разница есть, и она выделена красным овалом – некие небольшие колебания. Дело тут в том, что мы добавляем дополнительную гармонику, но такую, которая по идее должна давать лучшее разрешение. На самом деле, это жульничество, поскольку нельзя по одной гармонике с таким разрешением детализировать детали соответствующих размеров – для данного примера видно, что в итоговый график привнесены небольшие погрешности.
Если мы хотим определить разрешение структуры по неполному набору гармоник, то, на мой взгляд, надо сделать следующее:
1 - посмотреть на распределение самих гармоник, есть ли сильные разбросы и пятна.
2 - посмотреть на последние номера гармоник, как они распределены.
3 - исходя из общего распределения гармоник и из последних членов прикинуть разрешение структуры. Это очень грубая модель, постараюсь пояснить на примере - для гармоники 0-30,40. Мы видим, что у нас в распределении гармоник есть пробел. Последняя гармоника имеет номер 40, но предпоследняя - 30, а это значит, что вклад в разрешение этой последней гармоникой не будет очень сильным. Поэтому, разрешение определяемой структурой надо оценивать по набору 0-30 с некоторыми погрешностями, вносимыми последней гармоникой.
Вот еще пример. Допустим, у нас отрезок 30 ангстрем. И есть гармоники с номерами 0-5,7-10,15. Разрешение последней (15) гармоники 30/15 = 2 ангстрем. Но какая полнота? Померено всего ячеек для такого набора - 11, а всего 16. Тогда 11/16 = 68.75%. Полнота плохая. Давайте посмотрим на следующую гармонику. У нее номер 10. Разрешение для нее 30/10 = 3 ангстрем. Полнота данных для такого набора - 10/11 = 90.9%. Это значительно лучше, чем для набора с 15 гармоникой в качестве последней. Поэтому будем говорить, что разрешение не 2, а 3 ангстрем. Это элементарный пример, но подобная логика применима во всех, как правило, случаях.