Вычисление параметров для молекулярной механики

Суть задания состоит в определении констант ковалентных взаимодействий для молекулярной механики на основе квантово-химических расчётов.

Нам дана оптимизированная структура этана в виде z-matrix :
```
 $DATA
eth
C1
 C   
 C      1   cc 
 H      2   ch   1   cchv 
 H      2   ch   1   cch   3   d1 0
 H      2   ch   1   cch   3   d2 0
 H      1   ch   2   cch   3   d3 0
 H      1   ch   2   cch   5   d3 0
 H      1   chv  2   cch   4   d3 0

cc=1.52986
ch=1.08439
chv=1.08439
cch=111.200
cchv=111.200
d1=120
d2=-120
d3=180
 $END
```
Вместо значений длин и углов связей стоят переменные.
Наша цель состоит в том, что бы создать порядка 20 разных файлов для расчёта энергии в Gamess с разными значениями по длине одной из связей. Для этого в представленных координатах одна связь или угол отличается названием переменной, но не её значением.
Попробуем автоматизировать процесс с помощью скрипта на bash. Bash это интерпретатор командной строки, который автоматически запускается при присоединении к kodomo.
Составим файл-заготовку для размножения:et.inp.
Для этого к координатам добавьте шапку для dft из предыдущего практикума:
```
 $CONTRL COORD=CART UNITS=ANGS   dfttyp=b3lyp RUNTYP=ENERGY $END
 $BASIS  GBASIS=N31 NGAUSS=6
 POLAR=POPN31 NDFUNC=1 $END
 $GUESS  GUESS=HUCKEL $END
 $system mwords=2 $end
 $DATA 
```
Только изменим информацию о типе входных координат: COORD=CART на COORD=ZMT.
Проверим, работает ли файл-заготовка. Для этого запустим GAMESS. В результате получаем файл et.log без ошибок. Значит, можно перейти к следующему пункту.

Теперь создадим текстовый файл скрипта make_b.bash со следующим содержанием:

#!/bin/bash
### делаем цикл от -10 до 10 ##### 

for i in {-10..10}; do 

#### нам надо рассчитать новую длину связи #####
#### с шагом 0.02 ангстрема,               #####
#### воспользуемся калькулятором bc        #####
#### и результат поместим в переменную nb  #####

     nb=$(echo "scale=5; 1.52986 + $i/50" | bc -l)

#### пролистаем файл et.inp и заменим указание переменной ###
#### на новое значение и пере направим результат в файл   ###

     sed "s/cc=1.52986/cc=$nb/" et.inp  > b_${i}.inp
done

где 1.52986 - стартовая длина изменяемой связи.
Запустим скрипт :

bash ./make_b.bash

В результате получаем 21 inp файл, в каждом - разное значение для переменной сс.

Теперь запустим расчёт для этих файлов. Для этого перед строчкой с
```
done
```
вставим запуск Gamess:
```
gms b_${i}.inp 1 > b_${i}.log
```
Теперь нам надо извлечь значение энергии из log файла. Для этого удобно пользоваться awk.
Сначала в нашем скрипте комментируем запуск Gamess, поставив в начало строчки c gms #. Добавим после закомментированной строчки вызов awk, при этом мы ищем строчку с TOTAL ENERGY и печатаем 4ое поле, считая, что поля разделены пробелами:
```
awk '/TOTAL ENERGY =/{print $4}'  b_${i}.log 
 
```
После запуска скрипта на экране появилось 21 значение энергии.
Теперь удобно было бы выводить и значение длины связи, для этого нам нужно добавить перед вызовом awk распечатку переменой nb. Распечатаем переменную и несколько пробелов без переноса строки:
```
echo -n "$nb    "
```
Теперь запускаем скрипт и далее перенаправляем поток в файл : bash ./make_b.bash > bond .
В результате имеем файл bond с длинами связи и соответствующими значениями энергии.
У нас есть зависимость энергии молекулы от длины одной связи. Нам надо построить эту зависимость в gnuplot.
Запускаем Gnuplot:
```
gnuplot
```
Далее просто введём: plot "bond"
Появился график с точками похожими на параболу. Теперь нам надо найти коэффициенты в функции f(x)=a+k(x-b)^2, которые бы позволили наиболее близко описать наблюдаемую зависимость. Для этого воспользуемся возможностями Gnuplot. Сначала зададим функцию в развернутом виде, в строке gnuplot введём:
```
f(x)=a + k*x*x - 2*k*x*b + k*b*b 
```
И зададим стартовые значения коэффициентов:
```
a=-80
k=1
b=1.5
```
Проведём подгонку коэффициентов под имеющиеся точки в файле bond:
```
fit f(x) "bond" via a,k,b 
```
Значения коэффициентов:
```
a               = -79.7652         +/- 0.0004522    (0.000567%)
k               = 0.563608         +/- 0.02335      (4.142%)
b               = 1.55432          +/- 0.002455     (0.1579%)
```
Далее построим графики функции и значений энергии из Gamess:
```
plot "bond", f(x)
```
Если посмотреть на коэффициенты, то видно, что самый большой разброс имеет K =>функция и точки не полностью совпадают.
Проделаем аналогичные операции для валентного угла HCH, его значения должны изменяться от 109.2 до 113.2. Апроксимация такая же (парабола):
Значения коэффициентов:
```
a               = -79.7647         +/- 1.21e-08     (1.517e-08%)
k               = 3.56076e-05      +/- 6.229e-09    (0.01749%)
b               = 111.38           +/- 9.954e-05    (8.937e-05%)
```
Проделаем аналогичные операции для торсионного угла d3, его значения должны изменяться от -180 до 180 c шагом 12.
Значения коэффициентов:
```
Final set of parameters            Asymptotic Standard Error
=======================            ==========================

a               = 0.00234519       +/- 8.891e-07    (0.03791%)
k               = 3.00014          +/- 0.0002247    (0.007491%)
b               = -79.7623         +/- 6.577e-07    (8.245e-07%)
```
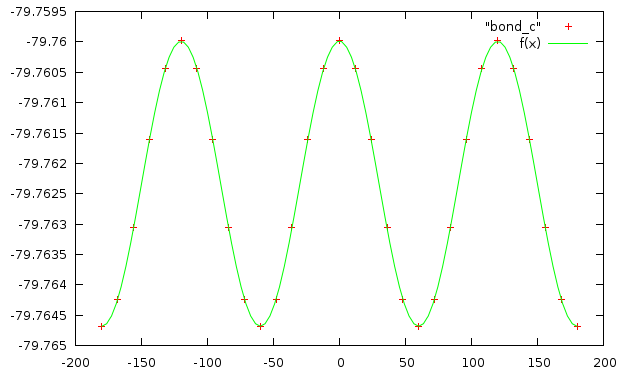
У нас 3 минимума, так как крайние точки совпадают.