Учебный сайт Марины Гладковой

В данном практикуме мне был выдан код доступа к проекту по секвенированию генома Buchnera aphidicola ( SRR4240382).

Buchnera aphidicola относится к гамма-протеобактериям, является первичным эндосимбионтом гороховой тли Acyrthosiphon pisum, питающейся соком растений. По мнению исследователей, предками данного вида могли быть свободноживущие грамм-отрицательные бактерии, близкие к современным энтеробактериям (таким, как E. coli). Анализ последовательностей 16S rRNA подтверждает родство с семейством Enterobacteriaceae. В диаметре достигают 3 мкм, компоненты клеточной стенки во многом схожи с таковыми у энтеробактерий. Однако, в отличие от большинства грам-отрицательных бактерий, у бухнеры нет генов, отвечающих за синтез LPS. Изучение данного вида позволит уточнить эволюционные механизмы и углубить знания о внутриклеточном эндосимбиозе. [1] 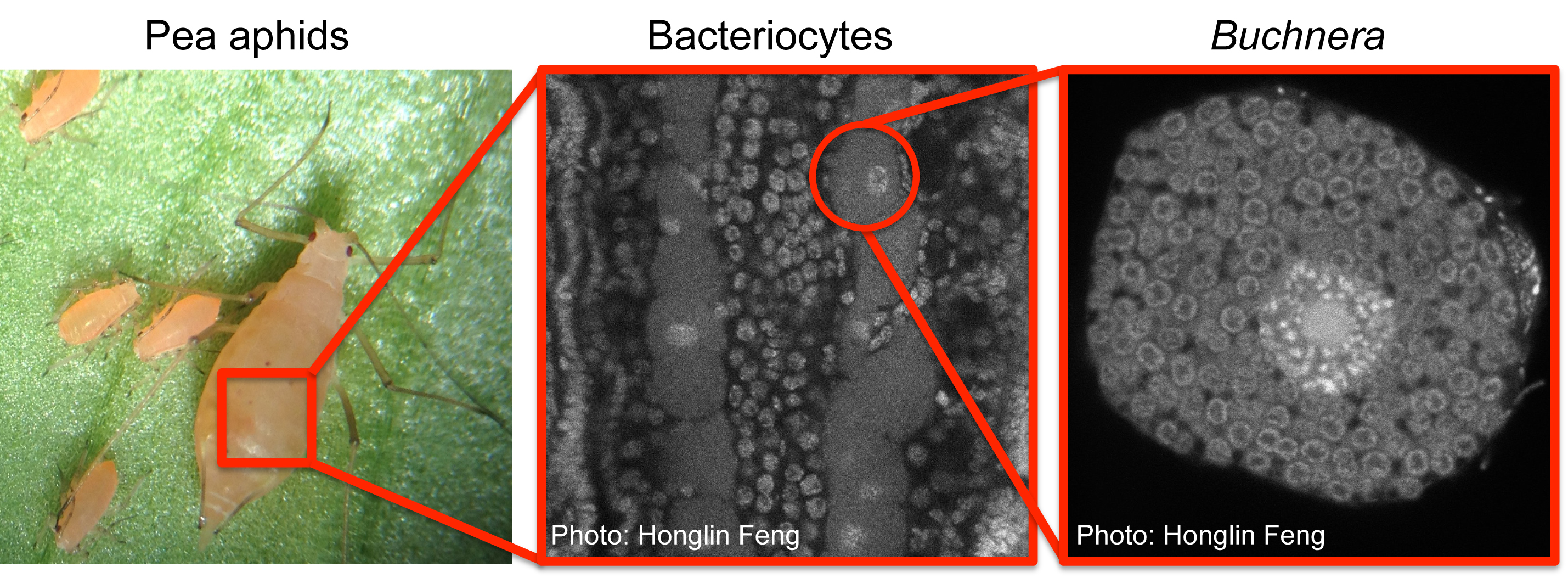Buchnera проживает в специализированных клетках тлей - бактериоцитах, где синтезирует незаменимые аминокислоты для тли-хозяина. Бактериоциты организованы в парный орган - бактериом. [2]

1. Подготовка чтений программой Trimmomatic.

Файл .fastq c чтениями (секвенирование Illumina) был обработан программой Trimmomatic. Таким образом были удалены адаптеры. Сначала был создан файл adapters.fasta с собранием всех известных адаптеров.

Использованная команда	Описание	Результат
java -jar /usr/share/java/ trimmomatic.jar SE -phred33 SRR4240382.fastq SRR4240382_trim.fastq TRAILING:20 MINLEN:30 ILLUMINACLIP:adapters.fasta:2:7:7	Удаление остатков адаптеров, обрезка нуклеотидов с качеством ниже 20 и отбор чтений длины не менее 30 (где 2 - отдельные несовпадения, 7 - порог для палиндромной шпильки, 7 - порог для простой шпильки)	SRR4240382_trim.fastq

Выдача программы:

Input Reads: 17756177 Surviving: 11919768 (67,13%) Dropped: 5836409 (32,87%)

Размер файла уменьшился с 1808 Мб до 1173 Мб, что говорит о достаточно хорошем результате чистки. Однако, скорость работы программы не самая быстрая.

2. Подготовка k-меров.

Подготовка k-меров была произведена в программе velveth. Она предназначена для создания набора данных для последующей обработки программой velvetg. Velveth принимает на вход несколько последовательностей, строит хэш-таблицу, в результате получаются файлы Sequences и Roadmaps (также Log с отчетом о работе) в отдельной директории. Длина k-мера (хэша) соответствует длине хэшируемого слова в п.о. В задании она была указана: k=29. Выбор данного параметра зависит от технической задачи:

• k нечетно для избежания палиндромов
• k<=31 по дефолту (31 - max хэш-длина по умолчанию, может быть изменена)
• k меньше длины ридов (иначе отсутствуют перекрывания)

Чем больше значение k, тем меньше ложных перекрываний ридов, но вместе с тем меньше общее покрытие. При запуске надо указывать длину k-мера и тип чтений (короткие или длинные, парные или непарные...). Возможные форматы входных файлов: .fasta (default), .fastq, .fasta.gz, .fastq.gz, .sam, .bam, .eland, .gerald. [3] Чтения в нашем случае короткие и не парные (short). Выходные файлы записаны в папку velveth.

Команда запуска:

velveth velveth 29 -short -fastq SRR4240382_trim.fastq

3. Сборка на основе k-меров.

Cборка на основе k-меров с помощью программы velvetg на вход получила данные из предыдущего этапа. Velvetg строит граф де Брёйна - ориентированный n-мерный граф из m символов, отражает пересечения между последовательностями символов. Он имеет mⁿ вершин, состоящих из всех возможных последовательностей длины n из данных символов (т.е. k-меры являются вершинами), ориентированные рёбра соединяют так называемые префикс- и суффикс-последовательности. Один и тот же символ может несколько раз встречаться в последовательности. [4] При запуске программы с параметрами по умолчанию можно получить файл .fasta с контигами и статистические данные в указанной директории.

Команда запуска:

velvetg velveth

Результаты работы velvetg:

• изначально 2430680 "пре"-вершин, в итоге — 3266 (количество вершин не обязательно соответствует количеству контигов, так как мы ограничили снизу контиги длиной 29, "нормальные" контиги описаны в файле contigs.fa);
• N₅₀ = 13439;
• max длина контига — 67459;
• файлы с графами: PreGraph, LastGraph, Graph;
• файл с информацией о вершинах графа - stats.txt:
  1) длина вершины в k-мерах (для расчёта длины в нуклеотидах добавляем k–1);
  2) in — число входящих рёбер с 5'-конца;
  3) out — число выходящих рёбер с 3'-конца;
  4) колонки *_cov и *_Ocov содержат информацию о покрытии с разницей в методе подсчета (*_Ocov — более строгий)
• файл с контигами в формате .fasta — contigs.fa (последовательности длины не менее 2k, можно установать специально ограничение на минимальную длину контига, чего мы не делали);
• встречаются контиги с аномально большими покрытиями (как, например, контиг с ID 3234 и покрытием 43986, однако его длина составляет 1 k-мер, чем и объясняется такое большое отклонение покрытия);
• достаточно сложно судитьо контигах с аномально маленьким покрытием, так как их слишком много (только контигов с покрытием меньше 5 несколько сотен)

4. Анализ.

Для анализа были взяты три самых длинных контига (ID 1, ID 13, ID 8). Каждый из них был обработан по алгоритму blastn megablast в паре с хромосомой Buchnera aphidicola (GenBank AC: CP009253).

ID	Координаты в геноме	Max score (bits)	Total score	Query cover	E-value	Identities	Gaps
1	532032-550219	12576	26469	64%	0.0	14656/18457 (79%)	488/18457 (2%)
8	295935-303252	3947	13037	67%	0.0	5696/7429 (77%)	186/7429 (2%)
13	37007-44693	6909	19815	72%	0.0	6424/7741 (83%)	97/7741 (1%)

* В таблице приведены только участки выравниваний с максимальным Score.

Построенные для 3 максимальных по длине контигов выравнивания оказались вполне приемлемыми. Аналогичный анализ для двух контигов с аномально большим покрытием выполнить не удалось, так как длина исследуемых последовательностей оказалась абсурдно маленькой, для построения выравнивания (можно попробовать изменить Expect thershold, но мне это не помогло). По данным FAQ программы, возможной причиной ошибки может также являться фильтрация участков малой сложности. Поиск без фильтрации, тоже не дал результатов.