Для оценки качества восстановления функции ЭП была выбрана следующая модель:
Рис.1. Модель взаимодействия двух молекул:

Данная модель отвечает следующим условиям:
- на отрезке [0,30] (ангстремы) расположены две молекулы;
- атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга;
- всего 5-7 атомов (2+3 или 2+3+2; возможны другие варианты).
Функция ЭП имеет вид нескольких гауссовых кривых с центром в разных точках. Гауссова функция, генерируемая скриптом compile_func.py, определяется числами lambda, beta, gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2), где lambda - высота колокола(пропорциональна числу электронов),beta - ширина колокола(пропорциональна диаметру атома), gamma - положение максимума.
Для выбранной модели были приближенно подобраны следующие параметры:
>>> python compile_func.py -g 2.5,3,3+10,3,4.3+2.5,3,5.6+2.5,3,7.7+15,3,8.7+17.5,3,9.8
Результат работы скрипта - файл func.txt c функцией на интервале [0,30] (30 следует понимать как 30Å) и смоделированный 1D график электронной плотности молекул, отображающий заданную вручную функцию ЭП модели HBeH--HCN.
Рис.2. График электронной плотности

С помощью скрипта func2fourier.py был получен файл calc_fourier.txt с коэффициентами Фурье, в котором для каждой гармоники записаны ее номер, амплитуда и фаза.
>>> python func2fourier.py -i func.txt -o calc_fourier.txt
По полному набору гармоник (всего - 499) с помощью скрипта fourier2func.py была восстановлена изначальная функция. Полученный график полностью совпадает с исходной функцией(рис.3А).
Далее, для определения минимального необходимого набора гармоник n_0 использовался скрипт fourier-filter.py. Были использованы следующие параметры n: 0-5, 0-15, 0-25, 0-30.
Пример команд для гармоник 0-5:
>>> python fourier-filter.py -i calc_fourier.txt -o func_restrained_0_5.txt -r 0-5
>>> python fourier2func.py -i func_restrained_0_5.txt -o func_restored_0_5.txt
>>> python fourier2func.py -i func_restrained_0_5.txt -o func_restored_0_5.txt
Рис.3. Восстановленные по различным наборам гармоник графики электронной плотности
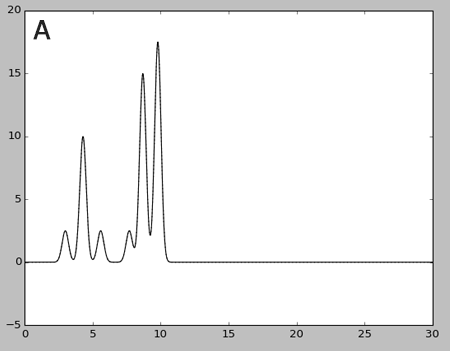




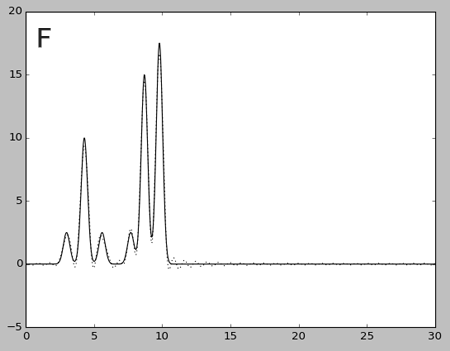
Графики восстановленных по разным наборам гармоник функций (пунктир), наложенные на график исходной функции.
A: все гармоники; B: 0-5; C: 0-15; D: 0-25; E: 0-30; F: 0-35.
A: все гармоники; B: 0-5; C: 0-15; D: 0-25; E: 0-30; F: 0-35.
График функции, восстановленной по гармоникам 0-5(Рис.3B) дает представление о расположении молекул. Отдельные атомы различить нельзя.
Восстановление функции по гармоникам 0-15(Рис.3C) все еще не позволяет различить отдельные атомы во второй молекуле и выделить атомы водорода.
Восстановление функции по гармоникам 0-25(Рис.3D) и 0-30(Рис.3E) уже дает расщепление пика второй молекулы на C и N, однако точно отделить атомы водорода от фона едва ли выйдет.
Восстановление функции по гармоникам 0-35(Рис.3F) позволяет, наконец-то, различить все атомы в молекулах модели, и, более того, лучше разграничивает отдельные пики, чем исходная функция. Следовательно, считаем, что это n_0.
Итак, для приближения моделирования к эксперименту число используемых гармоник уменьшено до 35.
Для большей достоверности рассматриваемой модели добавим шум к ее характеристикам. Для добавления шума к амплитудам и/или фазам и получения расчетов и графиков использовались следующие команды:
>>> python func2fourier.py -i func.txt -o calc_f10.txt -F 10
>>> python fourier-filter.py -i calc_f10.txt -o func_restrained_f10_0_35.txt -r 0-35
>>> python fourier2func.py -i func_restrained_f10_0_35.txt -o func_restored_f10_0_35.txt
список всех команд
>>> python fourier-filter.py -i calc_f10.txt -o func_restrained_f10_0_35.txt -r 0-35
>>> python fourier2func.py -i func_restrained_f10_0_35.txt -o func_restored_f10_0_35.txt
список всех команд
Расчеты были выполнены для F=10, F=50, P=10, P=50, F=10|P=10, F=30|P=30. Добавление шума приводит к тому, что к каждой амплитуде прибавляется случайное число, распределенное нормально с параметрами: среднее = 0, среднее квадратичное отклонение (сигма)=0.2*F. Аналогично действует параметр -P <число>
Рис.4. Восстановление функции распределения ЭП с разными уровнями шума
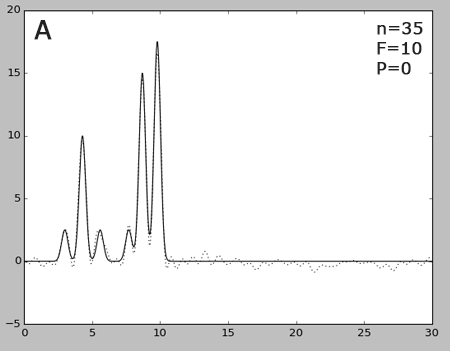



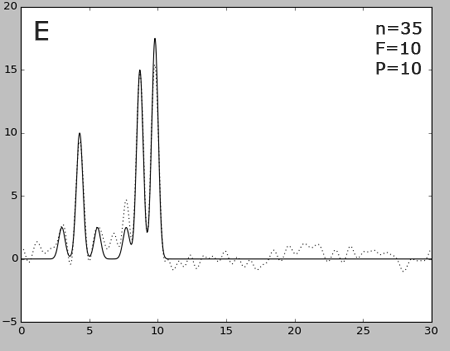

Графики восстановленных функций с разными уровнями шума (пунктир), наложенные на график исходной функции.
При добавлении 10% шума к амплитуде (рис.4A) и к фазе (рис.4С) все еще можно различить атомы водорода, хотя по сравнению влияния шума на эти величины видно, что вклад фазы больше, чум вклад амплитуды. Однако ни при 50% уровне шума амплитуды (рис.4B), ни при 50% шуме фазы (рис.4D) выделить атомы водорода уже не удается (во втором случае фоновые колебания обладают большей амплитудой). Различить атомы Be, C и N можно. То же самое касается и параллельного добавления шума к обеим величинам: при 10% шуме (рис.4E) уже нельзя определить атомы водорода - сравнительно большой амплитудой обладают фоновые колебания. При 30% шуме (рис.4F) атомы крупнее водорода все еще можно отличить от фона.
Итак, в эксперименте все коэффициенты ряда Фурье получаются с ошибкой. Кроме того, не все до последнего номера n удается измерить. Для имитации подобной ситуации будем восстанавливать функцию распределения ЭП из неполного набора гармоник (n исходное = 35).
Рис.5. Восстановление функции распределения ЭП по неполным наборам гармоник

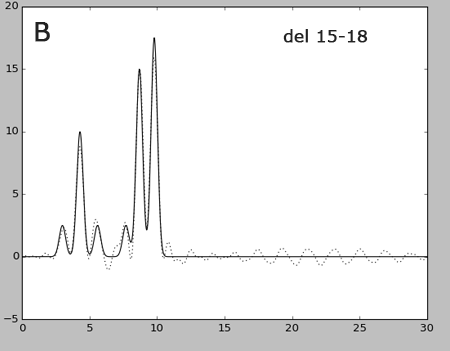

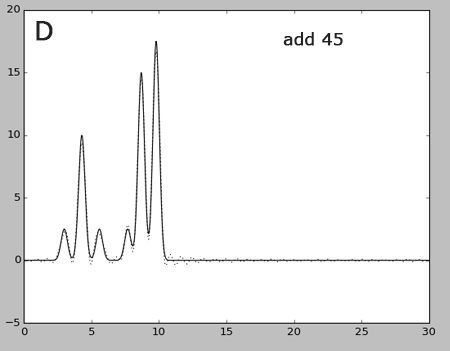
Графики восстановленных функций с разными уровнями шума (пунктир), наложенные на график исходной функции.
Отсутствие гормоник в начале (рис.5А) и в середине (рис.5B-C) неоднозначно сказывается на восстановлении функции ЭП: в первом случае меняется общий вид графика функции (появляется заметная косинусоида). Если при удалении гармоник в начале атомы водорода еще можно различить, то при удалении первого набора из середины (рис.5B) они уже определя.тся с трудом, а при удалении большего количества гармоник (рис.5C) это становится невозможным. Что касается добавления 45 гармоники, то изменения практически отсутствуют: появляется шумовое "волнение" на линейных участках кривой. Все вышесказанное согласуется с тем фактом, что при увеличении n вклад гармоники в значение функции уменьшается.
Теперь смоделируем более-менее приближенную к реальности ситуацию: к неполному набору гармоник добавим 15% шум и к амплитудам, и к фазам.
Рис.6. Восстановление функции распределения ЭП по неполному набору гармоник с 15% шумом F и P


Графики восстановленных функций с разными уровнями шума (пунктир), наложенные на график исходной функции.
На рисунке выше видно, что расположение молекул и крупных атомов достаточно хорошо сохраняются, однако положение водорода установить не удастся.
Разрешение для полного набора гармоник соответствует длине волны гармоники с наибольшим номером:
d0=T/n
где T=30, d0 - разрешение полного набора гармоник.
Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо сообщить полноту данных — процент гармоник с длиной волны не меньшей d от максимально возможного, присутствующих в наборе. Поэтому, учитывая нехватку гармоник, разрешение можно рассчитывать следующим образом:
d=d0/k
где k - полнота данных в долях единицы, d0 - разрешение полного набора гармоник.
На качество восстановления функции ЭП наиболее сильно влияют следующие факторы: шум фаз и неизмеренные гармоники из середины.
Таблица.1. Восстановление функции по коэффициентам ряда Фурье

Таблица в формате .docx.