Фурье

Семестры:

Восстановление структуры по "экспериментальным данным PCA" в одномерной модели

Создание модельной функции электронной плотности в одномерной элементарной ячейке

Первым делом предстояло для компьютерной модели из двух молекул получить 1D график электронной плотности с помощью гауссовой функции:

gauss = λ*exp(-(β^2)*(X-γ)^2)

В качестве модели на отрезке [0, 30 Å] я расположила молекулу А, состоящую из двух атомов, и молекулу B, состоящую из трех атомов, так чтобы между ними было расстояние 4 Å. Реализовать модель помогла программа compile-func.py, которая была запущена с параметрами:

compile-func.py -g 35,3.5,11+10,3,12.2+20,3.1,16.2+40,3.4,17.7+25,3,19

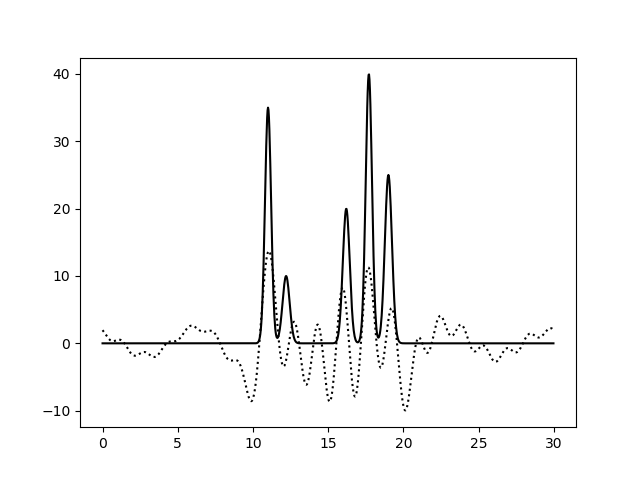
Тройка чисел под параметром -g соответствует параметрам λ, β, γ в выше приведенной формуле, а число таких троек соответствует числу атомов в модели. При этом λ - высота пика (отражает число электронов в атоме), β - ширина, а γ - координата максимума пика. В результате я получила файл func.txt и следующее изображение функции электронной плотности.

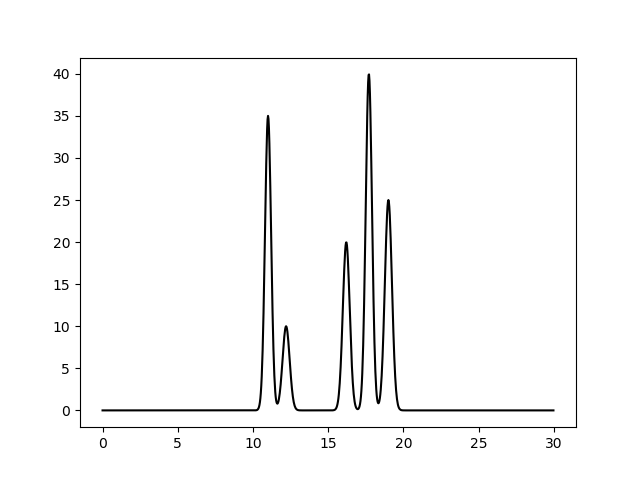
Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные

С помощью скрипта func2fourier.py был получен файл func_ft.txt, в котором для каждой гармоники восстановлены амплитуда (F) и фаза (phi).

func2fourier.py -i func.txt

Всего в этом файле оказалось 499 гармоник. Однако в реальном эксперименте невозможно рассчитать параметры для всех сигналов, поэтому далее предстояло определить минимальное число гармонических слагаемых (N), необходимых для отличного качества восстановления функции электронной плотности (таблица 1).

Восстановление функции электронной плотности по модельным данным

Далее я запустила программу fourier2func.py

fourier2func.py -f func.txt -i func_ft_filtered.txt

Здесь func_ft_filtered.txt - файл, полученный из func_ft.txt, с набором параметров для гармоник под номерами 0..n. Варируя переменную n, были получены следующие изображения.

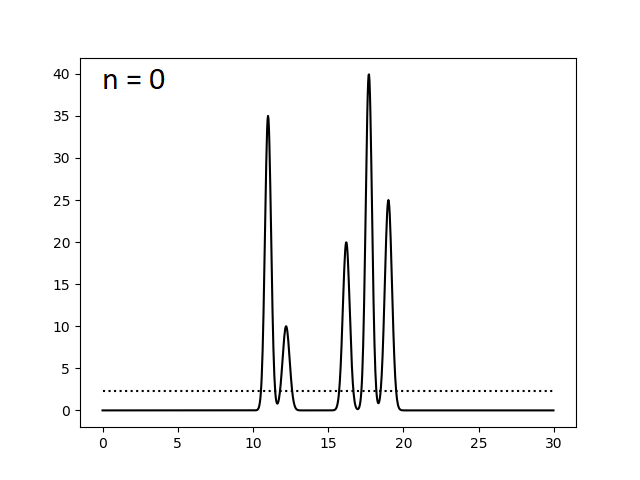
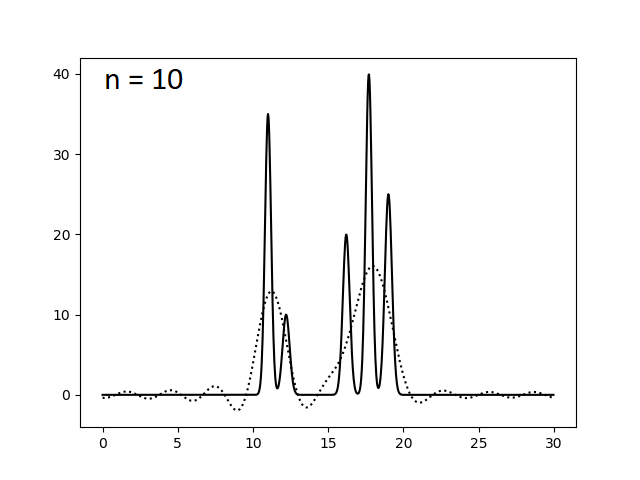
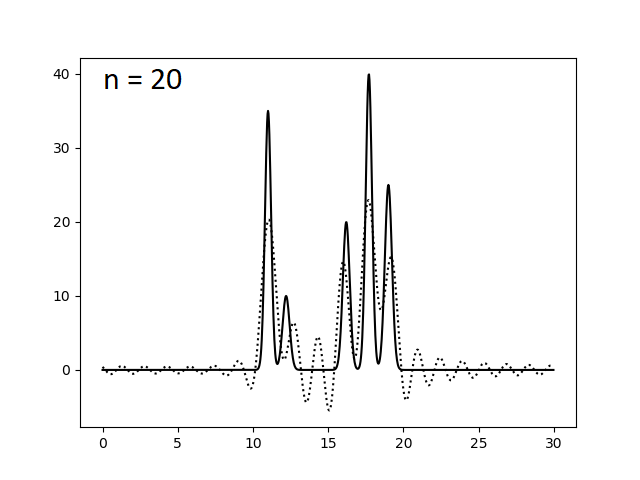
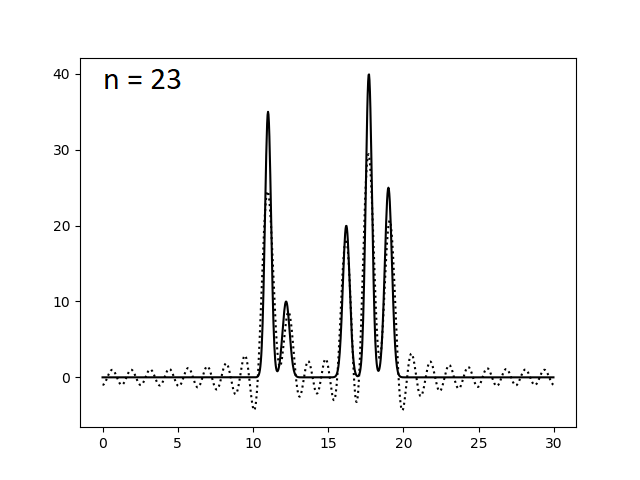
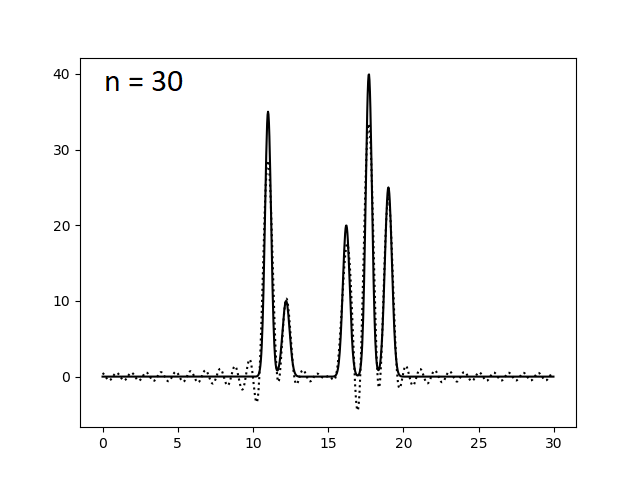
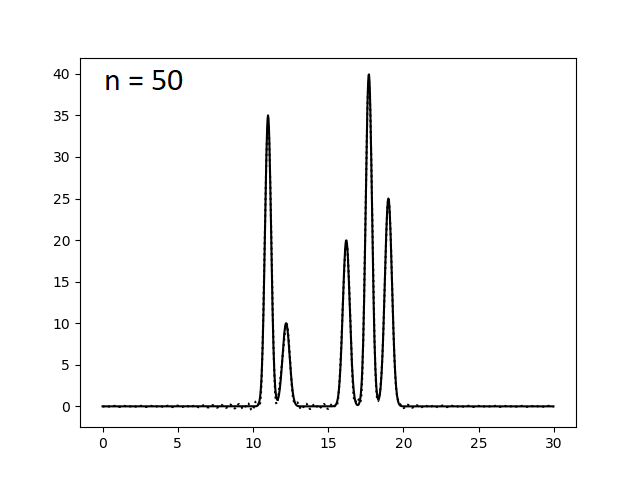
Оказалось, что для отличного восстановления функции электронной плотности нашей модели достаточно N = 23 гармоник. Однако это справедливо лишь для утопической модели идеального эксперимента, где отсутствуют ошибки в измерении интенсивности сигналов (амплитуд) и фаз. Поэтому теперь искусственно введем в наши данные погрешности при расчете коэффициентов ряда Фурье. Этого можно добиться, указав при запуске скрипта func2fourier.py параметры -F (% шума для амплитуд) и -P (% шума для фаз). Ниже приведены изображения, полученные при восстановлении функции электронной плотности по полному набору гармоник (N = 23) по зашумленным данным.

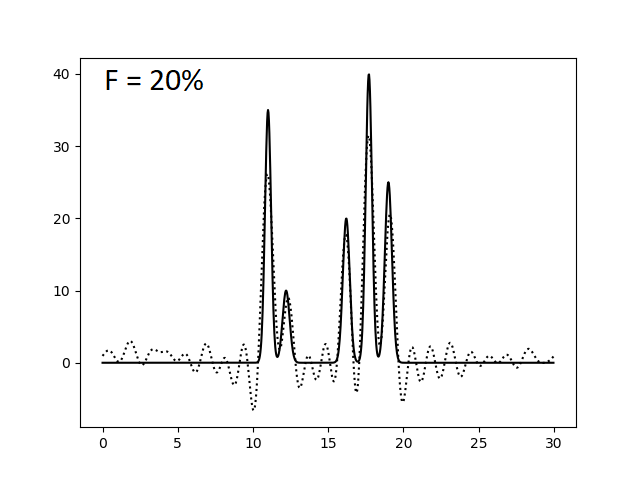
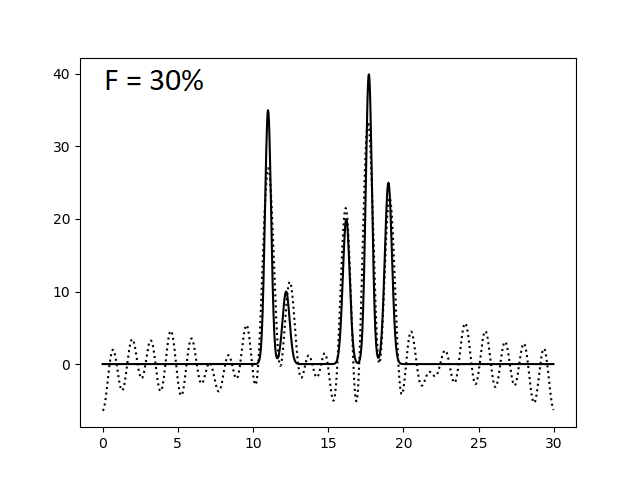
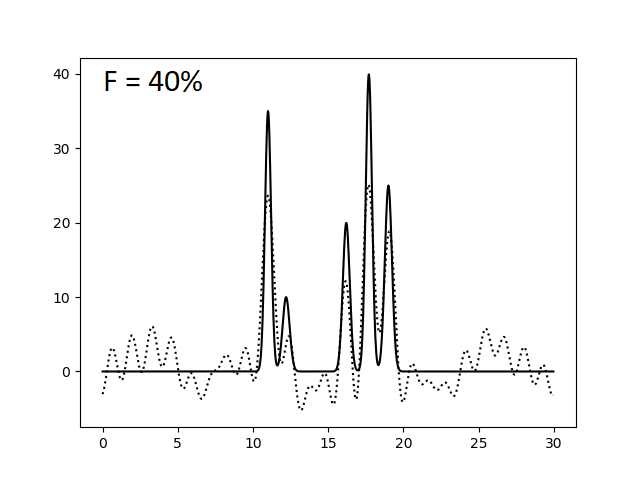
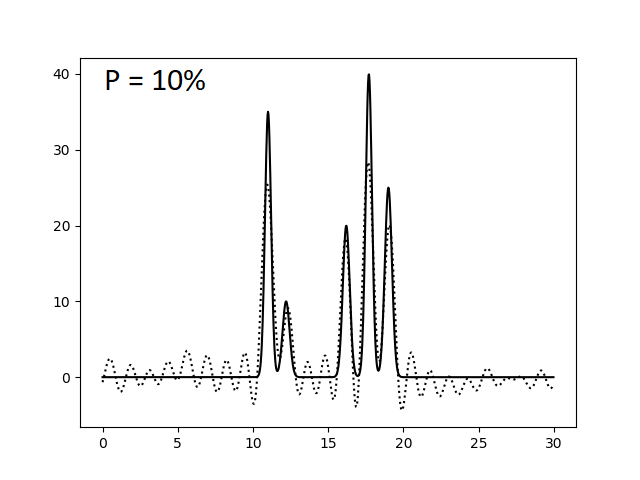
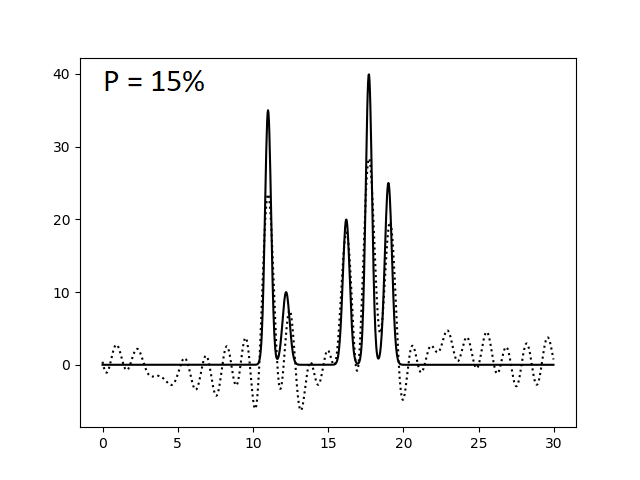
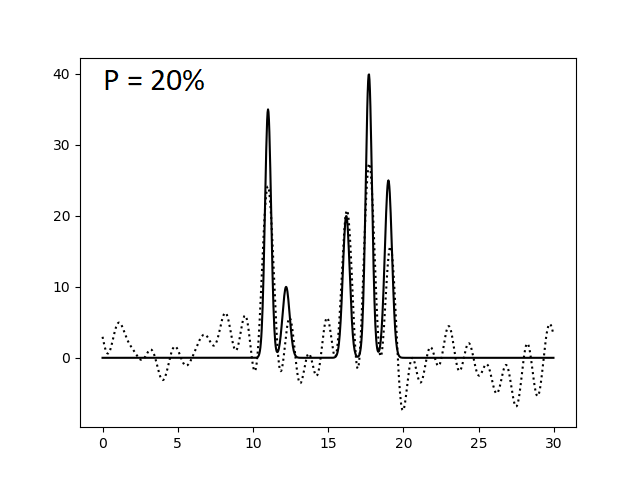
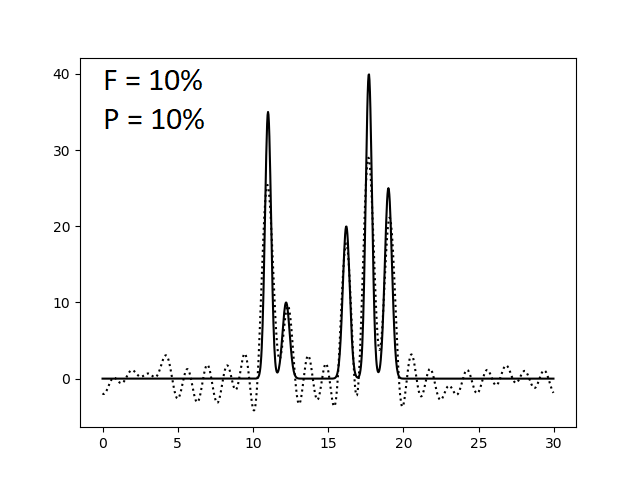
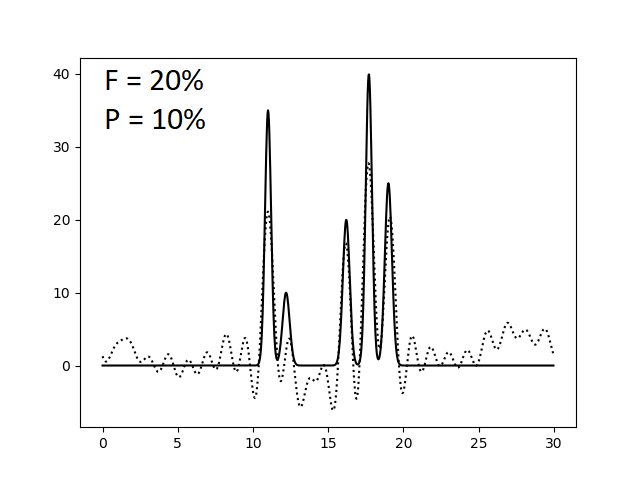
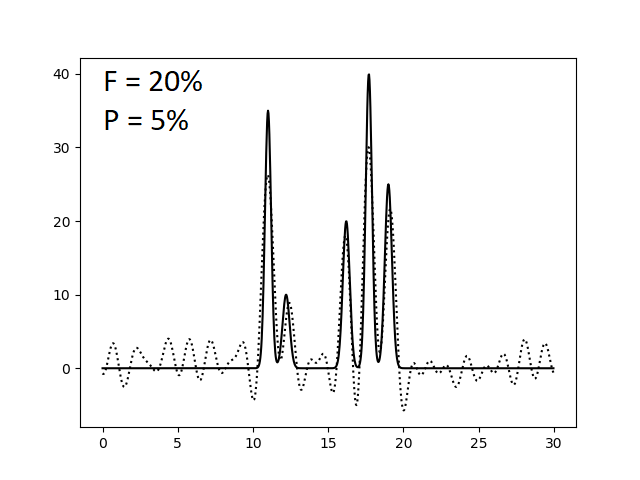
При сравнении этих изображений видно, что уже 40% шум по амплитудам и 20% шум по фазам сильно усложняют выявление атомов, делая некоторые сигналы "невидимыми" и сравнимыми с уровнем шума. Также заметим, что погрешности в фазах существеннее и быстрее портят картину, то есть амплитуда - более устойчивый к вариации параметр, чем фаза. Это же подтверждают последние три картинки, где некоторые атомы становятся неразришимыми при увеличении уровня шума по амплитудам на 10% (при фиксированном P), когда такой же эффект достигается при увеличении уровня шума по фазам всего лишь на 5% (при фиксированном F).

Восстановление функции электронной плотности по неполным наборам гармоник

На следующем этапе было интересно оценить качество восстановления функции электронной плотности на неполных наборах гармоник. Сперва я из набора от 0 до 23 гармоники удалила первые две. По картинке ниже видно, что базовая линия приобрела очертания синусоиды. Тем не менее, если сделать на это поправку, то все атомы удастся идентифицировать.

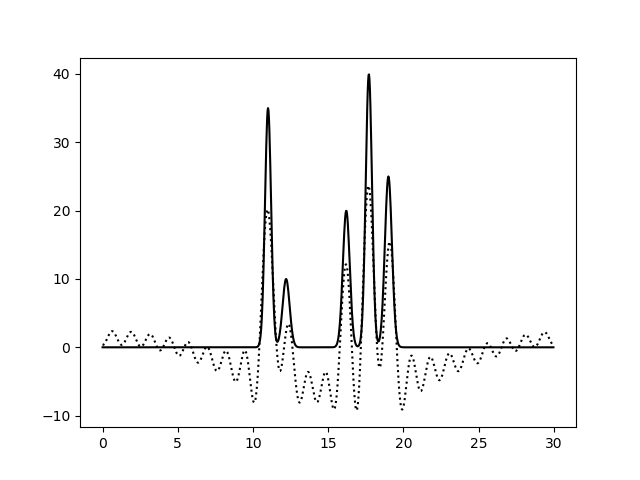
Затем я из середины полного набора удалила две случайно выбранные гармоники (8 и 14). Ниже приведена получившаяся картинка, в которой хоть шум и стал сильнее, но все равно пики очень четко выделяются.

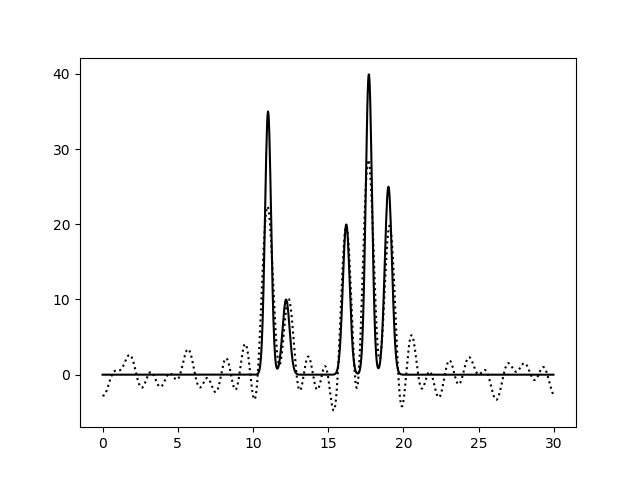
Далее я решила посмотреть, что получится, если к полному набору гармоник добавить еще одну с номером больше, чем N = 23. Понятно, что чем больше ее порядковый номер, тем менее существенным будет вносимый вклад в аппроксимацию, поэтому в качестве такой добавочной гармоники я взяла 25-ю. Ниже слева представлено получившееся восстановление функции, а справа - референс. Разница практически не заметна. Видно лишь небольшое снижение шума ближе к правому концу графика. Добавление более дальней гармоники (65-й) тоже не показало существенных изменений в качестве восстановления (данные не приведены).

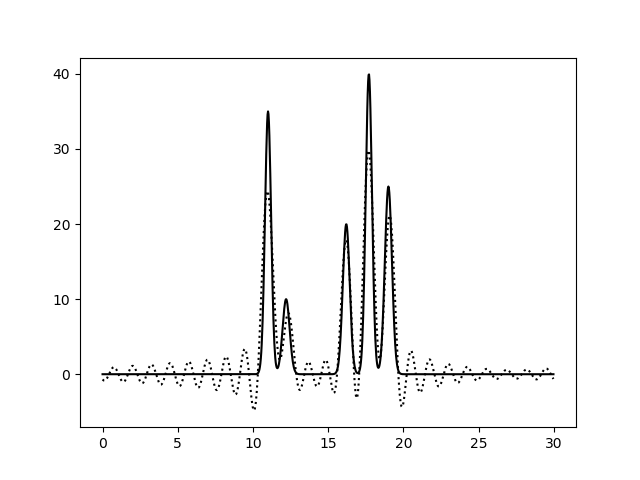
Теперь я попробовала удалить побольше гармоник из середины набора (10..15), в результате чего, получила среднее по качеству восстановление, в котором есть шумовые пики сопоставимые по уровню с сигналом.

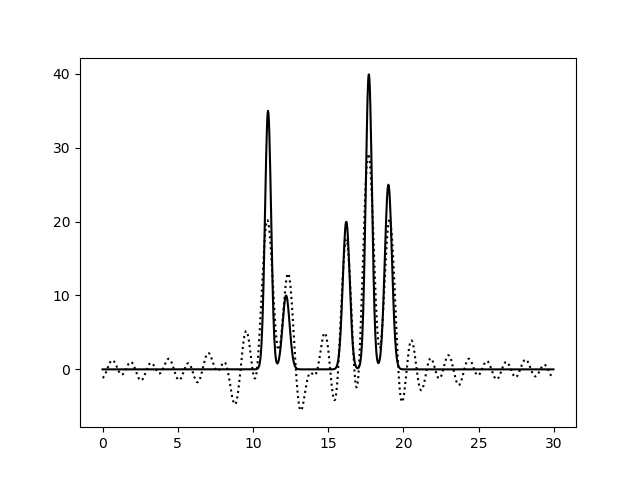
Если же наоборот оставить в наборе только средние гармоники (5..20), то картина окажется совершенно неразрешимой. Скорее всего из-за того, что первые гармоники во многом задают положение молекул на отрезке, а последующие все больше и больше уточняют модель вплоть до отдельных атомов. Поэтому отсутствие ключевых гармоник так критично.

Ниже представлена сводная таблица с результатами восстановления функции электронной плотности в рамках компьютерной модели из двух молекул и пяти атомов по полному и неполному наборам гармоник, а также с добавлением погрешности определения коэффициентов ряда Фурье.

Таблица 1. Восстановление функции электронной плотности по коэффициентам ряда Фурье
Набор гармоник	Разрешение (Å)	Полнота данных (%)	Шум амплитуды (% от F)	Шум фазы (% от phi)	Качество восстановления
Полный набор гармоник
0	-	100	0	0	-
0..10	3	100	0	0	плохое
0..20	1.5	100	0	0	среднее
0..22	1.36	100	0	0	хорошее
0..23	1.3	100	0	0	отличное
0..30	1	100	0	0	отличное
0..40	0.75	100	0	0	отличное
0..50	0.6	100	0	0	отличное
0..23	1.3	100	20	0	отличное
0..23	1.3	100	30	0	хорошее
0..23	1.3	100	40	0	среднее
0..23	1.3	100	0	10	отличное
0..23	1.3	100	0	15	хорошее
0..23	1.3	100	0	20	среднее
0..23	1.3	100	10	10	отличное
0..23	1.3	100	20	10	среднее
0..23	1.3	100	20	5	отличное
Неполный набор гармоник
2..23	1.3	91.7	0	0	отличное
0..7 9..13 15..23	1.3	91.7	0	0	хорошее
0..23 25	1.3	96.2	0	0	отличное
0..9 16..23	1.3	75	0	0	среднее
5..20	1.5	76.2	0	0	плохое

Для справки привожу критерии качества восстановления функции по сравнению с исходной