Алгоритмы и программы множественного выравнивания
Алгоритм сравнения разных выравниваний одних и тех же последовательностей
С помощью языка программирования Python был написан алгоритм сравнения разных выравниваний ождинх и тех же последовательностей. По ссылке доступен код в GoogleColab. Его можно скачать (в левом верхнем углу: File -> Download -> Download .py) и пользоваться в командной строке (информацию о запуске можно посмотреть введя в командную строку python sovpad.py -h).
Сравние выравниваний одних и тех же последовательностей тремя разными программами Mafft, Muscle, Tcoffee
Для выполнения данного задания были взяты последовательности из предыдущего практикума, а именно семейство белков из Pfam с AC: PF04820. Сравнивались программы: Mafft и Muscle, Mafft и Tcoffee. Выравнивания были сделаны в JalView (файл).
Сравнение Mafft и Muscle
Применив алгоритм для сравнения выравниваний, я получил большое количество одинаково выровненных колонок (рисунок 1). Кроме того видно, что основную часть составляют именно одинаково выравненные блоки, а не отдельно взятые колонки (таблица 1).
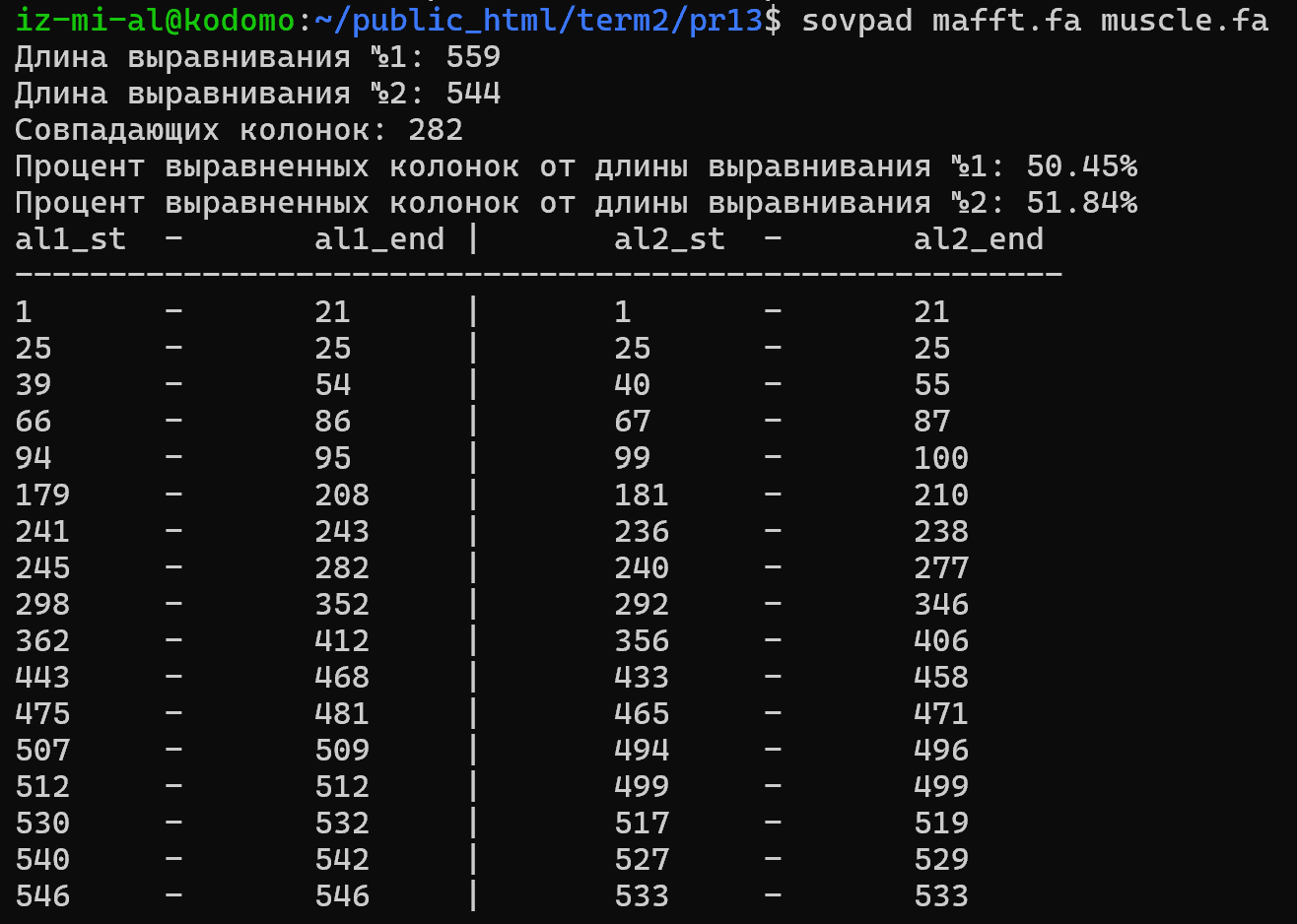
Одинаково выровненные колноки не вошедшие в блоки:
- (25,25)=(25,25)
- (512,512)=(499,499)
- (546,546)=(533,533)
| (s1,f1) | (s2,f2) | length |
|---|---|---|
| (1,21) | (1,21) | 21 |
| (39,54) | (40,55) | 16 |
| (66,86) | (67,87) | 21 |
| (94,95) | (99,100) | 2 |
| (179,208) | (181,210) | 30 |
| (241,243) | (236,238) | 3 |
| (245,282) | (240,277) | 38 |
| (298,352) | (292,346) | 55 |
| (362,412) | (356,406) | 51 |
| (443,468) | (433,458) | 26 |
| (475,481) | (465,471) | 7 |
| (507,509) | (494,496) | 3 |
| (530,532) | (517,519) | 3 |
| (540,542) | (527,529) | 3 |
Сравнение Mafft и Tcoffee
Применив алгоритм для сравнения выравниваний, я также получил большое количество одинаково выровненных колонок, но всё же немного меньше, чем в предыдущем случае (рисунок 2). Кроме того видно, что основную часть также составляют именно одинаково выравненные блоки, а не отдельно взятые колонки (таблица 2).
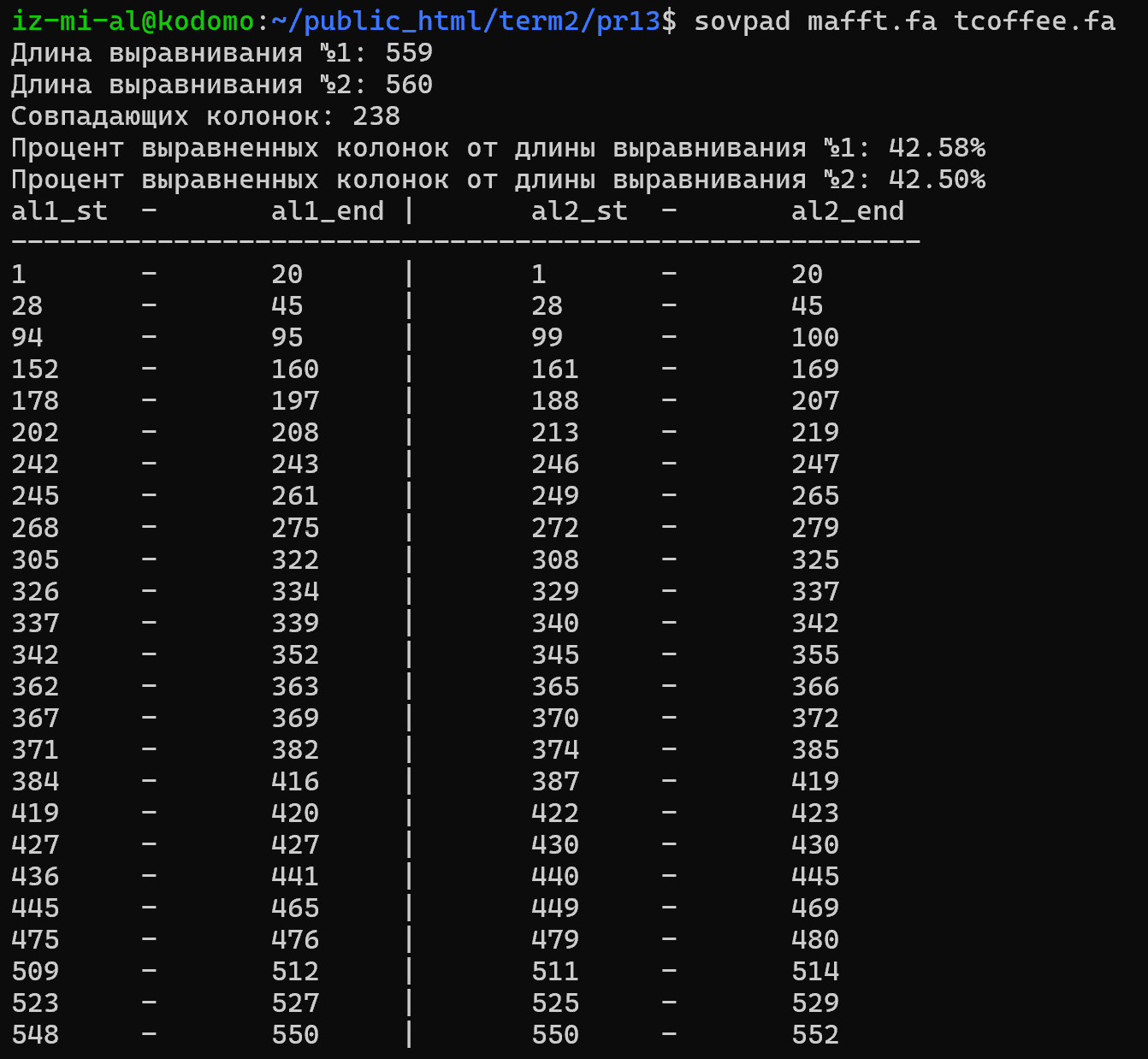
Одинаково выровненные колноки не вошедшие в блоки:
- (427,427)=(430,430)
| (s1,f1) | (s2,f2) | length |
|---|---|---|
| (1,20) | (1,20) | 20 |
| (28,45) | (28,45) | 18 |
| (94,95) | (99,100) | 2 |
| (152,160) | (161,169) | 9 |
| (178,197) | (188,207) | 20 |
| (202,208) | (213,219) | 7 |
| (242,243) | (246,247) | 2 |
| (245,261) | (249,265) | 17 |
| (268,275) | (272,279) | 8 |
| (305,322) | (308,325) | 18 |
| (326,334) | (329,337) | 9 |
| (337,339) | (340,342) | 3 |
| (342,352) | (345,355) | 11 |
| (362,363) | (365,366) | 2 |
| (367,369) | (370,372) | 3 |
| (371,382) | (374,385) | 12 |
| (384,416) | (387,419) | 33 |
| (419,420) | (422,423) | 2 |
| (436,441) | (440,445) | 6 |
| (445,465) | (449,469) | 21 |
| (475,476) | (479,480) | 2 |
| (509,512) | (511,514) | 4 |
| (523,527) | (525,529) | 5 |
| (548,550) | (550,552) | 3 |
Обсуждение результатов
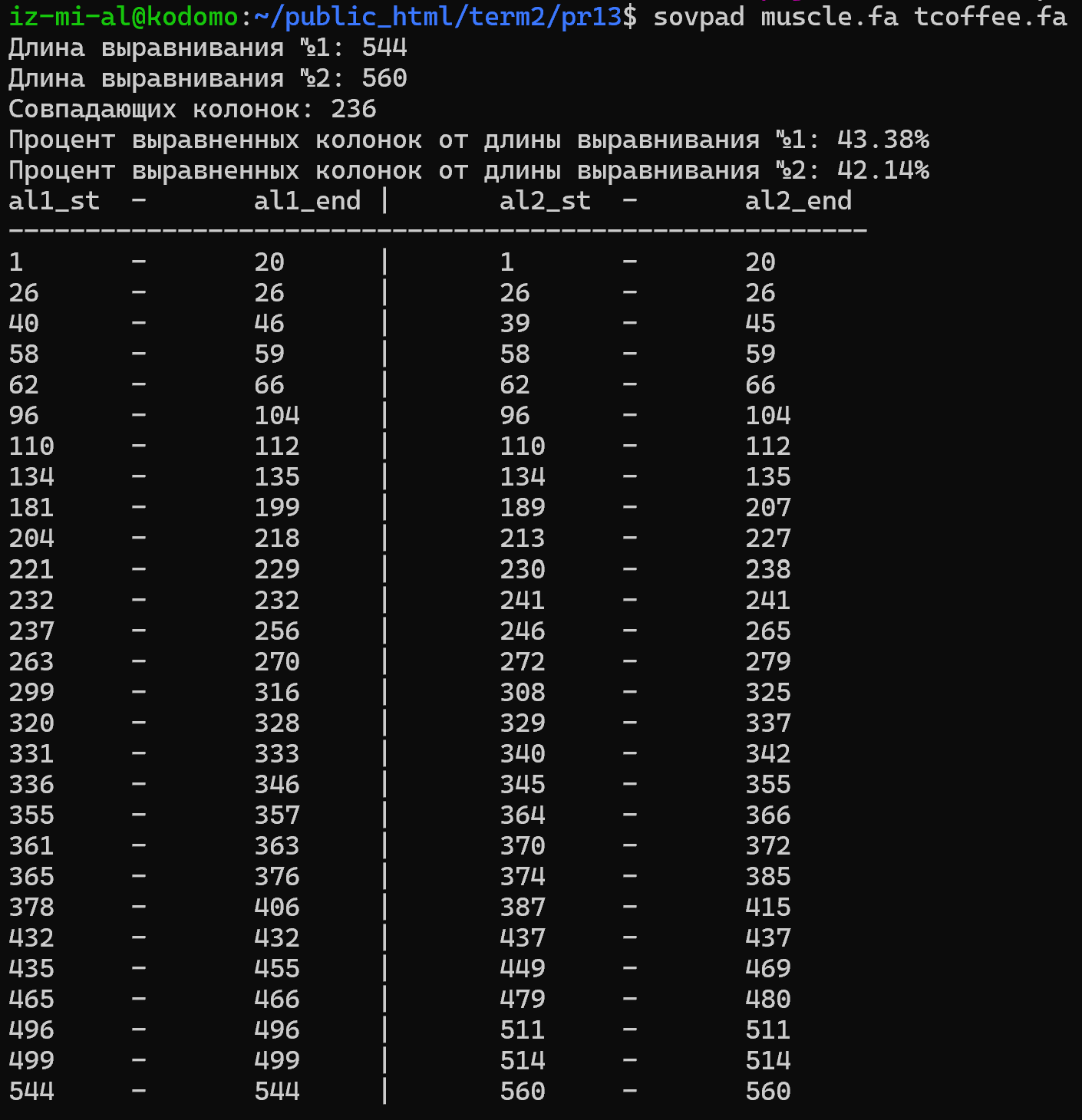
Если выделить самые крупные участки совпадения из каждого из сравнений, то можно увидеть какие блоки были найдены и с помощью Muscle, и с помощью Tcoffe, что может свидетельствовать о консервативности данных участков (то есть такой блок получен в каждом из 3 выравниваний). Такими участками являются (колонки приведены в порядке Mafft-Muscle-Tcoffee):
- (1,20)=(1,20)=(1,20)
- (39,45)=(40,46)=(39,45)
- (179,197)=(181,199)=(189,207)
- (202,208)=(204,210)=(213,219)
- (245,261)=(240,256)=(249,265)
- (268,275)=(263,270)=(272,279)
- (305,322)=(299,315)=(308,325) - большая вероятность делеции в последовательности Q9A4M4_CAUVC
- (326,334)=(320,328)=(329,337)
- (371,383)=(365,377)=(374,385) - большая вероятность вставки в последовательностях Q8KLM2_STRTO и Q6ZZI5_ACTTV7
- (384,412)=(378,406)=(387,415)
- (445,465)=(435,455)=(449,469)
Все данные блоки с очень большой вероятностью в действительности выровнены правильно, так как их сопоставили между собой все 3 программы.
Можно убедиться в наличии совпдающих блоков, посмотрев выравнивание скачав файл JalView.
Построение выравнивания по совмещению структур и сравние его с выравниванием программой MSA
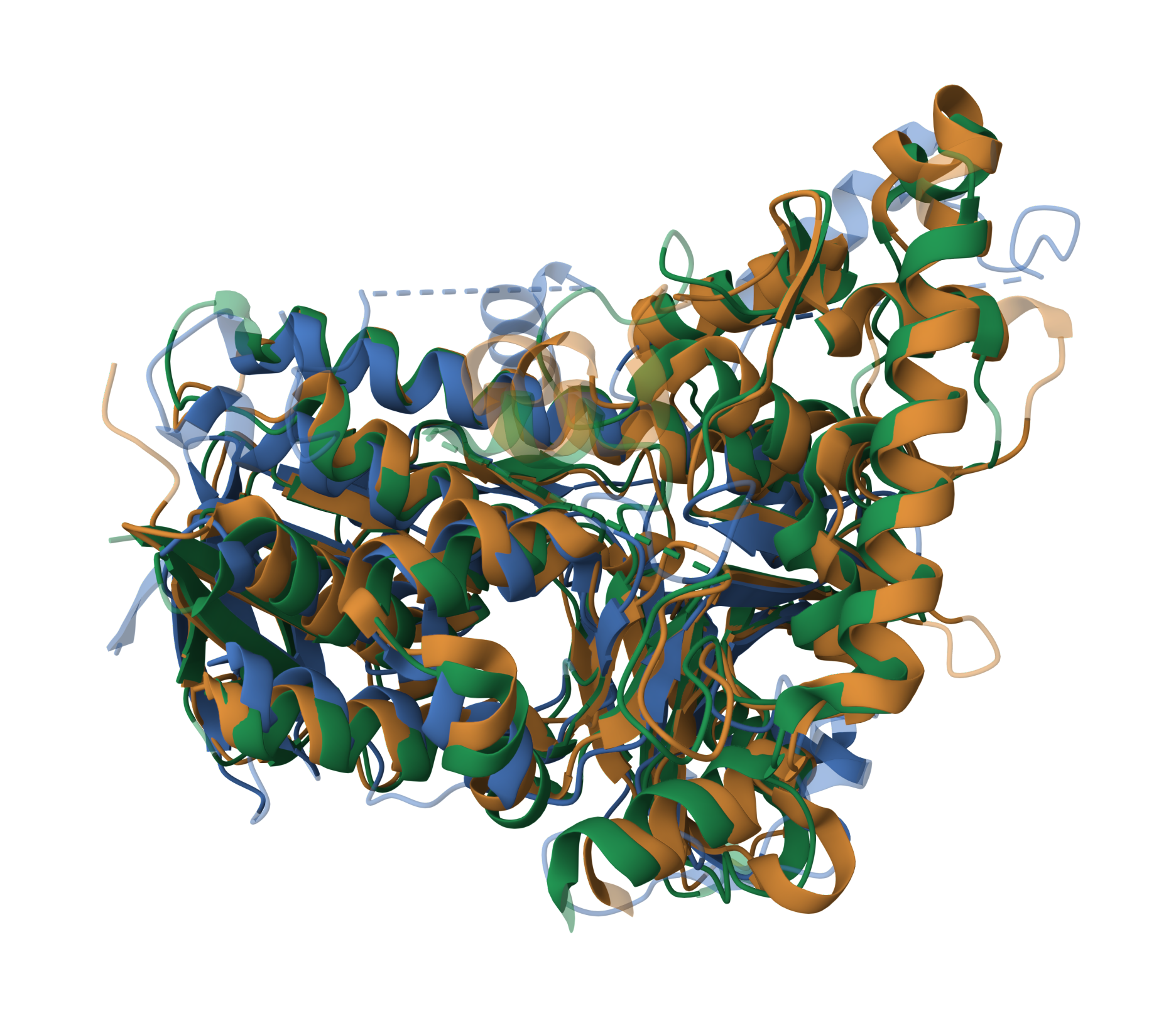
Из выбранного мною семейства белков, было выбрано 3 с известной структурой, а именно белки с ID: 2APG, 3E1T, 6NSD. Было сделанно парное выравнивание с помощью программы из PDB белков 2APG с 3E1T и 2APG с 6NSD. Затем самостоятельно было сделанно множественное выравнивание. Также было сделанно выравнивание этих трёх последовательностей с помощью программы MSAprobs. Было проведенно сравнение (рисунок 4).
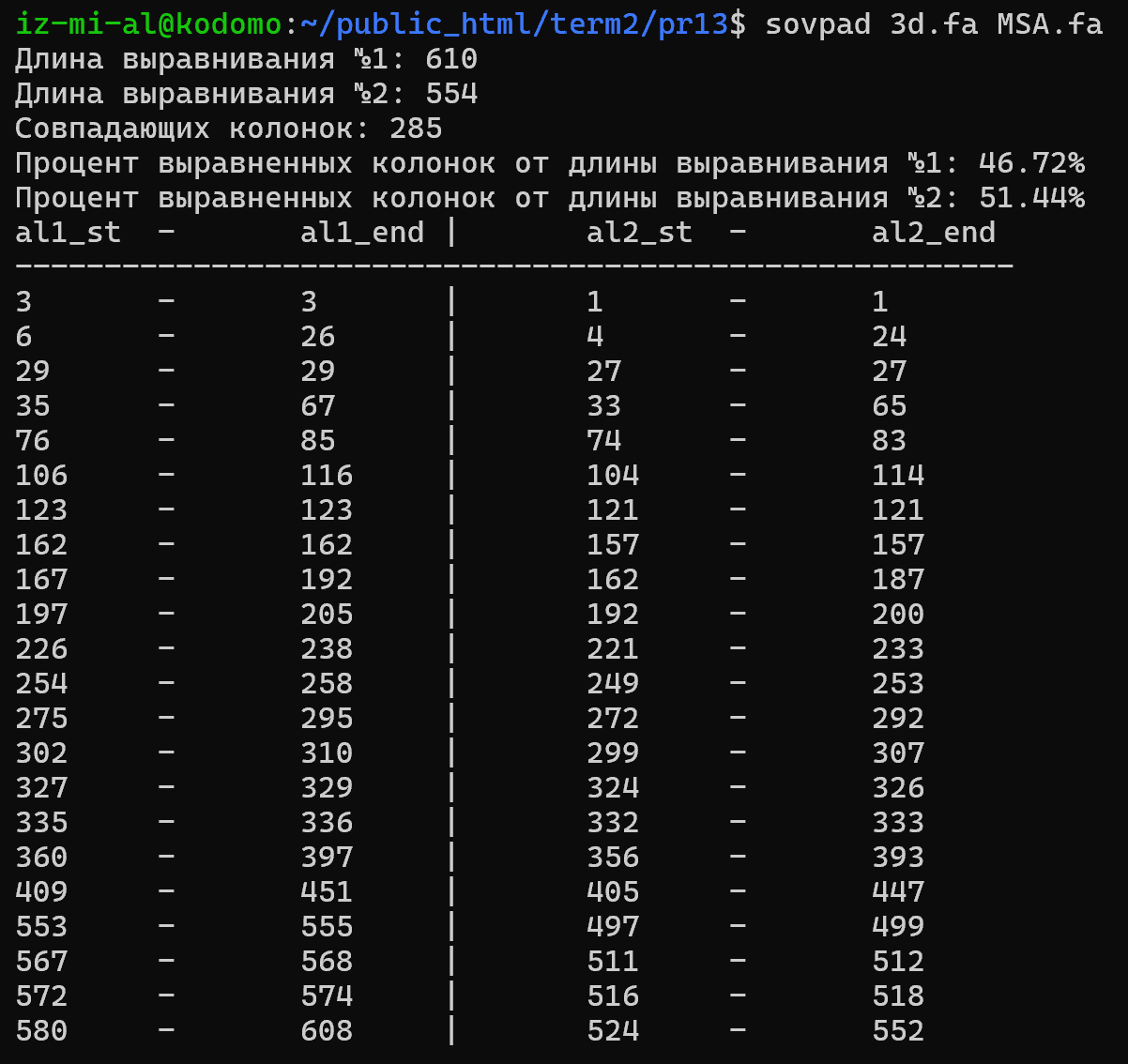
Почти все выровненные колонки входят в блоки, кроме трёх: (3,3)=(1,1), (29,29)=(27,27) и (123,123)=(121,121).
Выравнивания можно посмотреть скачав файл. Наложение пространственных структур белков приведенно на рисунке 5 (жёлтый - 2APG, синий - 3E1T, зелёный - 6NSD).
Описание команды T-Coffee[1]
T-Coffee - прогрессивный метод множественного выравнивания последовательностей. Он был выпущен в свет в 2000 году и позволил повысить точность для отдалённо связанных последовательностей, несильно теряя во времени. Данный метод основан на построении всех возможных попарных выравниваний. По полученным данным строится библиотека, которая затем используется для построения множественного выравнивания.
В отличии от предыдущих существовавших методов, T-Coffee, создавая выравнивание, не просто добавляет к уже выровненным последовательностям (например к двум первоначальным A и B) следующую последовательность (например C), тем самым подравнивая её (C) к уже выровненным (A и B), а также сверяет, как новая последовательность (C) соотносится с каждой уже выровненной (отдельно с A и отдельно с B). Благодаря этому уменьшается число локальных ошибок, так как уже выровненная часть может редактироваться в зависимости от следующей добавляемой последовательности. Таким образом, T-Coffee принимает решение на основе полной картины, а не просто подравнивает следующую последовательность к уже выровненным.