Algorithms Trees Reconstruction

Задание 1. Укоренение в среднюю точку.

Мы уже знаем, что укоренять дерявья в среднюю точку, построенные методом UPGMA, не имеет смысла, потому что все они ультраметрические и укорененные. В то время как этом имеет смысл делать для деревьев, у которых указаны длины ветвей и нет корня. При укоренении таким методом, предполагая равные темпы эволюции всех ветвей дерева, корень помещаем по середине самого длинного "маршрута".

Укореним в среднюю точку дерево, построенное при выполнении предыдущего занятия методом neigbour joining tree using PID. Для этого воспользуемся программой retree пакета PHYLIP.

  • Скопируем файл с деревом в Newick-формате в файл с именем intree;
  • Запустим retree;
  • Вызовем help для справки:


  • Далее выполним необходимые команды для укоренения в среднюю точку ("Midpoint root the tree") - М, и записи получившегося дерева в файл - W.
  • Выходному файлу outtree добавим расширение и откроем его программой MEGA:

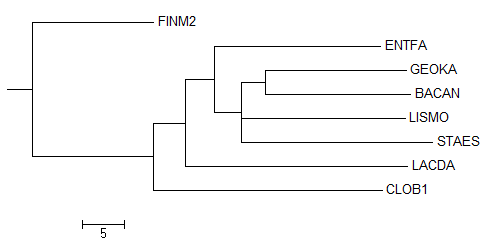
Neigbour joining tree using PID Верное дерево
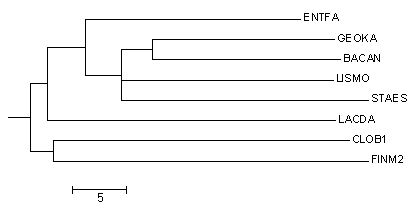
Дерево, укорененное в среднюю точку программой retree пакета PHYLIP.

Укоренение произошло в правильное место. Кроме того, дерево стало более ровным, потому что из-за метода самые длинные ветви подравниваются (а остальные встают как получилось). Верные разбиения (нетривиальные ветви) не измнеились (но приведем их для ясности):

  • {BACAN,GEOKA} vs {CLOT1,FINM2,STAES,LISMO,LACDA,ENTFA};
  • {CLOT1,FINM2} vs {BACAN,GEOKA,STAES,LISMO,LACDA,ENTFA};
  • {BACAN,GEOKA,STAES,LISMO} vs {CLOT1,FINM2,LACDA,ENTFA}.

Задание 2. Использование внешней группы.

Метод максимальной экономии (maximum parsimony), направленный на анализ данных о последовательностях, определяет оптимальное дерево так, чтобы минимизировать колличество мутаций. При этом как таковых расстояний между листьями нет, поэтому не возможно выбрать самый длинный маршрут и произвести укорените в среднюю точку.

Однако можно воспользоваться укоренением с помощью внешней группы. Это можно сделать, используя в качестве внешней группы белок того же семейства из другой бактерии (в нашем случае - из кишечной палочки Escherichia coli, ECOLI). Все отобранные бактерии - Firmicutes (грамположительные), а ECOLI относится к Proteobacteria (грамотрицательные). Таксономия: 

 Bacteria; Proteobacteria; Gammaproteobacteria; Enterobacteriales; Enterobacteriaceae; Escherichia.

Добавим к файлу с невыровненными последовательностями белков фирмикут последовательность белка из кишечной палочки, после чего выровняем их вместе (выравнивание в fasta-формате). Импортируем выравнивание, полученное muscle в программу MEGA и построим дерево Maximum parsimony.

Далее Subtree=>Root=>ветвь, ведущая к ECOLI=>Show Subtree Separately (изображение голубой лупы на фоне дерева на левой панели окна MEGA):


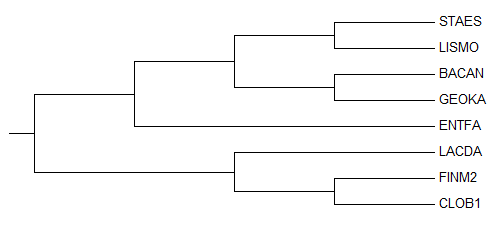
Так как расстояния не учитываются, но учитывается относительное количество мутаций, листья все на одном расстоянии от корня. Построенное дерево уже гораздо сильнее отличается от правильного. Есть три верных разбиения (нетривиальных ветвей):

  • {BACAN,GEOKA} vs {CLOT1,FINM2,STAES,LISMO,LACDA,ENTFA};
  • {CLOT1,FINM2} vs {BACAN,GEOKA,STAES,LISMO,LACDA,ENTFA};
  • {BACAN,GEOKA,STAES,LISMO} vs {CLOT1,FINM2,LACDA,ENTFA}.

Это три из пяти. Следовательно, я думаю, можно считать такое дерево среднедостоверным (на 60%).

Задание 3.Bootstrap analysis

Проведем бутстрэп-анализ филогении белков, используя один из методов, доступных из программы MEGA. Для этого в окошке, которое открывается после вызова программы (при построении UPGMA дерева), в меню "Test of Phylogeny" выберем "Bootstrap method". Число реплик выберем 100. Чтобы получить число и для ветви к листу FINM2, пришлось выравнивать с кишечной палочкой:


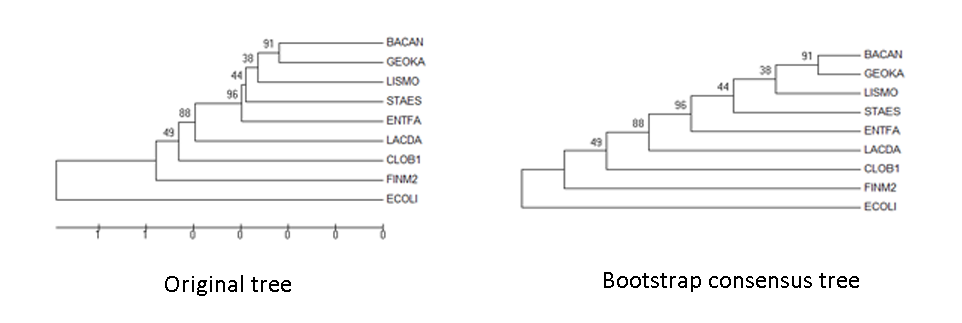
Деревья "Original tree" и "Bootstrap consensus tree" не отличаются. Это говорит о том, что построение по части данных (100 реплик по случайной половине имеющихся столбцов выравнивания) в принципе такое же по достоверности (в данном случае, не очень достоверное), как и по полноценным данным. Если я правильно поняла, то укорениться такое дерево должно около числа 96, что не соответсвует верному укоренению.



Наверх