Занятие 3. Восстановление функции по коэффициентам её ряда Фурье

Главная
Исследования качества восстановления функции одной переменной в зависимости от того, какие и сколько гармоник ряда Фурье используются для ее восстановления.

1.Полные наборы гармоник

Выбрала модель для компьютерного эксперимента на отрезке от 0 до 30 ангстрем: первая молекула,5 атомов: N,C,B,H,O и вторая,6 атомов: O,N,O,H,N,C.
Функция задается на интервале [0,30]. Моделируется в 1D график электронной плотности молекулы. 30 следует понимать как 30 ангстрем. Функция имеет вид нескольких гауссовых кривых с центром в разных точках.
Функцию можно создать с помощью скрипта compile-func.py. Гауссова функция определяется числами lambda,beta,gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2). Здесь a^2=a*a.
Скрипт для построения функции:
python compile-func.py –g 30,3,3+32,3,4.3+25,3,5.5+2,3,6.8+35,3,8+35,3,12+30,3,13.3+35,3,14.5+2,3,15.7+30,3,17+32,3,18.2
Изображение графика функции, которое выдает скрипт.

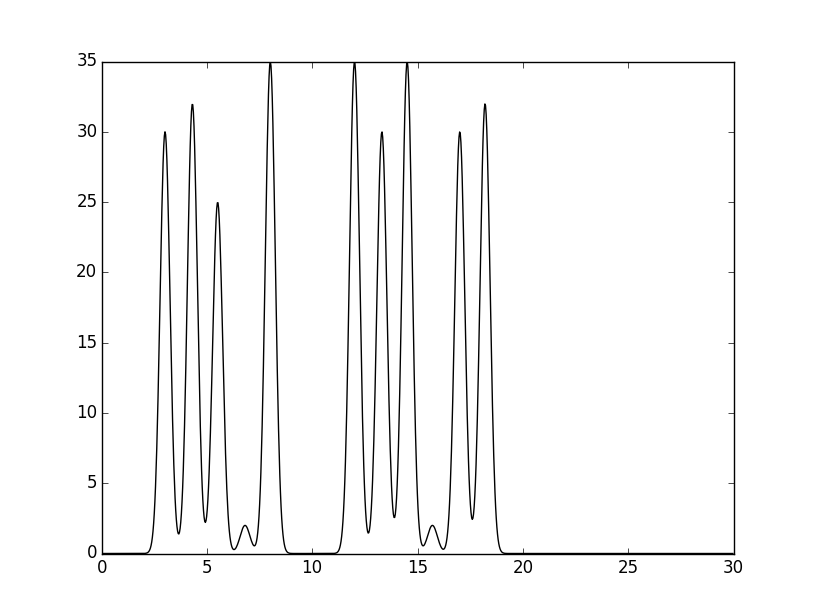
Коэффициенты Фурье рассчитываются с помощью скрипта func2fourier.py:
python func2fourier.py –i func.txt
Получила файл с коэффициентами Фурье соответствующей функции func_ft.txt.
Затем требовалось найти номер гармоники, с которой начинается отличное восстановление, я решила начать с номера 10. Использовала команду:
python fourier-filter.py –r 0-10
Получила график. Видно,что качество плохое.

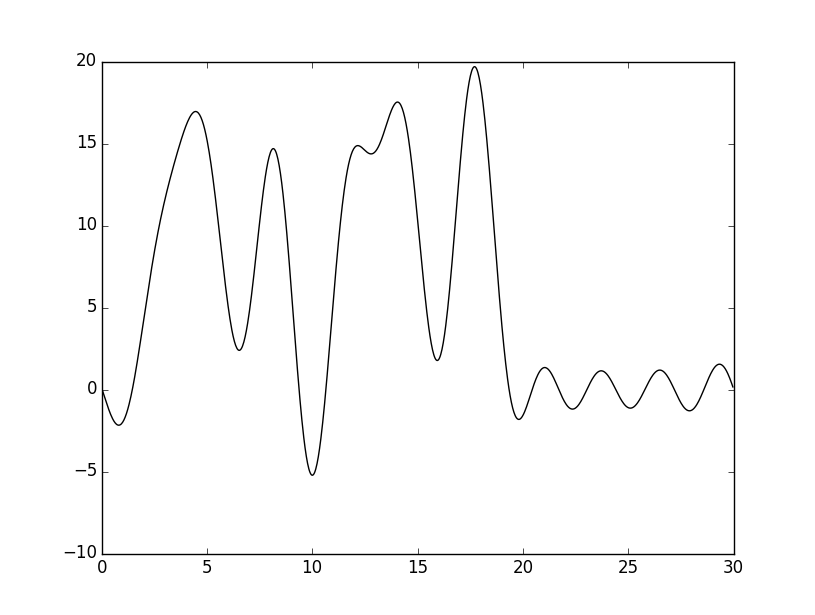
Поэтому продолжила для 20:
python fourier-filter.py –r 0-20

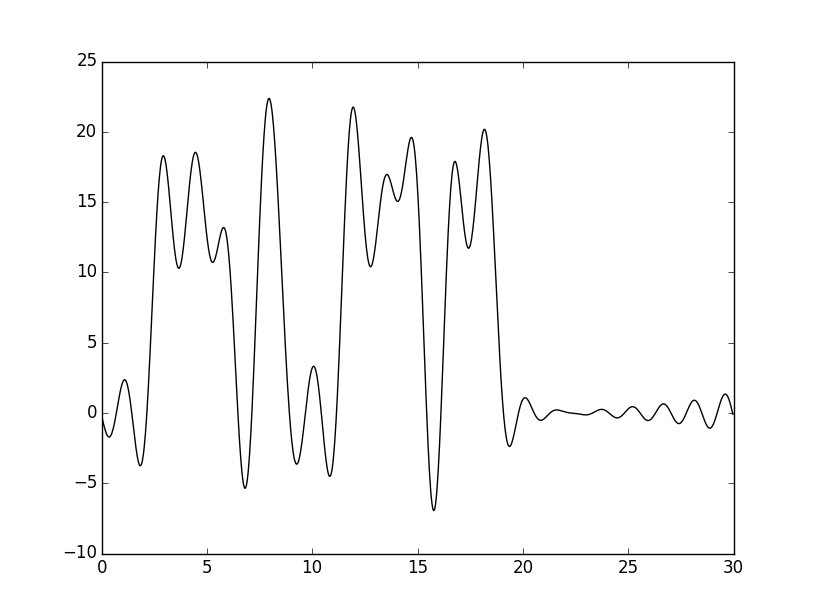
Полученное изображение. Качество не отличное, поэтому сделала для 30:
python fourier-filter.py –r 0-30

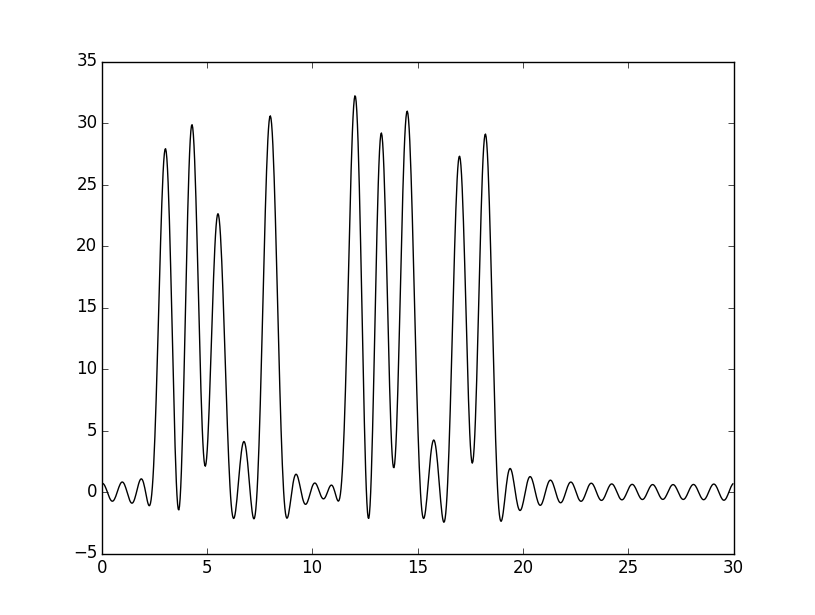
Получила изображение. Здесь уже можно говорить об отличном восстановлении.
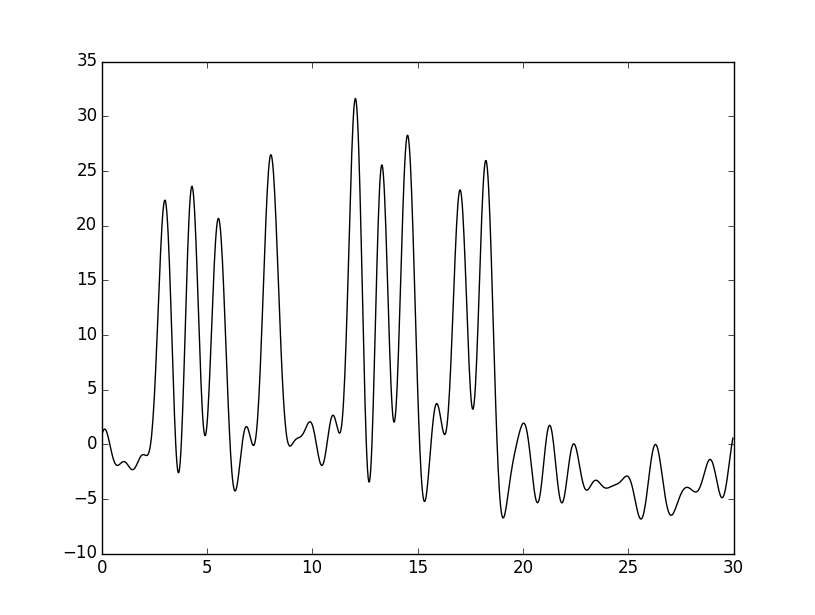
Далее добавила 20% шума к структурным факторам и 10% шума к фазам с помощью команды:
python func2fourier.py –i func.txt –F 20 –P 10
Получила изображение. Видим, что качество ухудшилось до хорошего.

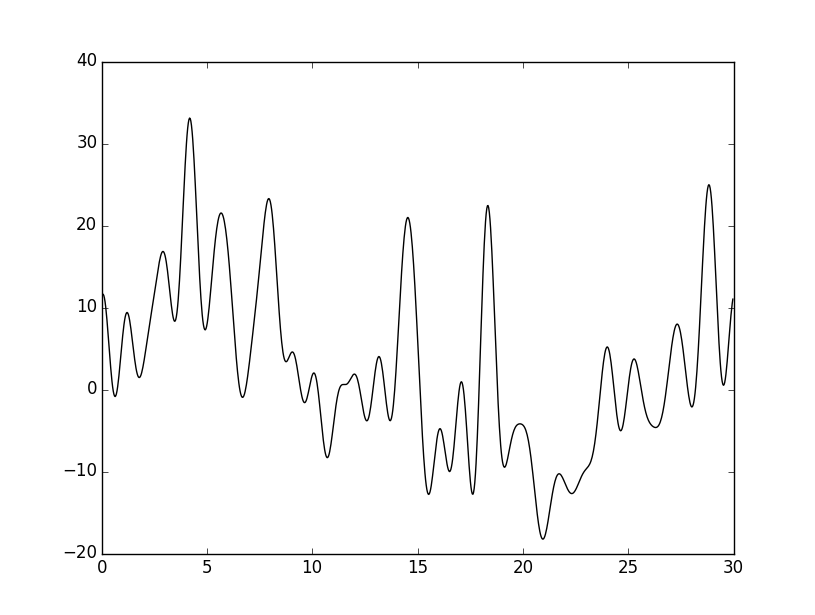
Затем добавила 70% шума к структурным факторам и 50% шума к фазам с помощью команды:
python func2fourier.py –i func.txt –F 70 –P 50

Получила изображение. Видим, что качество ухудшилось до плохого.

2.Неполные наборы гармоник

Удалила две начальные гармоники (номера 0-1) с помощью команды:
python fourier-filter.py –r 2-30
Получила изображение. Качество отличное.

Удалила 10% гармоник из середины набора(15,16,17):
python fourier-filter.py –r 0-14,18-30
Качество изображения снизилось до хорошего.

Добавила одну гармонику с номером, превышающим n_0 на 10 (т.е. 30 на 10, значит 40):
python fourier-filter.py –r 0-30,40
Качество изображения отличное (пунктиром изображена функция распределения для гармоник 0-30,40 , а сплошной линией для всех гармоник).

Правило для определения разрешения по набору гармоник:
На последнем примере- 0-30,40. Номер последней гармоники – 40, т.е. по идее разрешение должно быть 30/40=0.75 A. Но давайте посмотрим какая будет в данном случае полнота данных, если считать гармонику с номером 40 последней, грубо говоря –это 30/40,т.е.75%. А если ориентироваться на гармонику с номером 30, то разрешение будет 30/30 =1 А. Полнота данных в этом случай 100%,т.к. все гармоники до 30-й включительно присутствуют. Какое же тогда разрешение? 1 А или 0.75 А? Количество гармоник, которое обуславливает разрешение 1 А больше кол-ва гармоник, обуславливающих разрешение 0.75 А (100% лучше, чем 75%). Иными словами 1 гармоника с высоким номером не сможет обеспечить видимость деталей с высоким разрешением. Поэтому в данном случае, следует говорить, что данный набор гармоник дает разрешение 1 А.
Краткий план работы:
1)Построила график восстановленной функции по полному набору гармоник с n = 0, 1, .... ,498.
Нашла n_0 при котором восстановление отличное (0–30). Документировала результат, приведя графики для 3-4х n, включая n_0, и заполнив строчки таблицы 1 в протоколе по теме "Ряд Фурье".
2) Добавила шум к амплитудам и фазам при восстановлении по полному набору гармоник 0,...,30. Оценила качество восстановления в зависимости от шума, 3 результата внесла в протокол.
Неполные наборы гармоник
1) Удалила две начальные гармоники (номера 0-1). Результаты внесла в таблицу.
2) Удалила 10% гармоник из середины набора(15,16,17). Результаты внесла в таблицу.
3) Добавила одну гармонику с номером, превышающим n_0 на 10 (т.е. 30 на 10, значит 40). Результаты внесла в таблицу.
4) Предложила правило как определять разрешение для набора гармоник Фурье, по которым восстанавливается функция.
Таблица с результатами..