1. Модель для компьютерного эксперимента:
На отрезке [0,30] (Å) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1 Å друг от друга.
Молекулы расположены на расстоянии 5 Å. Всего 5 атомов. Электронные плотности (ЭП) атомов описываются гауссовой кривой.
Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.
Гауссова функция определяется числами lambda,beta,gamma по формуле:
gauss = lambda*exp(-(beta^2)*(X-gamma)^2).
Функцию задали с помощью скрипта compile-func.py с соответствующими параметрами:
python compile-func.py -g 40,3,4+35,3.5,6+2,3,8+9,3,15+28,3,20
Получилась сумма пяти гауссовых функций с max в точках 4, 6, 8, 15, 20 и высотой 32, 14, 2, 12 и 16, соответственно.
На выходе имеем текстовый файл func.txt с парами значений X и Y и график функции:
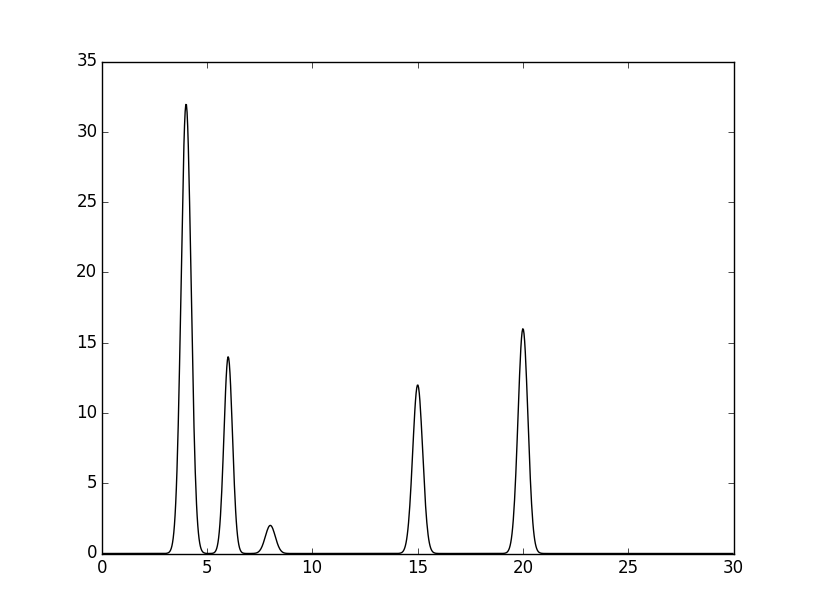
Рис.1 График заданной функции ЭП
2. Полные наборы гармоник
Коэффициенты Фурье рассчитали с помощью скрипта func2fourier.py
На вход дается функция в файле func.txt. Выходной файл func_ft.txt
содержит амплитуды и фазы гармоник с соответствующими номерами. Получилось 499 гармоник
Теперь проведем фильтрацию с помощью скрипта fourier-filter.py
и найдем n_0, при котором восстановление отличное
(т.е., при котором по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")).
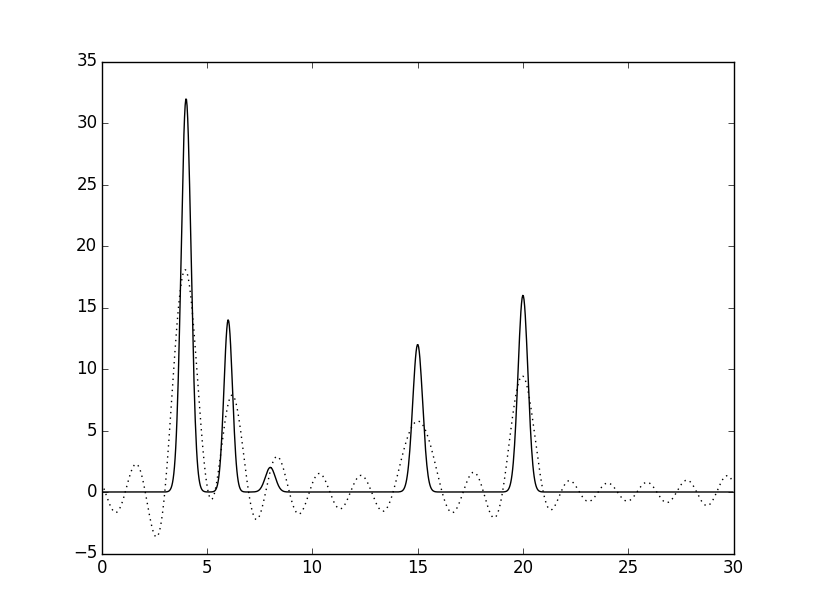
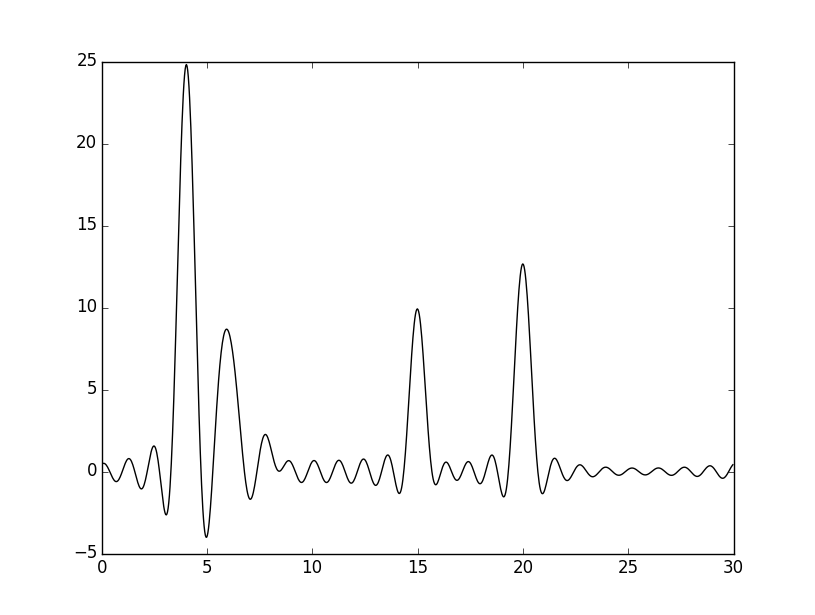
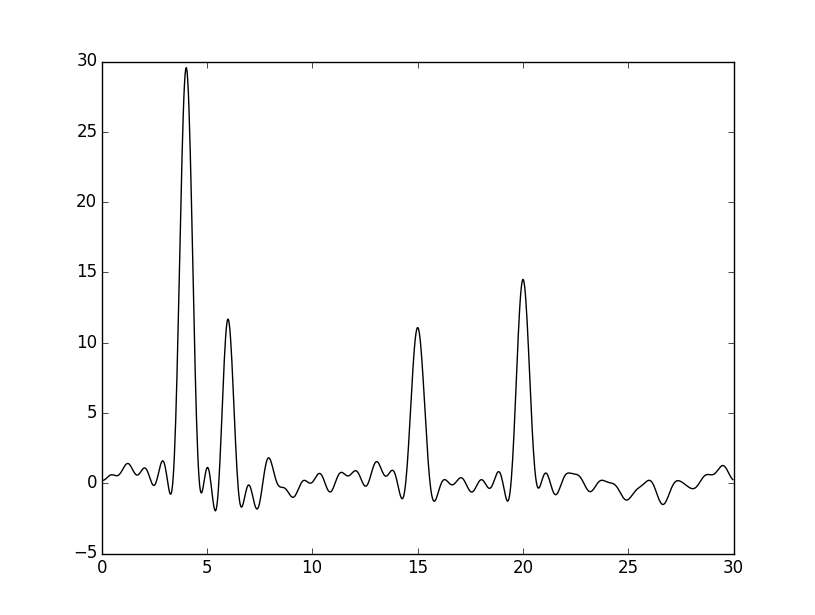
Ниже приведены результаты восстановления по полным наборам для четырех n: 15, 25, 30, 34. n_0 определено как 34.
 |  |
 |  |
 |  |
 | 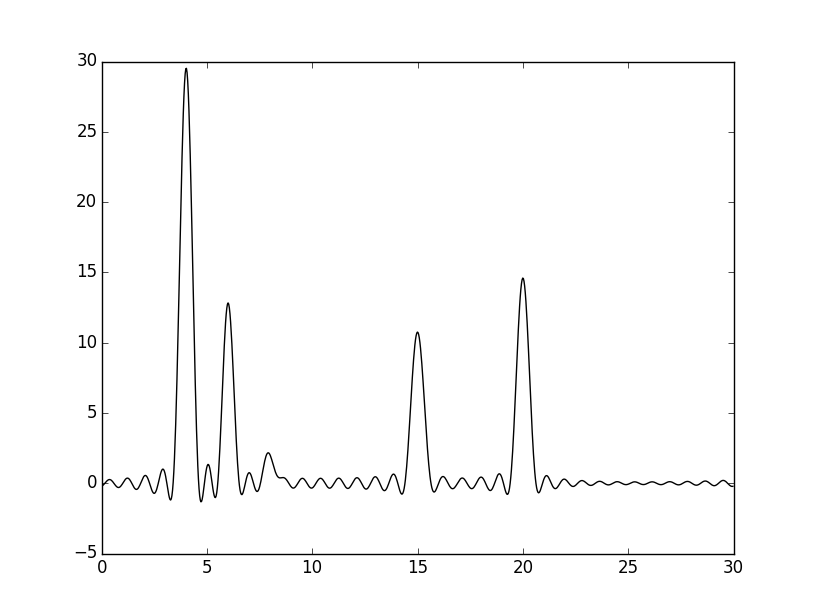 |
При n=15 и 25 восстановление можно назвать "средним": хорошо определяется положение четырех атомов. При n=30 восстановление "хорошее": можно было бы угадать положение и самого низкого пика, если бы было известно количество атомов. При n=34 восстановление можно назвать "отличным", определяются положения всех атомов.
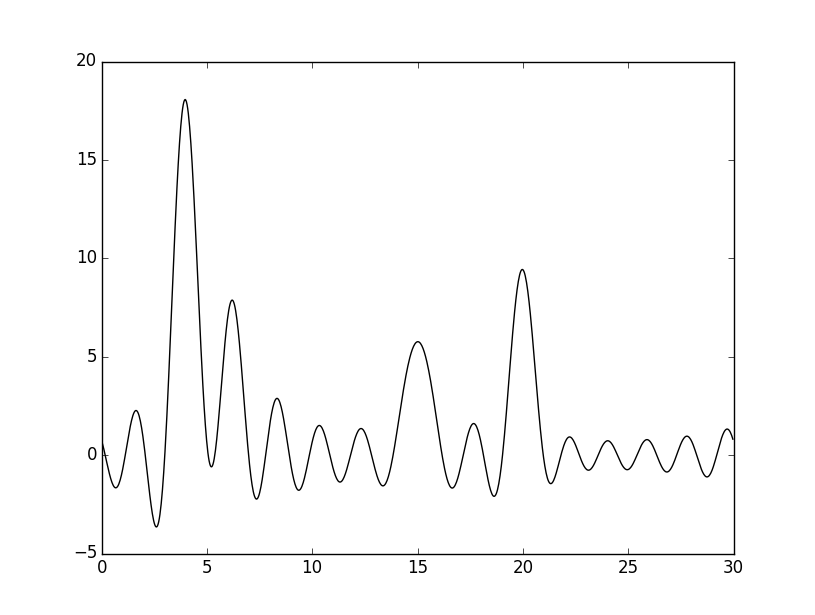
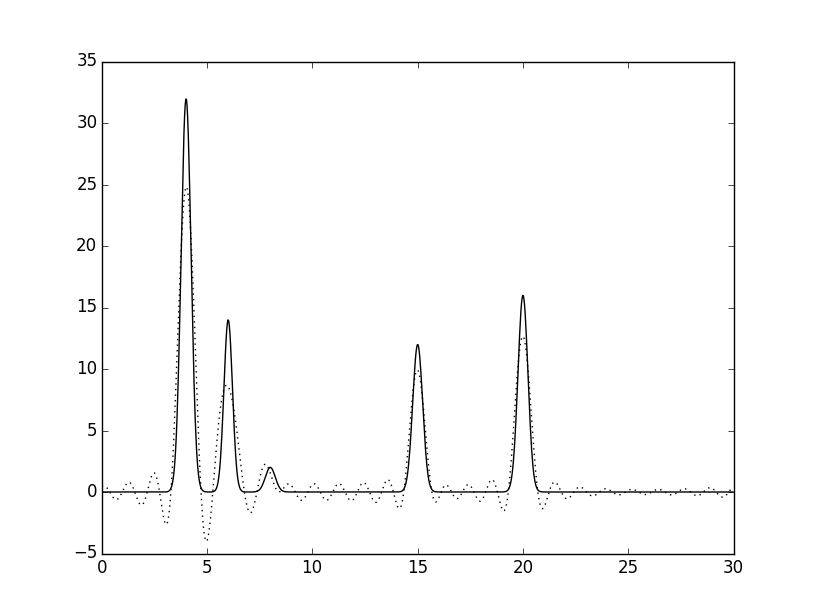
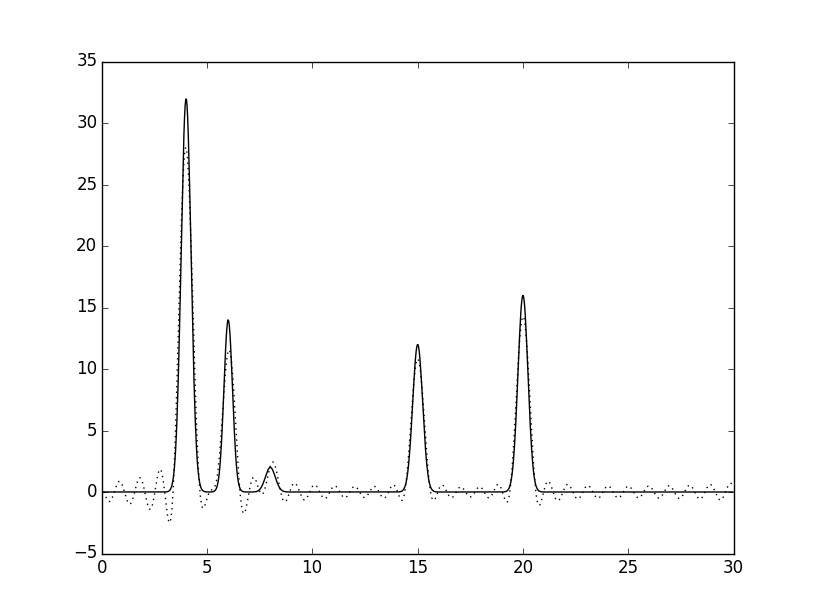
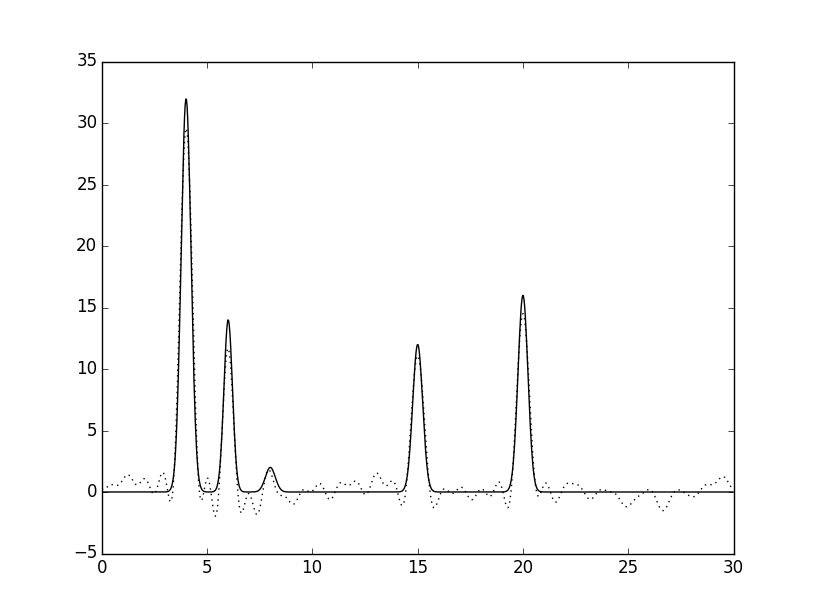
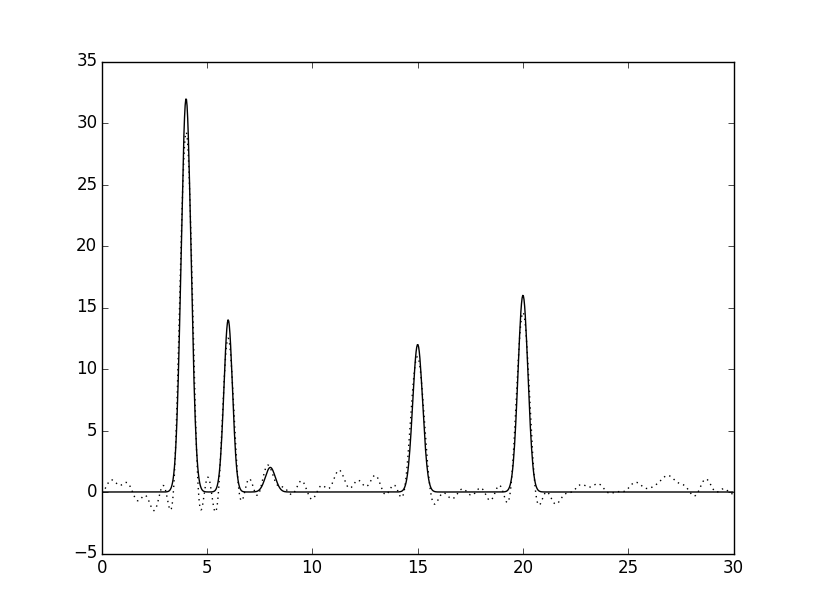
Далее был добавлен шум к амплитудам и/или фазам при восстановлении по полному набору гармоник 0,...,34: 1) 10% по φ, 2) 10% по F, 3) 15% по φ и F, 4) 20% по φ и F. Результаты приведены ниже.
 |  |
 | 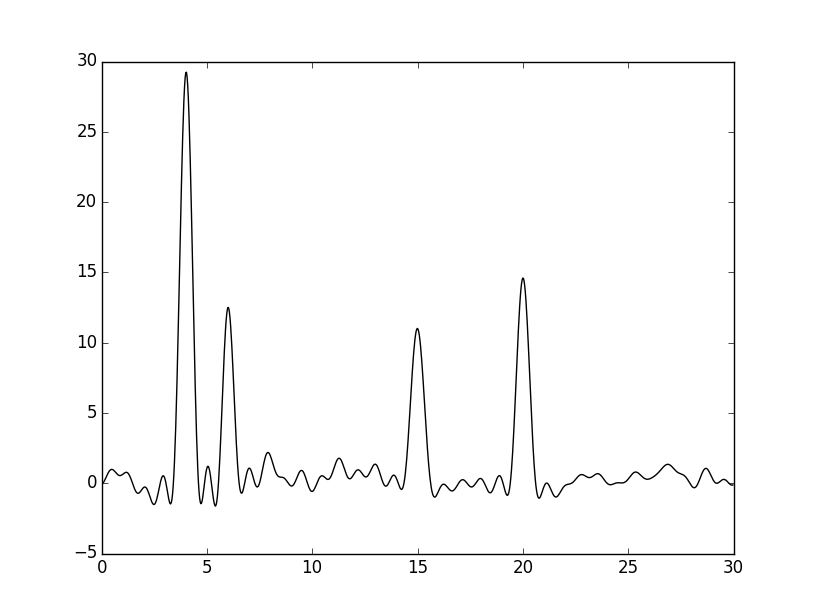 |
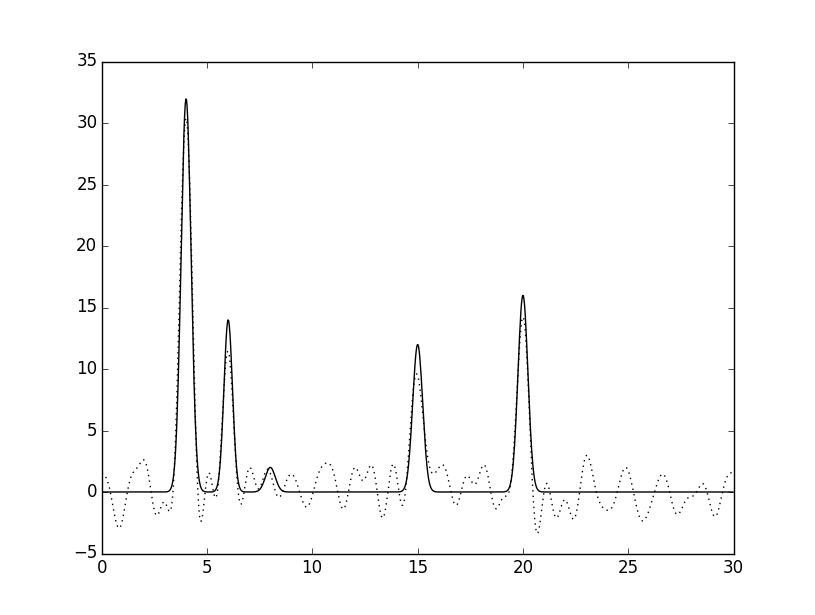 | 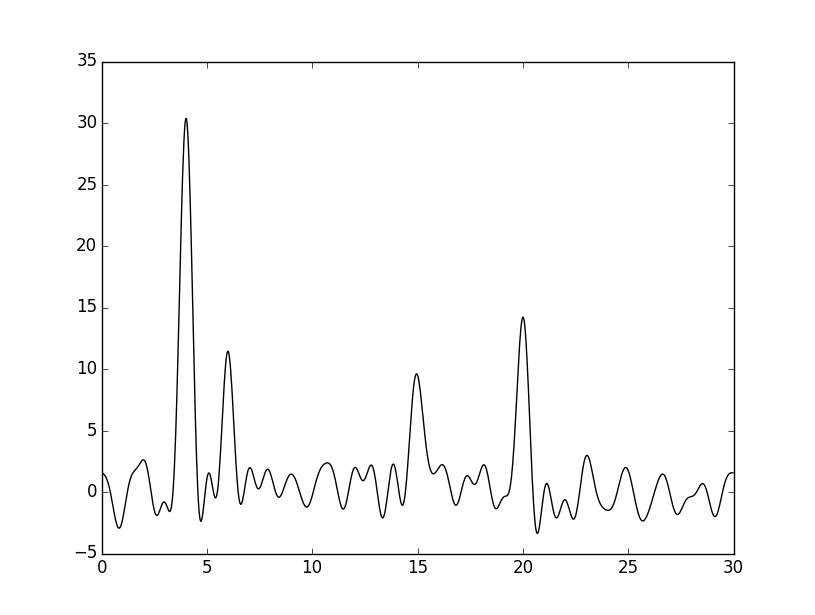 |
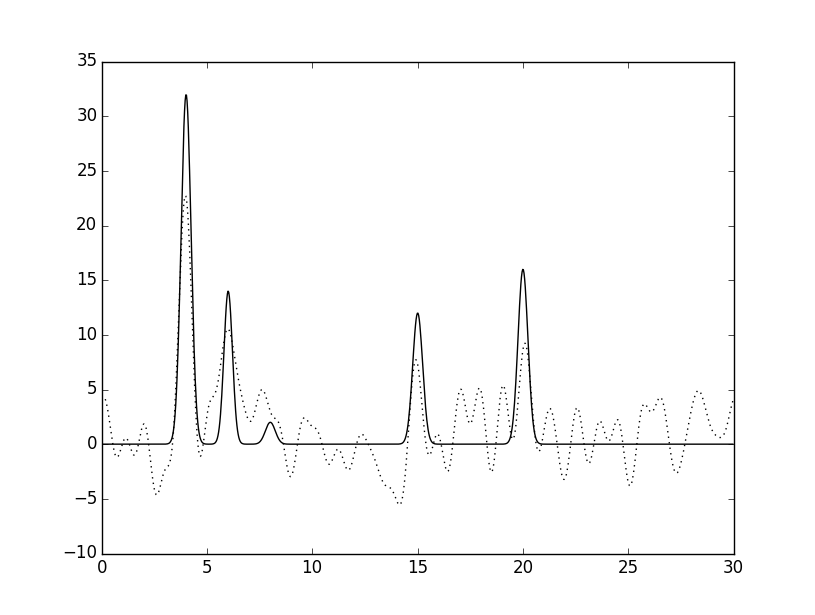 | 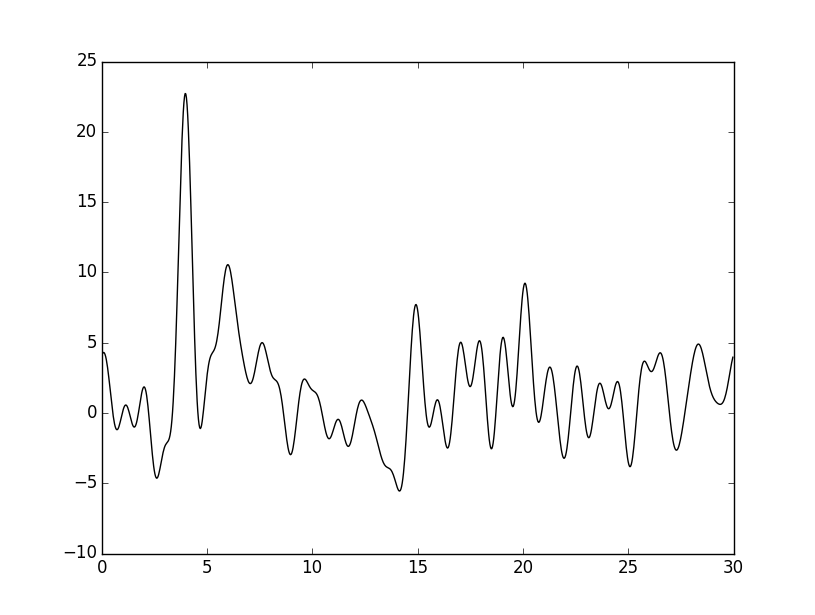 |
Сравнив рисунки 6 и 7, можно заметить, что при добавлении шума 10% по фазе, колебания графика увеличились сильнее,
чем при добавлении такого же шума по амплитуде. Однако атом водорода лучше угадывается на рисунке 6.
При шуме 10% восстановление можно считать "хорошим", при 15% - "средним", при 35% - "плохим".
3. Неполные наборы гармоник
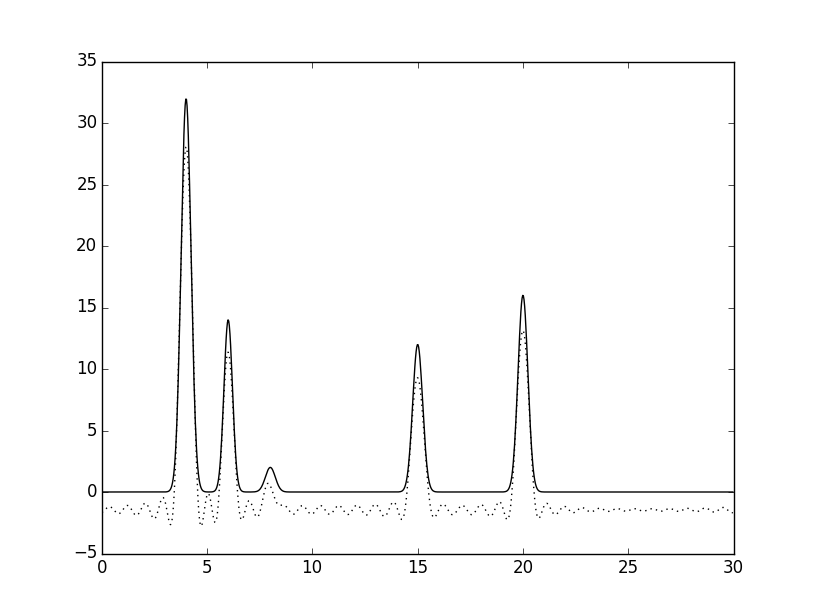
Для получения неполного набора сначала удалим 1) гармонику 0, 2) гармоники 0 и 1. Для этого используем скрипт fourier-filter.pyс параметром -r 1-34 или -r 2-34. Результаты восстановления приведены ниже.
 |
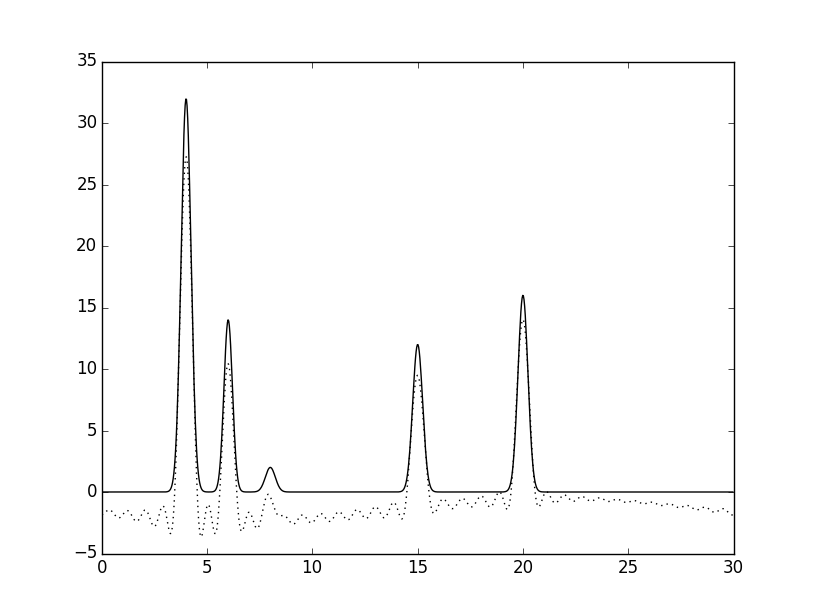 |
При исключении гармоники 0, график только смещается по вертикальной оси (гармоника 0 соответствует первому коэффициенту в ряду Фурье). При исключении двух первых гармоник функция искажается, но положения атомов по-прежнему четко определяются.
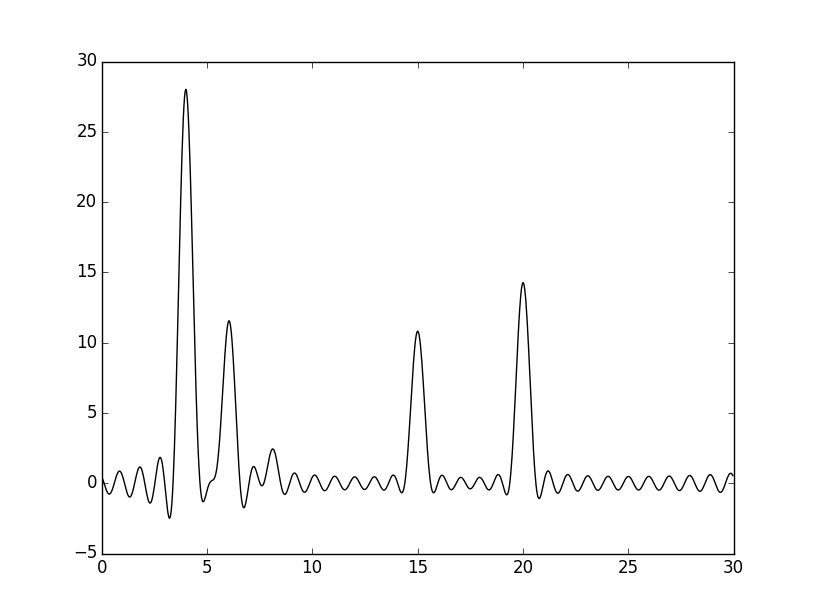
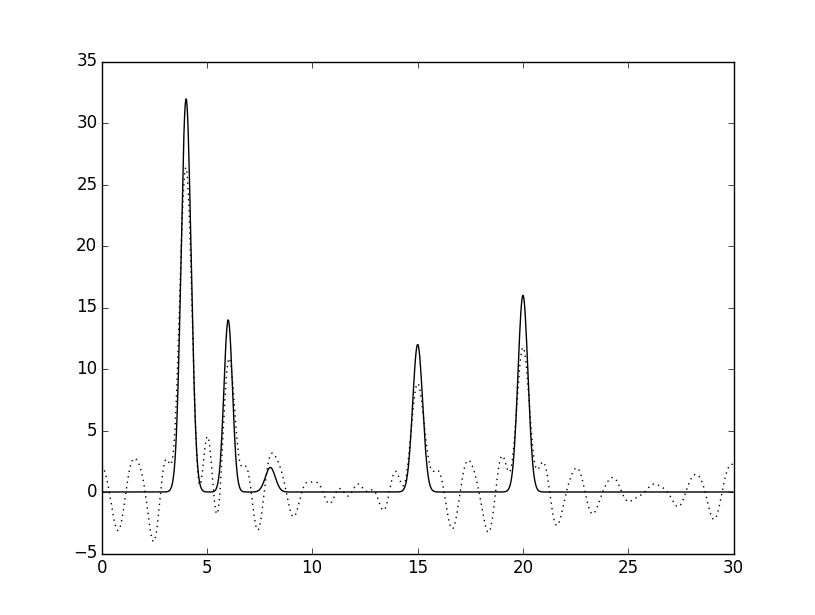
Теперь попробуем удалить 5-10% гармоник из середины набора: сначала удалим гармоники 17-19. Для этого используем fourier-filter.pyс параметром -r 0-16, 20-34. Результаты представлены ниже.
 |
Попробуем удалить побольше гармоник из середины, с 16 по 20.
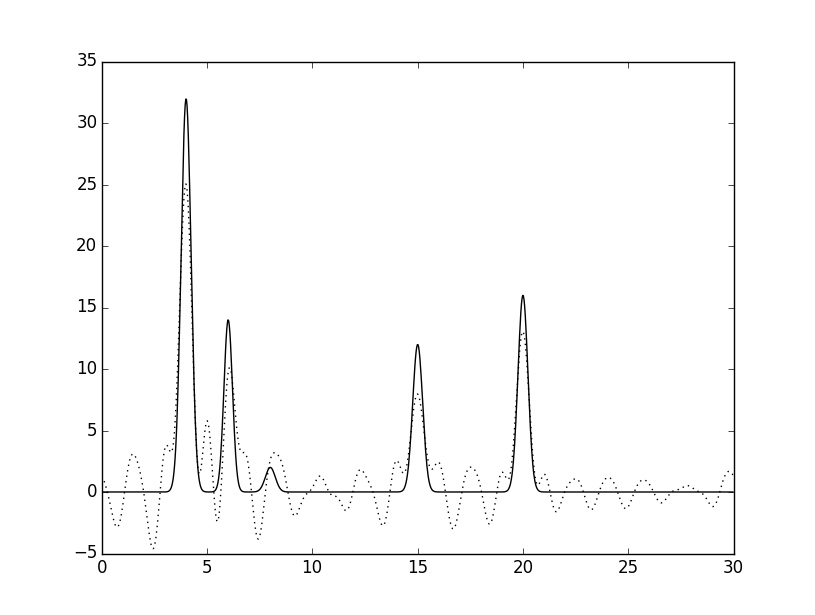 |
Получившиеся восстановления можно назвать "средними". Но чем больше гармоник удаляется из середины набора, тем сильнее максимумы от атомов похожи на шум - ниже качество восстановления.
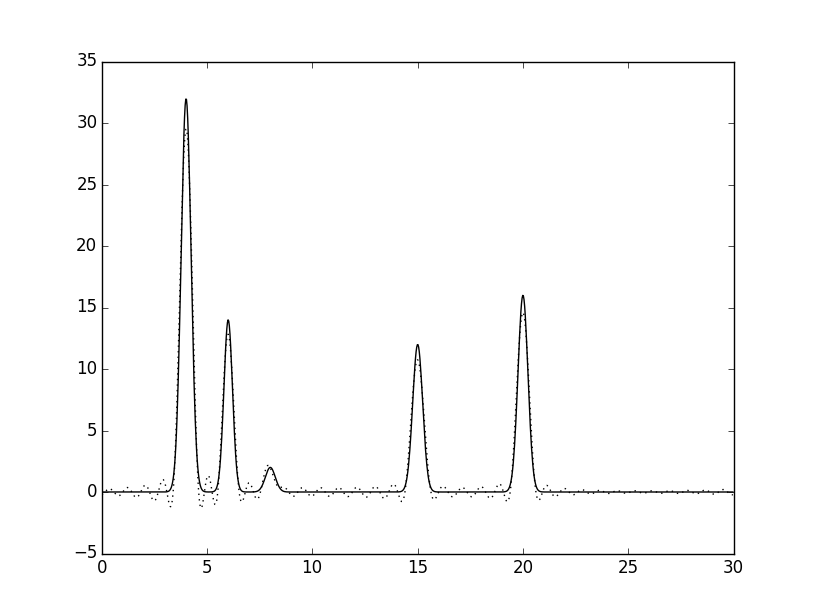
Теперь добавим одну гармонику с номером, превышающим n_0 на 10 - гармонику 44 (fourier-filter.py -r 0-34,44).
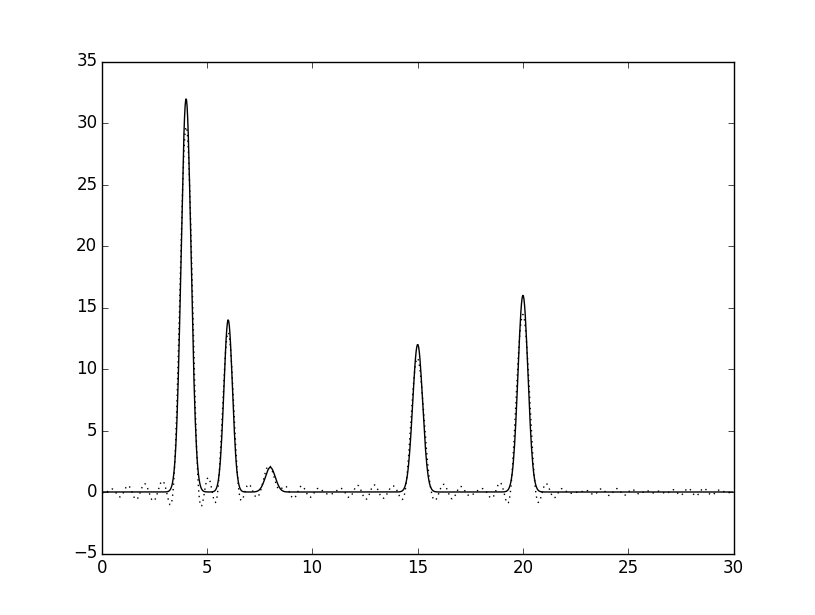 |  |
Значительных отличий от восстановления по полному набору 0,...,n_0 я не заметила, лишь слабо различимое увеличение шума.
Как определять разрешение для набора гармоник Фурье, по которым восстанавливается функция?
Разрешением полного набора гармоник называется период гармоники с наибольшим номером,
а период гармоники равен расстоянию между соседними максимумами синусоиды.
В моем случае разрешение (d=T/n) составит 30/34=0,88 Å.
Полнота данных определяется как процент присутствующих в наборе гармоник с длиной волны, большей d,
от максимально возможного при данном d числа гармоник. Для полного набора данных полнота равна 100%.
Для неполного набора нет строгого определения разрешения, кроме него необходимо также сообщать полноту данных.
Так, например, для набора (0-15)+(21-34) разрешение равно 0,88 Å при полноте данных 85,7%. Так же можно рассуждать и для набора (2-34).
Однако для того случая, когда рассматривается набор (0-34)+44, такая логика не совсем верна.
Выходит, что разрешение равно 0,67 Å при полноте данных 80%. Более рационально было бы не рассматривать гармонику 44
и считать разрешение равным 0,88 Å при полноте 100%, и хуже от этого не станет.
Т.е., при определении разрешения стоит обращать внимание на структуру набора, и при малой полноте иногда можно выкинуть единичные гармоники, по номеру далеко стоящие от непрерывного или почти непрерывного ряда.
Таблица 1 Восстановление функции по коэффициентам ряда Фурье
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум амплитуды (% от F) | Шум фазы (% от φ) | Качество восстановления | |
| Полный набор гармоник | ||||||
| 0-15 | 2 | 100 | 0 | 0 | среднее | |
| 0-25 | 1,2 | 100 | 0 | 0 | среднее | |
| 0-30 | 1 | 100 | 0 | 0 | хорошее | |
| 0-34 | 0,88 | 100 | 0 | 0 | отличное | |
| 0-34 | 0,88 | 100 | 10 | 0 | хорошее | |
| 0-34 | 0,88 | 100 | 0 | 10 | хорошее | |
| 0-34 | 0,88 | 100 | 15 | 15 | среднее | |
| 0-34 | 0,88 | 100 | 35 | 35 | плохое | |
| Неполный набор гармоник | ||||||
| 1-34 | 0,88 | 97 | 0 | 0 | отличное | |
| 2-34 | 0,88 | 94 | 0 | 0 | отличное | |
| (0-16)+(20-34) | 0,88 | 91 | 0 | 0 | среднее | |
| (0-15)+(21-34) | 0,88 | 85,7 | 0 | 0 | среднее | |
| (0-34)+44 | 0,88 | 100 | 0 | 0 | отличное | |