В биоинформатике метод присоединения соседей − восходящий кластерный метод для создания филогенетических деревьев, разработанный Наруя Сайтоу и Масатоши Ней в 1987 году [1]. Алгоритм обычно используется для деревьев, основанных на ДНК или белковых последовательностях, и требует знания расстояний между каждой парой таксонов (например, видов или последовательностей) для построения дерева.

Алгоритм

Метод присоединения соседей на вход принимает матрицу расстояний, задающую расстояния между каждой парой таксонов. Алгоритм начинает работу с полностью неразрешенного дерева с топологией "звезда", и выполняет итерации, состоящие из описанных далее шагов, до момента, когда дерево полностью разрешено и длины всех ветвей известны:

1.По текущей матрице расстояний считается Q-матрица (определенная ниже)

2.Ищется пара различных таксонов i и j, для которых значение Q(i,j) − наименьшее. Эти таксоны присоединяются к новому узлу, который, в свою очередь, соединяется с центральным узлом. На рисунке справа f и g присоединены к новому узлу u

3.Рассчитывается расстояние от каждого из присоединенных таксонов к новому узлу

4.Рассчитывается расстояние от каждого из оставшихся таксонов к новому узлу

5.Алгоритм запускается снова, заменяя пару присоединенных соседей на новый узел и используя расстояния, посчитанные на предыдущих шагах.

Q-матрица

Q-матрица рассчитывается по матрице расстояний между n таксонами следующим образом:

Расстояние между парой присоединенных соседей и новым узлом

Для каждого из присоединенных таксонов используется следующая формула для расчета расстояний до нового узла:

и

Таксоны f и g − пара присоединенных таксонов и u − новый узел. Ветви (f,u) и (g,u) и их длины delta (f,u) и delta (g,u) − теперь фиксированная часть дерева; они не изменятся и ни на что не повлияют на следующих шагах алгоритма.

Расстояние между оставшимися таксонами и новым узлом

Для каждого таксона, не участвовавшего в предыдущем шаге, рассчитывается расстояние до нового узла:

где u − новый узел, k − узел, до которого мы хотим рассчитать расстояние, f и g − таксоны только что присоединенной пары.

Реализация алгоритма без оптимизации имеет сложность n^3; существуют реализации, использующие эвристический подход с меньшим временем выполнения в среднем [2].

Jalview использует подсчет совпадаюющих букв, матрицу PAM 250 и матрицу BLOSUM62, результаты могут быть неточными при большом числе последовательностей в выравнивании, как нас предупреждают на сайте. Метод, основанный здесь на матрице PAM250 - это метод Дэйхофф.Эмпирические исследования аминокислотных замен позволили установить, что чаще происходят замены на сходные по физико- химическим свойствам аминокислоты (такие как полярность и объем бокового радикала). Другими словами, большинство аминокислотных замен не являются случайными, а обратные и параллельные замены чаще встречаются для сходных аминокислот.

Такие аминокислоты, как глицин, цистеин и триптофан заменяются редко, поэтому разные скорости замен в различных аминокислотных сайтах вызовут неточности в значениях РС-дистанций.

Для учета этого фактора Дэйхофф в 1978 г. предложила другой метод вычисления эволюционных дистанций, в котором используется матрица замен аминокислот для относительно короткого периода времени, а взаимосвязь между долей идентичных аминокислот и числом аминокислотных замен вычисляется эмпирически, исходя из данных по гемоглобинам, цитохрому с и фибринопептидам.

Первоначально создается эволюционное дерево для близкородственных аминокислотных последовательностей, а затем рассчитываются относительные частоты замен различных аминокислот. На основании этих данных создается эмпирическая матрица замещений 20 аминокислот.За единицу времени в матрице принято среднее время, за которое происходит одна замена аминокислоты в 100 сайтах. Дэйхофф предложила измерять количество замен аминокислот в РАМ (point accepted mutations, точечные зафиксированные мутации, 1 РАМ – 1 замена аминокислоты / 100 сайтов). Поэтому матрица замен аминокислот Дэйхофф часто называется РАМ-матрицей, на основании которой Дэйхофф предложила свою единицу скорости эволюции белка – число РАМов, накопившееся за 100 млн. лет. С помощью матрицы (M) Дэйхофф можно предсказывать эволюционные изменения аминокислот за любой период времени, если известна начальная аминокислотная последовательность.

Что использует MEGA и PHYLIP

1.Пуассон-корректированная дистанция. Одной из причин нелинейной зависимости р-дистанции от t является постепенное нарастание несоответствия nd и истинного числа замен аминокислот при множественных заменах в определенных сайтах. Для более точного определения числа замен следует использовать коррекцию Пуассона.

Обозначим скорость аминокислотных замен в год в определенном сайте как r и для упрощения предположим, что r во всех сайтах одинакова. Это предположение выполняется не всегда, но как будет показано дальше, вызванная им ошибка мала при малых значениях р. Пусть rt – это среднее число аминокислотных замен на сайт за период времени t, а вероятность (Р) возникновения количества k аминокислотных замен в сайте (k = 0, 1, 2, 3,…) следует распределению Пуассона. Тогда P(k;t) = (rt)^k)*(e^(-rt))/k. И тогда вероятность отсутствия аминокислотных замен в сайте определяется как P (0; t) = e^(-rt), Число аминокислотных замен оценивается при сравнении двух гомологичных последовательностей, которые дивергировали t лет назад. Так как вероятность отсутствия замены в аминокислотном сайте последовательности определяется как e^(–rt), то вероятность, что ни в одном из гомологичных сайтов двух последовательностей не произойдет замены (q) равна: q = (e(–rt))^2 = e^(–2rt).

Таким образом, получаем, что общее число аминокислотных замен на сайт для двух последовательностей (d = 2rt) определяется как: d = – ln (1 – p).

2.Дистанция Кимуры. Эволюционная дистанция Кимуры (Каа, dK) представляет собой еще один вариант коррекции р-дистанции. Ее вычисление производится по эмпирической формуле, полученной путем преобразования соотношения, указанного в предыдущем пункте dK = – ln (1 – р – 1/5р^2)

3.Гамма-дистанция и дистанция Гришина. Все рассмотренные выше методы определения эволюционных дистанций основаны на предположении о равной скорости замен в различных аминокислотных сайтах. На практике это предположение часто оказывается некорректным, так как скорость замен в функционально важных сайтах низкая. В 1971 г. Азл и Корбин показали, что количество аминокислотных замен на сайт имеет большую вариансу, чем Пуассонова варианса, и этот показатель приблизительно следует отрицательному биноминальному распределению. Если скорость аминокислотных замен на сайт варьирует в соответствии с гамма распределением, то наблюдаемое число замен на сайт следует отрицательному биноминальному распределению. Таким образом, скорость замен в сайтах варьирует в соответствии с гамма распределением и расстояние выводится из него.

Я построила деревья методом neighbor-joining в Jalview, MEGA и UGENE (пакет PHYLIP).

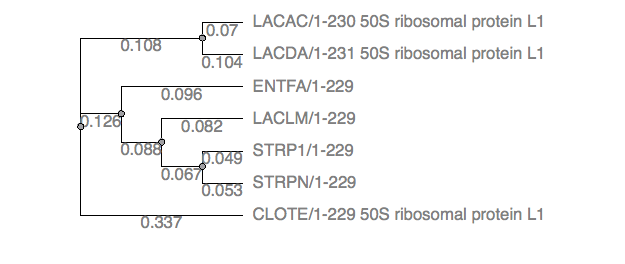
Реконструкция филогенетического древа NJ в UGENE

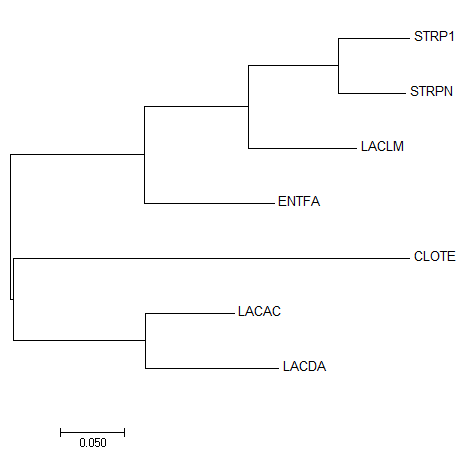
Реконструкция филогенетического древа NJ в MEGA (без бутстрепа)

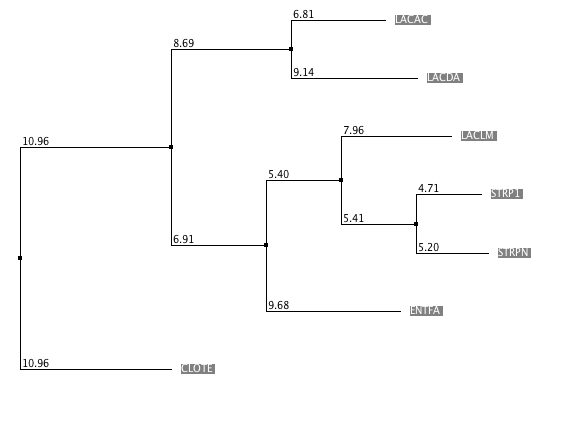
Реконструкция филогенетического древа NJ в Jalview (Neighbor-joining using % Identity)

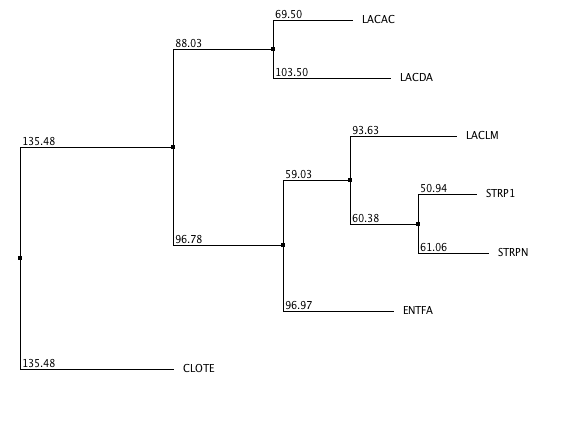
Реконструкция филогенетического древа NJ в Jalview (Neighbor-joining using BLOSUM62)

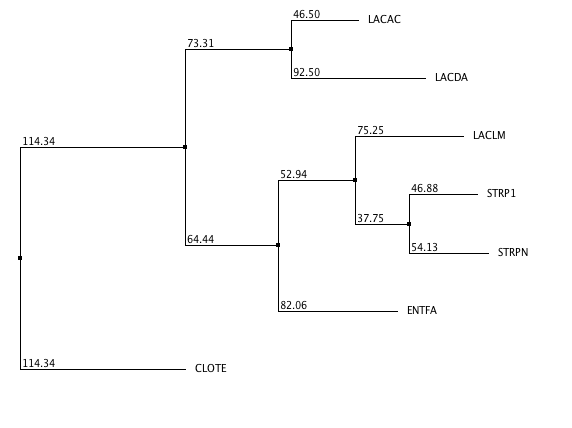
Реконструкция филогенетического древа NJ в Jalview (Neighbor-joining using PAM 250)

MEGA (без бутстрепа) и Jalview:

1.Ветвь CLOTE имеет очень слабую поддержку в древе MEGA, а остальные ветви в целом совпадают

UGENE и Jalview:

1.Также поддержка ветви CLOTE очень слабая

MEGA (без бутстрепа) и UGENE:

1.Результаты обеих программ почти идентичны

Общий вывод:

>Результаты примерно одинаковые (даже среди трех вариатнов NJ в Jalview топология одинаковая), однако поддержка ветвей почти везде довольно сильно отличается. Так как древо видов составлено только по топологии, других отличий и свидетельств того, что в моем случае один алгоритм работает лучше другого, нет. На основе данных о поддержке ветвей в 3 вариантах NJ Jalview наиболее похож на древо из MEGA оказывается построенное на матрице PAM250.

*Кроме NJ я использовала Randomized Axelerated Maximum Likelihood (RAxML), что описано на страничке первого практикума.

Ссылки:

[1] Saitou N, Nei M. "The neighbor-joining method: a new method for reconstructing phylogenetic trees." Molecular Biology and Evolution, volume 4, issue 4, pp. 406-425, July 1987.

[2] Neighbour-joining tutorial URL// http://www.deduveinstitute.be/~opperd/private/neighbor.html

[3] Белорусский государственный медицинский университет "Методы молекулярной филогении" URL// http://biology.bsmu.by/files/biology_pdf/mol_metod/gl_1.pdf