Восстановления функции ЭП от одной переменной в зависимости от качества и количества используемых гармоник ряда Фурье.

Задание функции и восстановление ЭП по амплитудам и фазам

В работе использовался ряд скриптов. С помощью скрипта compile-func.py была задана функция по следующим параметрам: g 30,3,3+40,3,4.3+2,3.5,6.5+30,3,7.5 (сумма четырех гауссовых функций: их max в точках 3,4.3,6.5,7.5, высота 30,40,2,30 соответственно; ширина "колокола" порядка 1; третий - низкий - пик моделирует атом водорода). В результате был получен график, представленный на рисунке ниже.

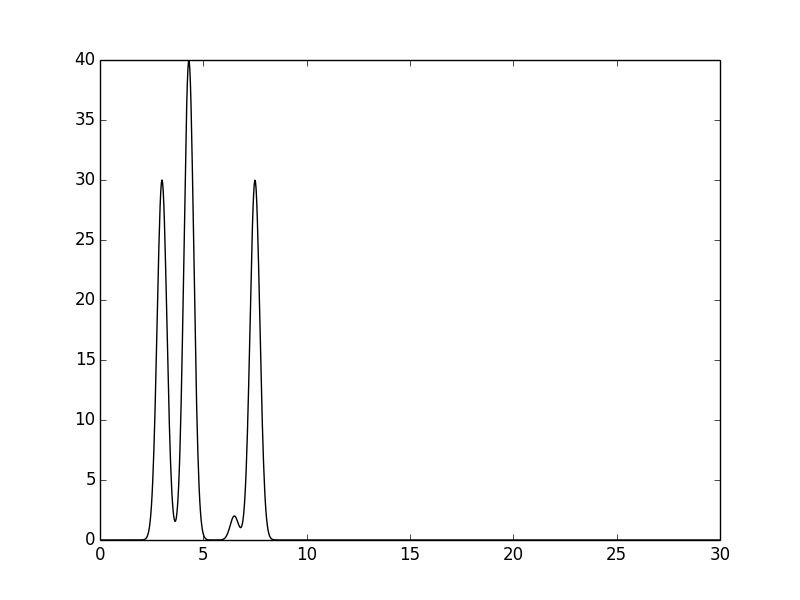Рис.1 Функция Гаусса.

Далее использовались скрипты func2fourier.py (для расчета коэффициентов Фурье) и fourier-filter.py для отбора гармоник. Целью было найти наилучшее восстановление функции. Рассматривались 6 интервалов (первые 10 гармоник, 20, 30, 40 и 50). Изображения представлены ниже, пунктиром показана исходная функция. Только после 30 гармоник можно однозначно определить количество молекул в ячейке и количестве атомов в молекуле.
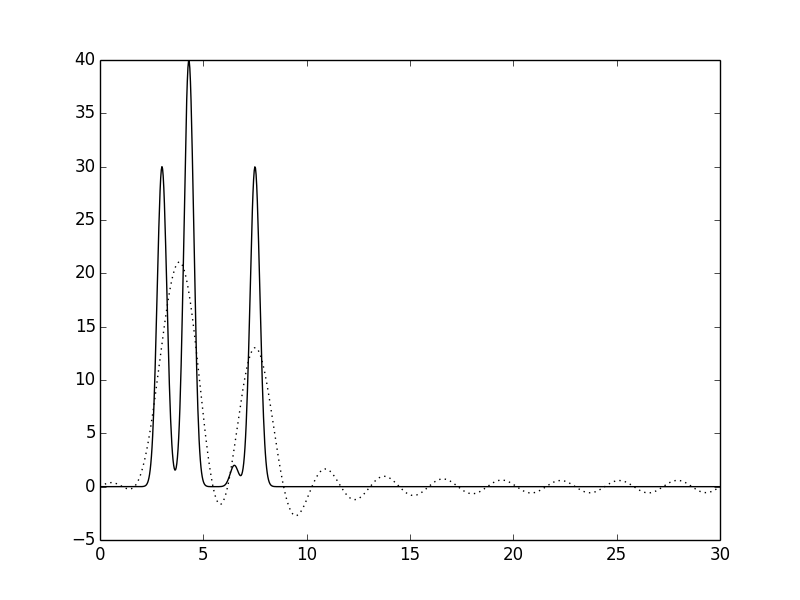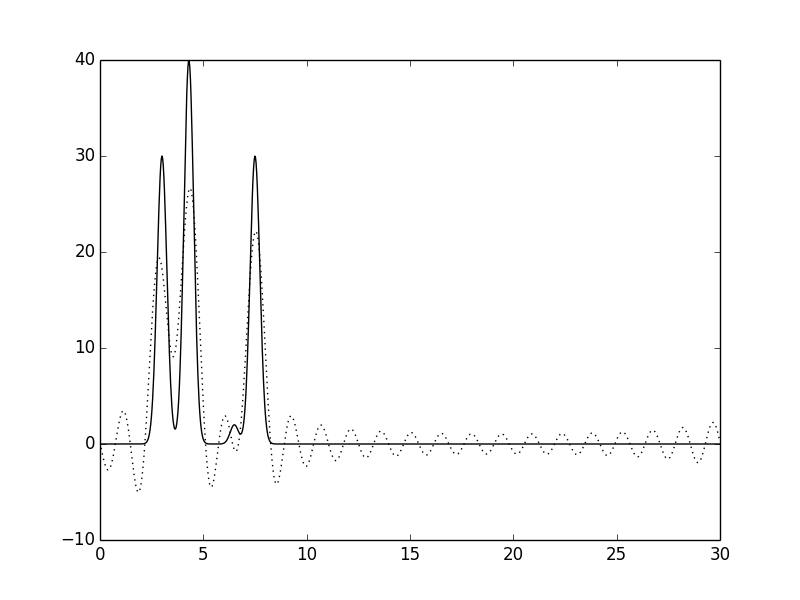Рис.2 Функции ЭП, восстановленные по первым 10 гармоникам.	Рис.3 Функции ЭП, восстановленные по первым 20 гармоникам.
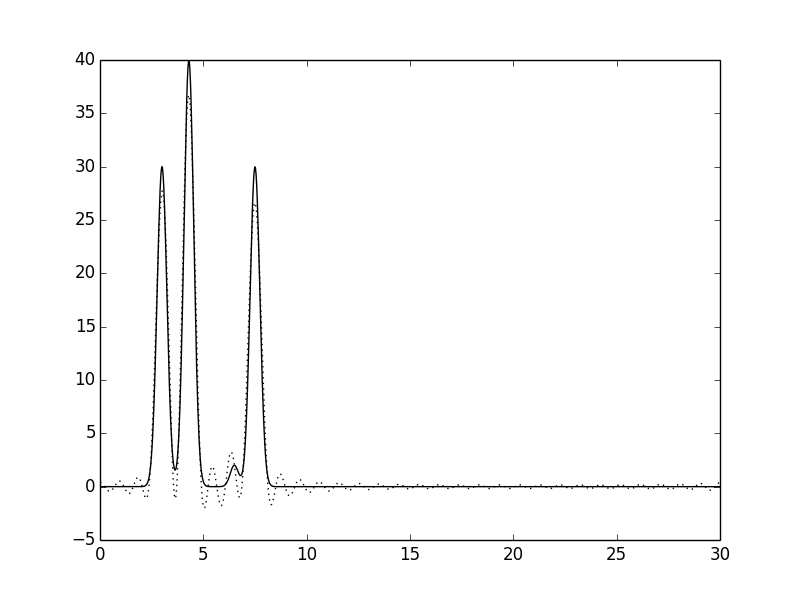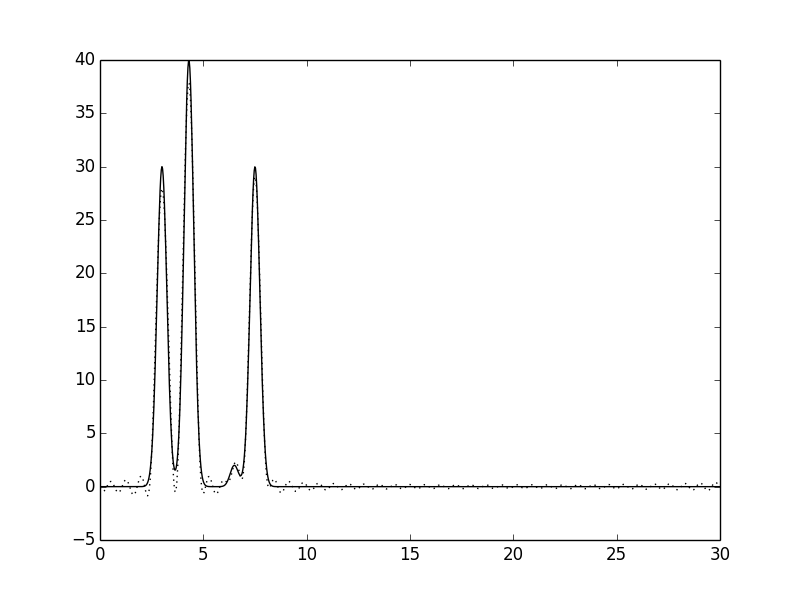Рис.4 Функции ЭП, восстановленные по первым 30 гармоникам.	Рис.5 Функции ЭП, восстановленные по первым 40 гармоникам.
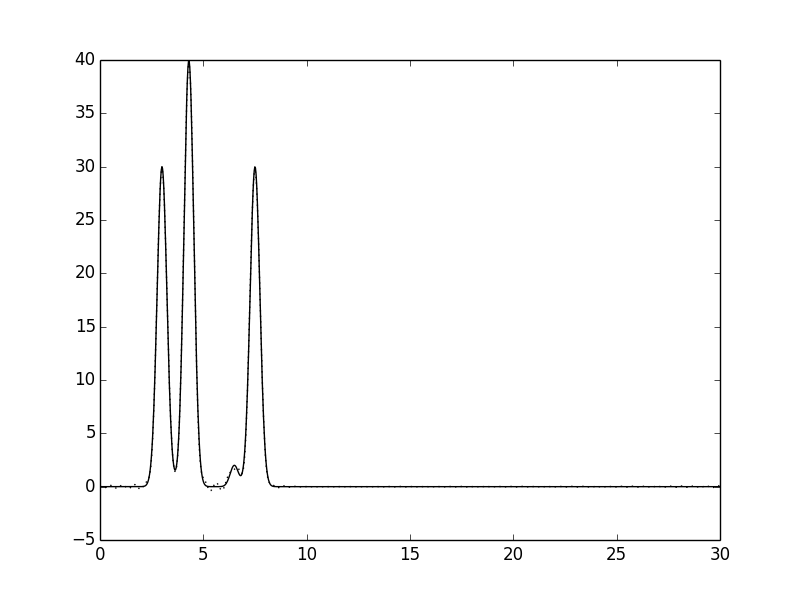Рис.6 Функции ЭП, восстановленные по первым 50 гармоникам.

Восстановление функции ЭП по амплитудам и фазам части сигналов

Далее работа проводилась на первых 50 гармониках (можно было остановиться и на 30, потому что уже на этом наборе гармоник получаются точные данные). К амплитудам и фазам добавлялся шум в размере 25%. При таком количестве шума удается установить положение атомов. Полученные графики представлены ниже, пунктиром показана исходная функция.

Рис.7 Функции ЭП, восстановленные по данным с 25% шумом, добавленным к амплитудам.

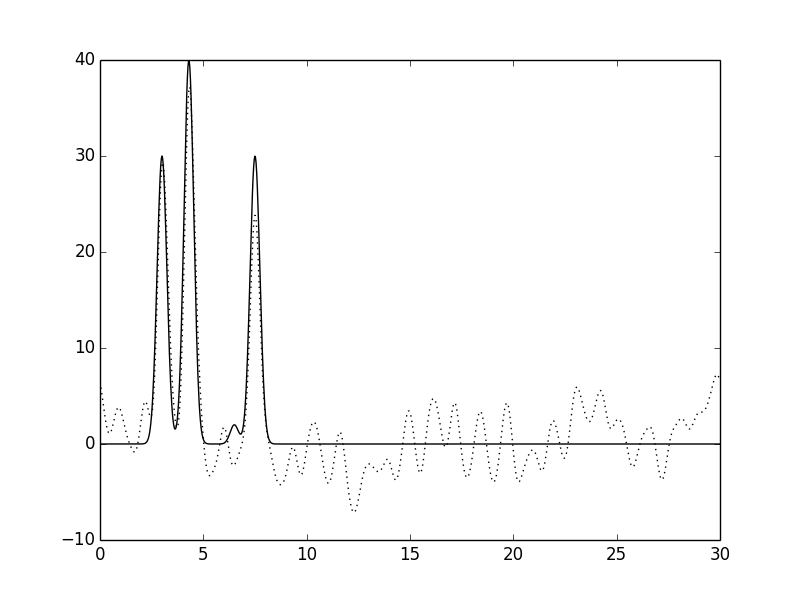Рис.8 Функции ЭП, восстановленные по данным с 25% шумом, добавленным к фазам.

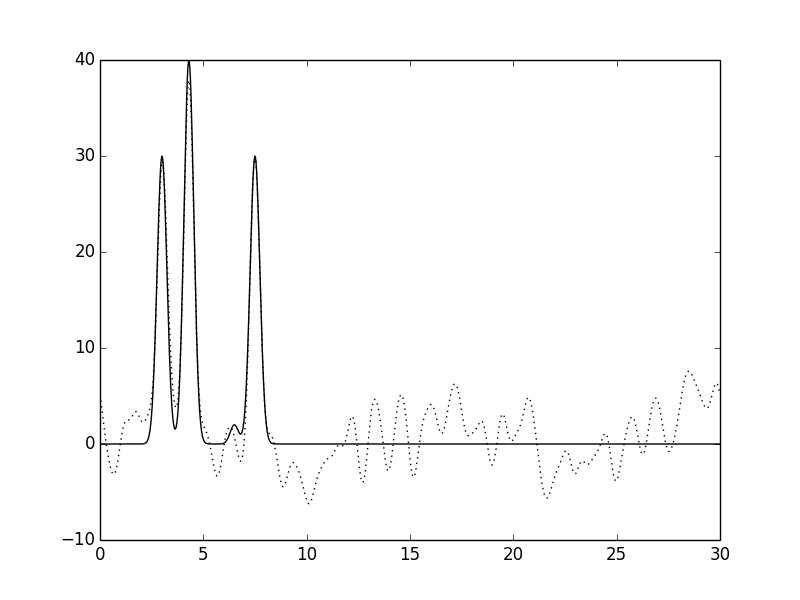Рис.9 Функции ЭП, восстановленные по данным с 25% шумом, добавленным к фазам и амплитудам.

Восстановление функций по неполным наборам гармоник
Далее проводилось восстановление функции по неполным наборам гармоник. Было рассмотрена 4 интервала: 0-10, 10-20, 20-30, 30-40. Результаты представлены ниже. В таблице представлены результаты по качеству рассмотренных гармоник.
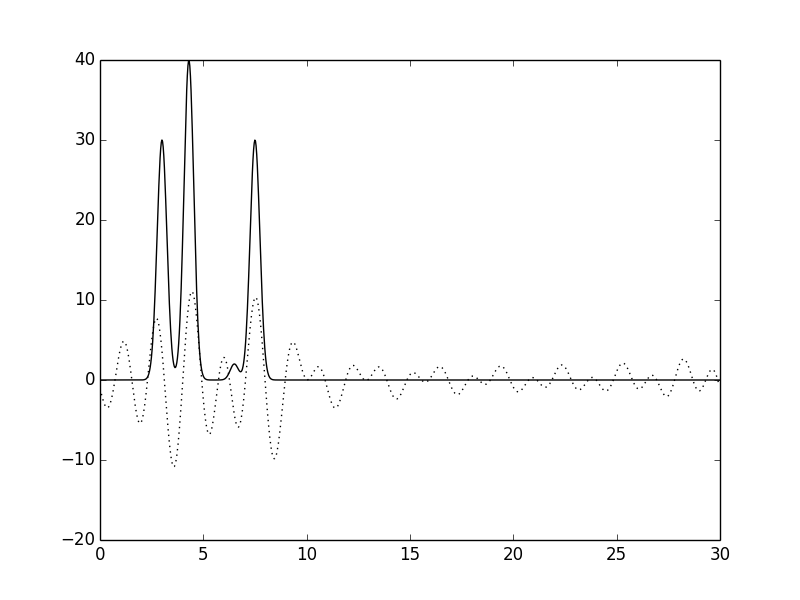Рис.10 Функции ЭП, восстановленные по первым 10 гармоникам.	Рис.11 Функции ЭП, восстановленные по гармоникам от 10 до 20.
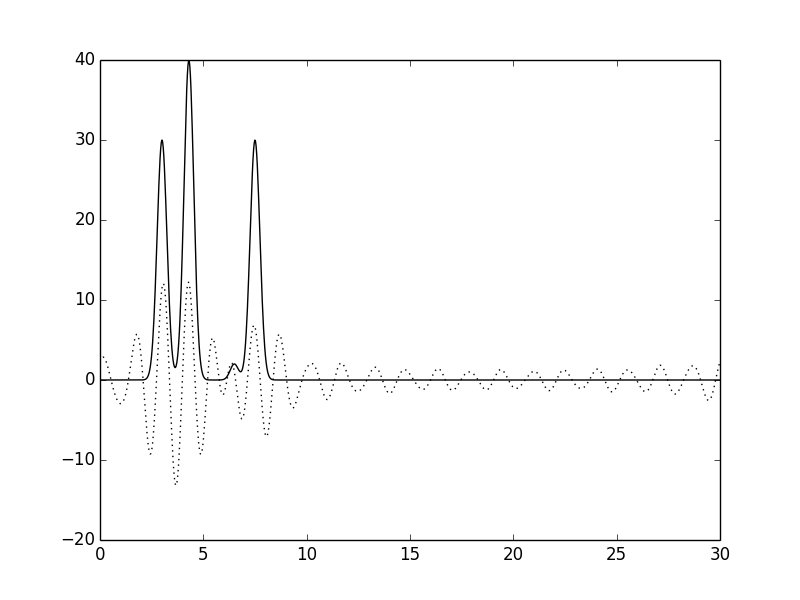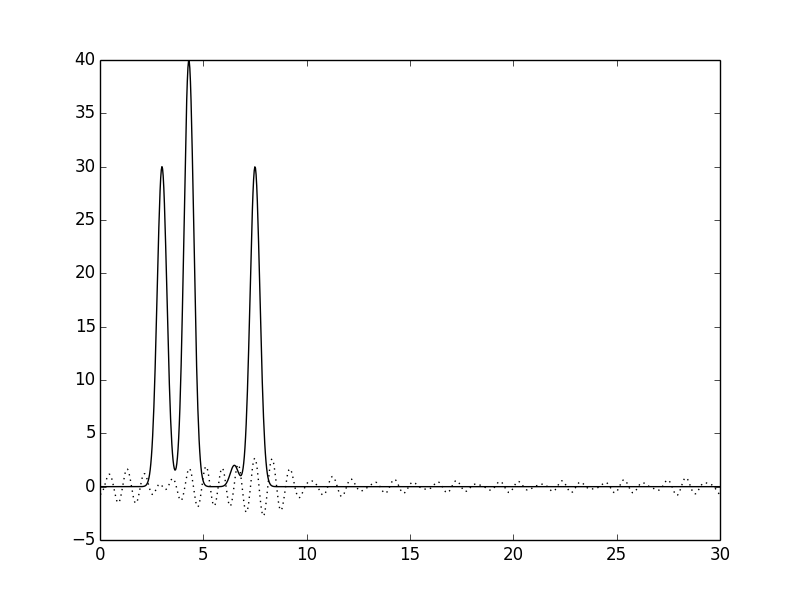Рис.12 Функции ЭП, восстановленные по гармоникам от 20 до 30.	Рис.13 Функции ЭП, восстановленные по гармоникам от 30 до 40.