Модель для компьютерного эксперимента: две молекулы (всего 5 атомов) расположены на расстоянии ~ 5 Å на отрезке [0, 30]. Электронные плотности атомов описываются гауссовой кривой. Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py:
compile-func.py -g 15,3.5,3.8+25,3.5,5.3+35,3.5,7.5+40,3,9.5+50,3,2
Выходной файл скрипта compile-func.py - текстовый файл func.txt, в котором описана заданная функция (в виде пар X – Y). Скрипт также позволяет получить изображение заданной совокупности гауссовых функций:
Коэффициенты разложения функции в ряд Фурье были получены с помощью скрипта func2fourier.py:
func2fourier.py -i func.txt -o first_output.txt
Выходной файл скрипта func2fourier.py – текстовый файл first_output.txt. В нём приведены 3 колонки: номер гармоники, амплитуда и фаза.
Всего было получено 499 гармоник. Необходимо найти n0, для которого по графику функции, восстановленной по набору гармоник 0, 1, ..., n0 можно определить положение максимумов всех гауссовых слагаемых («отличное восстановление»).
fourier-filter.py -r 0-1 -i first_output.txt -o 1_0-1.txt fourier2func.py -f func.txt -i 1_0-1.txt -o 2_0-1.txt fourier-filter.py -r 0-10 -i first_output.txt -o 1_0-10.txt fourier2func.py -f func.txt -i 1_0-10.txt -o 2_0-10.txt fourier-filter.py -r 0-20 -i first_output.txt -o 1_0-20.txt fourier2func.py -f func.txt -i 1_0-20.txt -o 3_0-20.txt fourier-filter.py -r 0-30 -i first_output.txt -o 1_0-30.txt fourier2func.py -f func.txt -i 1_0-30.txt -o 4_0-30.txt fourier-filter.py -r 0-40 -i first_output.txt -o 1_0-40.txt fourier2func.py -f func.txt -i 1_0-40.txt -o 5_0-40.txt fourier-filter.py -r 0-60 -i first_output.txt -o 1_0-60.txt fourier2func.py -f func.txt -i 1_0-60.txt -o 6_0-60.txt
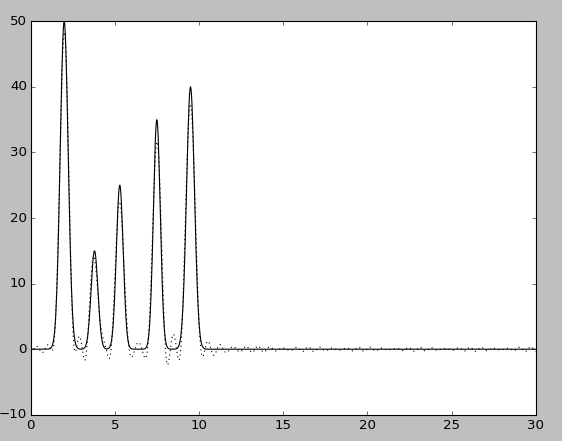
Значение n0 было определено равным 40. Ниже приведены графики восстановленных функций по полным наборам гармоник для n, равных 1,10,20,30,60 и n0 = 40 (крупные картинки доступны по щелчку, пунктирной линией указана восстановленная функция, сплошной - исходная).
На основании полученных рисунков значение n0 было определено равным 40.
Восстановление для n = 1, n = 10 можно оценить как «плохое»: положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".
Для n = 20 можно оценить как «среднее»: положение лишь некоторых атомов можно определить по восстановленной функции. Для n = 30 по восстановленной функции можно угадать положение всех максимумов, зная число слагаемых, однако на восстановленной функции максимумы некоторых «атомов» плохо отличимы от шума («хорошее восстановление»). По графику функции, восстановленной по полному набору гармоник 0, 1, ..., 40
можно определить положение максимума всех гауссовых слагаемых функции («отличное восстановление»). Использование больших значений n для полных наборов гармоник позволяет ещё более точно восстановить исходную функцию (n = 60)
Затем к амплитудам и фазам был добавлен шум (20% к амплитуде; 20% к фазе; по 10% к амплитуде и фазе):
# Добавление шума только к амплитуде func2fourier.py -F 20 -i func.txt -o func_noise20-0.txt fourier-filter.py -r 0-40 -i func_noise20-0.txt -o func_noise20-0_40.txt fourier2func.py -i func_noise20-0_40.txt -o 2_func_noise20-0_40.txt # Добавление шума только к фазе func2fourier.py -P 20 -i func.txt -o a_noise0-20.txt fourier-filter.py -r 0-40 -i a_noise0-20.txt -o a_noise20-0_40.txt fourier2func.py -i a_noise20-0_40.txt -o 2a_func_noise20-0_40.txt # Добавление шума к амплитуде и к фазе func2fourier.py -F 10 -P 10 -i func.txt -o fa_noise10-10.txt fourier-filter.py -r 0-40 -i fa_noise10-10.txt -o fa_noise10-10_0-40.txt fourier2func.py -i fa_noise10-10_0-40.txt -o 2fa_func_noise10-10_0-40.txt
Восстановление функции производилось по полному набору гармоник 0, 1, ..., n0. Качество восстановления заметно снизилось (можно охарактеризовать его как «среднее»), что отражено на изображениях ниже. На рисунках 8-10 представлены полученные графики (крупные картинки доступны по щелчку, пунктирной линией указана восстановленная функция, сплошной - исходная).
Для получения неполного набора гармоник были удалены одна и две начальные гармоники (гармоника с номером 0; гармоники с номерами 0 и 1):
# Удаление первой гармоники fourier-filter.py -r 1-40 -i first_output.txt -o f_1-40.txt fourier2func.py -i f_1-40.txt -o 1-40.txt # Удаление первых двух гармоник fourier-filter.py -r 2-40 -i first_output.txt -o f_2-40.txt fourier2func.py -i f_2-40.txt -o 2-40.txt
В случае удаления первой гармоники при последующем восстановлении функции видно, что она смещена по оси ординат; при этом восстановление остается «отличным». Это ожидаемый результат, так как значение первой гармоники равно числу F0 – первому коэффициенту ряда Фурье.
В результате удаления первых двух гармоник восстановленная функция заметно искажается, однако значения максимумов можно однозначно определить.
Полученные графики функций представлены на рисунках 11-12 (крупные картинки доступны по щелчку, пунктирной линией указана восстановленная функция, сплошной - исходная).
Для получения неполного набора гармоник без ~5%-10% гармоник в середине были удалены гармоники с номерами 29 , 30 (5%); гармоники с номерами 21 - 24(10%):
# Удаление 5% гармоник в середине набора fourier-filter.py -r 0-28,31-40 -i first_output.txt -o 0-28_31-40.txt fourier2func.py -i 0-28_31-40.txt -o 29-30del.txt # Удаление 10% гармоник в середине набора fourier-filter.py -r 0-20,25-40 -i first_output.txt -o 0-20_25-40.txt fourier2func.py -i 0-20_25-40.txt -o del21-25.txt
Удаление как 10%, так и 5% гармоник в середине набора привело к ухудшению качества восстановления (его можно охарактеризовать как что-то между «средним» и «хорошим» ). Таким образом, вследствие удаления гармоник в середине набора максимумы от «атомов» становятся менее отличимы от шума. Полученные графики функций представлены на рисунках 13, 14 (крупные картинки доступны по щелчку, пунктирной линией указана восстановленная функция, сплошной - исходная).
К набору гармоник 0, 1, ..., 40 была добавлена гармоника 50:
fourier-filter.py -r 0-40,50 -i first_output.txt -o 0-40_50.txt fourier2func.py -i 0-40_50.txt -o v.txt
Добавление гармоники с номером n0+10 к набору гармоник 0, 1, ..., n0, насколько можно судить по изображению восстановленной функции, не изменила качество восстановления. При сравнении с функцией, восстановленной по набору гармоник 0, 1, ..., n0, удаётся обнаружить лишь незначительные изменения
Для полного набора гармоник разрешение определяется как период гармоники с наибольшим номером. Тогда, например, разрешение для полного набора гармоник 0, 1, ..., 40 равно 30 A / 40 ≈ 0,75 A (в данном компьютерном эксперименте). Полнота данных вычисляется как процент гармоник в наборе, период которых не меньше разрешения, от числа гармоник в полном наборе для этого разрешения. Для полного набора полнота данных равна 100%.
Для неполного набора гармоник разумно всегда указывать, помимо разрешения, полноту данных. Так, для набора гармоник 0, 1, ..., 40, 50 разрешение можно определить равным ~0,60 A при полноте данных 80%. Однако более «справедливым» выглядит разрешение ~0,75 A при полноте данных 100%. Таким образом, при указании разрешения для неполного набора гармоник видится разумным использование некоего условного порога на полноту данных (например, в 90%).
| Набор гармоник | Разрешение, A | Полнота данных, % | Шум амплитуды (% от F) | Шум фазы (% от phi) | Качество восстановления |
| Полный набор гармоник | |||||
| 0-1 | 30 | 100 | 0 | 0 | Плохое |
| 0-10 | 3 | 100 | 0 | 0 | Плохое |
| 0-20 | 1.5 | 100 | 0 | 0 | Среднее |
| 0-30 | 1 | 100 | 0 | 0 | Хорошее |
| 0-40 | 0,75 | 100 | 20 | 0 | Среднее |
| 0-40 | 0,75 | 100 | 0 | 20 | Среднее |
| 0-40 | 0,75 | 100 | 10 | 10 | Среднее |
| 0-40 | 0,75 | 100 | 0 | 0 | Отличное |
| Неполный набор гармоник | |||||
| 1-40 | 0,75 | 97,5 | 0 | 0 | Отличное |
| 2-40 | 0,75 | 95 | 0 | 0 | Отличное |
| 0-28, 31-40 | 0,75 | 95 | 0 | 0 | Хорошее |
| 0-20, 25-40 | 0,75 | 90 | 0 | 0 | Хорошее |
| 0-40, 50 | 0,75 | 100 | 0 | 0 | Отличное |